Students can use the Spectrum Math Grade 3 Answer Key Chapter 6 Pretest as a quick guide to resolve any of their doubts.
Spectrum Math Grade 3 Chapter 6 Pretest Answers Key
Check What You Know
What fraction of each figure is shaded?
Question 1.
a.
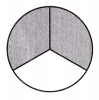
Answer: The shaded area in a fraction is \(\frac{2}{3}\).
Explanation: Given the circle figure,
Now, we will write the shaded region values in fractions.
The given circle has 3 parts. In this, two of the parts are shaded.
So, the shaded set value in fractions is \(\frac{2}{3}\).
b.

Answer: The shaded area in a fraction is \(\frac{1}{4}\).
Explanation: Given the square figure,
Now, we will write the shaded region values in fractions.
The given squares have 4 square parts. In this, one of the squares is shaded.
So, the shaded set value in fractions is \(\frac{1}{4}\).
c.
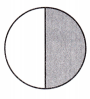
Answer: The shaded area in a fraction is \(\frac{1}{2}\).
Explanation: Given the circle figure,
Now, we will write the shaded region values in fractions.
The given circle has 2 parts. In this, one of the parts is shaded.
So, the shaded set value in fractions is \(\frac{1}{2}\).
Question 2.
a.
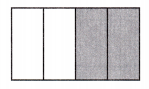
Answer: The shaded area in a fraction is \(\frac{2}{4}\).
Explanation: Given the rectangle figure,
Now, we will write the shaded region values in fractions.
The given rectangle has 4 square parts. In this, two of the parts are shaded.
So, the shaded set value in fractions is \(\frac{2}{4}\).
b.
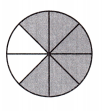
Answer: The shaded area in a fraction is \(\frac{6}{8}\).
Explanation: Given the circle figure,
Now, we will write the shaded region values in fractions.
The given circle has 8 parts. In this, 6 of the parts are shaded.
So, the shaded set value in fractions is \(\frac{6}{8}\).
c.
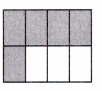
Answer: The shaded area in a fraction is \(\frac{5}{8}\).
Explanation: Given the square figure,
Now, we will write the shaded region values in fractions.
The given squares have 8 square parts. In this, five of the parts are shaded.
So, the shaded set value in fractions is \(\frac{5}{8}\).
What fraction of each set is shaded?
Question 3.
a.

Answer: The shaded area in a fraction is \(\frac{1}{2}\).
Explanation: Given the circle figure set,
Now, we will write the shaded region values in fractions.
The given circle set has 2 circles. In this, one of the circles is shaded.
So, the shaded set value in fractions is \(\frac{1}{2}\).
b.

Answer: The shaded area in a fraction is \(\frac{1}{4}\).
Explanation: Given the square figure set,
Now, we will write the shaded region values in fractions.
The given square set has 4 squares. In this, one of the squares is shaded.
So, the shaded set value in fractions is \(\frac{1}{4}\).
c.

Answer: The shaded area in a fraction is \(\frac{3}{4}\).
Explanation: Given the triangle figure,
Now, we will write the shaded region values in fractions.
The given triangle set has 4 triangles. In this, three of the triangles are shaded.
So, the shaded set value in fractions is \(\frac{3}{4}\).
Question 4.
Label these fractions on the number line: \(\frac{1}{6}\) and \(\frac{4}{6}\)

Answer: The \(\frac{1}{6}\), \(\frac{4}{6}\) is labelled on line is shown below,

Explanation: Given the value is \(\frac{1}{6}\), \(\frac{4}{6}\),
Now, we will label the given value on a line.
The steps for labeling a line are below,
1. First, divide the number line into 6 equal parts (the denominator).
2. Next, count from zero the parts you need (the numerator). The parts are \(\frac{1}{6}\), \(\frac{2}{6}\), \(\frac{3}{6}\), \(\frac{4}{6}\), \(\frac{5}{6}\), \(\frac{6}{6}\),
3. Now, we can label the fraction of \(\frac{1}{6}\), \(\frac{4}{6}\), in a given line.

Use >, <, or = to compare the fractions.
Question 5.
a.
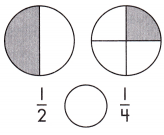
Answer: \(\frac{1}{2}\) >\(\frac{1}{4}\)
Explanation: Given the two circle figures with fraction values.
Now, we will compare the given fraction value.
So, the values are \(\frac{1}{2}\),\(\frac{1}{4}\).
i.e., \(\frac{1}{2}\) >\(\frac{1}{4}\).
Therefore, \(\frac{1}{2}\) is greater than \(\frac{1}{4}\).
b.
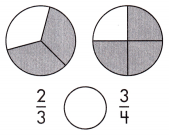
Answer: \(\frac{2}{3}\)< \(\frac{3}{4}\)
Explanation: Given the two circle figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{2}{3}\), \(\frac{3}{4}\).
i.e., \(\frac{2}{3}\) < \(\frac{3}{4}\).
Therefore, \(\frac{2}{3}\) is less than \(\frac{3}{4}\).
c.
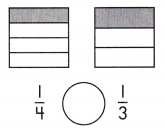
Answer: \(\frac{1}{4}\) < \(\frac{1}{3}\)
Explanation: Given the two rectangle figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{1}{4}\),\(\frac{1}{3}\).
i.e., \(\frac{1}{4}\)< \(\frac{1}{3}\).
Therefore, \(\frac{1}{4}\) is less than \(\frac{1}{3}\).
What fraction of each figure is shaded? Compare the fractions. Use >, <, or =.
Question 6.
a.
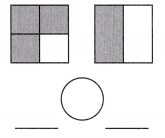
Answer: The given figure value in fractions is \(\frac{3}{4}\) \(\frac{1}{2}\)
\(\frac{3}{4}\) >\(\frac{1}{2}\).
Explanation: Given the two square figures.
Now, we will find the given figures’ values in fractions and find which is the greater, lesser, and equal value.
So, the given figure value in fractions is \(\frac{3}{4}\), \(\frac{1}{2}\).
Then in these values, the value \(\frac{1}{2}\) is lesser.
i.e., \(\frac{3}{4}\) >\(\frac{1}{2}\).
b.
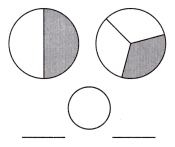
Answer: The given figure value in fractions is \(\frac{1}{2}\) \(\frac{1}{3}\)
\(\frac{1}{2}\) > \(\frac{1}{3}\).
Explanation: Given the two circle figures.
Now, we will find the given figures’ values in fractions and find which is the greater, lesser, and equal value.
So, the given figure value in fractions is \(\frac{1}{2}\), \(\frac{1}{3}\).
Then in these values, the value \(\frac{1}{3}\) is lesser.
i.e., \(\frac{1}{2}\)>\(\frac{1}{3}\).
c.

Answer: The given figure value in fractions is \(\frac{1}{2}\) \(\frac{2}{4}\)
\(\frac{1}{2}\) = \(\frac{2}{4}\).
Explanation: Given the two square figures.
Now, we will find the given figures’ values in fractions and find which value is the greater, lesser, and equal.
So, the given figure value in fractions is \(\frac{1}{2}\), \(\frac{2}{4}\).
Then in these values, both are equal.
i.e., \(\frac{1}{2}\)= \(\frac{2}{4}\).
Label the following on the number line.
Question 7.
\(\frac{3}{8}\) and \(\frac{8}{8}\)

Answer: The \(\frac{3}{8}\), \(\frac{8}{8}\) is labelled on line is shown below,

Explanation: Given the value is \(\frac{3}{8}\), \(\frac{8}{8}\),
Now, we will label the given value on a line.
The steps for labeling a line are below,
1. First, divide the number line into 8 equal parts (the denominator).
2. Next, count from zero the parts you need (the numerator). The parts are \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\), \(\frac{4}{8}\), \(\frac{5}{8}\), \(\frac{6}{8}\), \(\frac{7}{8}\), \(\frac{8}{8}\),
3. Now, we can label the fraction of \(\frac{3}{8}\), \(\frac{8}{8}\), in a given line.

Write the fraction.
Question 8.

= ___________ = _____________
Answer: The given figure value in fractions is \(\frac{8}{8}\) = 1
Explanation: Given the square figure.
Now, we will find the number of parts and the given figure value in fractions.
The figure has 6 parts.
So, the given figure value in fractions is \(\frac{8}{8}\).
Then in these values, the value \(\frac{8}{8}\) = 1.