Students can use the Spectrum Math Grade 3 Answer Key Chapter 6 Posttest as a quick guide to resolve any of their doubts.
Spectrum Math Grade 3 Chapter 6 Posttest Answers Key
Check What You Learned
What fraction of each figure is shaded?
Question 1.
a.
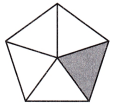
Answer: The shaded area in a fraction is \(\frac{1}{5}\).
Explanation: Given the pentagon figure,
Now, we will find the number of parts and shaded region values in fractions with numbers.
So, the pentagon has 5 parts.
The 1 part is shaded.
The shaded pentagon area in fractions is \(\frac{1}{5}\).
b.

Answer: The shaded area in a fraction is \(\frac{3}{4}\).
Explanation: Given the square figure,
Now, we will find the number of parts and shaded region values in fractions with numbers.
So, the square has 4 parts.
The 3 parts are shaded.
The shaded square area in fractions is \(\frac{3}{4}\).
c.
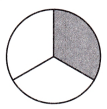
Answer: The shaded area in a fraction is \(\frac{1}{3}\).
Explanation: Given the circle figure,
Now, we will find the number of parts and shaded region values in fractions with numbers.
So, the circle has 3 parts.
The 1 part is shaded.
The shaded circle area in fractions is \(\frac{1}{3}\).
What fraction of each set is shaded?
Question 2.
a.

Answer: The shaded set area in a fraction is \(\frac{1}{4}\).
Explanation: Given the square figure set,
Now, we will write the shaded region values in fractions.
So, the shaded set value in fractions is \(\frac{1}{4}\).
b.

Answer: The shaded set area in a fraction is \(\frac{3}{5}\).
Explanation: Given the triangle figure sets,
Now, we will write the shaded region values in fractions.
So, the shaded triangle set value in fractions is \(\frac{3}{5}\).
c.
![]()
Answer: The shaded set area in a fraction is \(\frac{1}{2}\).
Explanation: Given the circle figure set,
Now, we will write the shaded region values in fractions.
So, the shaded circle set value in fractions is \(\frac{1}{2}\).
Label the fractions on each number line.
Question 3.
\(\frac{1}{4}\) and \(\frac{1}{2}\)

Answer: The given fractions on the number line is,

Explanation: Given the straight-line figure,
Now, we will place the given values.
So, after placing the values. The line is,

Question 4.
\(\frac{3}{8}\) and \(\frac{5}{8}\)

Answer: The given fractions on the number line is,

Explanation: Given the straight-line figure,
Now, we will place the given values.
So, after placing the values. The line is,

Use >, <, or = to compare the fractions.
Question 5.
a.
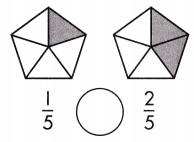
Answer: \(\frac{1}{5}\) >\(\frac{2}{5}\)
Explanation: Given the two pentagon figures with fraction values.
Now, we will find the greater fraction value in a given value.
So, the values are \(\frac{1}{5}\),\(\frac{2}{5}\).
i.e., \(\frac{1}{5}\) >\(\frac{2}{5}\).
Therefore, \(\frac{1}{5}\) is greater than \(\frac{2}{5}\).
b.
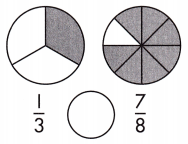
Answer: \(\frac{1}{3}\) <\(\frac{7}{8}\)
Explanation: Given the two circles figures with fraction values.
Now, we will find the lesser fraction value in a given value.
So, the values are \(\frac{1}{3}\),\(\frac{7}{8}\).
i.e., \(\frac{1}{3}\) < \(\frac{7}{8}\).
Therefore, the value \(\frac{1}{3}\) is less than \(\frac{7}{8}\).
c.
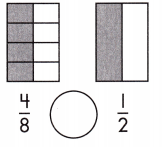
Answer: \(\frac{4}{8}\) = \(\frac{1}{2}\)
Explanation: Given the two rectangle figures with fraction values.
Now, we will find the greater, lesser, or equal fraction value in a given value.
So, the values are \(\frac{4}{8}\),\(\frac{1}{2}\).
i.e., \(\frac{4}{8}\) =\(\frac{1}{2}\).
Therefore, the value \(\frac{4}{8}\) is equal to \(\frac{1}{2}\).
What fraction of each figure is shaded? Compare the fractions. Use >, <, or =.
Question 6.
a.
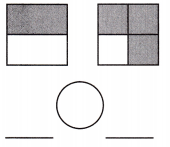
Answer: The given figure value in fractions is \(\frac{1}{2}\) \(\frac{3}{4}\)
\(\frac{1}{2}\) <\(\frac{3}{4}\).
Explanation: Given the two square figures.
Now, we will find the given figures’ values in fractions and find the greater, lesser, and equal value.
So, the given figure value in fractions is \(\frac{1}{2}\) \(\frac{3}{4}\).
Then in these values, the value \(\frac{1}{2}\) is lesser.
i.e., \(\frac{1}{2}\)<\(\frac{3}{4}\).
b.
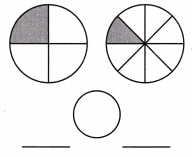
Answer: The given figure value in fractions is \(\frac{1}{4}\) \(\frac{1}{8}\)
\(\frac{1}{4}\) >\(\frac{1}{8}\).
Explanation: Given the two circle figures.
Now, we will find the given figures’ values in fractions and find the greater, lesser, and equal value.
So, the given figure value in fractions is \(\frac{1}{4}\) \(\frac{1}{8}\).
Then in these values, the value \(\frac{1}{4}\) is greater.
i.e., \(\frac{1}{4}\) >\(\frac{1}{8}\).
c.
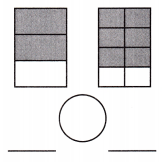
Answer: The given figure value in fractions is \(\frac{2}{3}\) \(\frac{3}{4}\).
\(\frac{2}{3}\)<\(\frac{3}{4}\).
Explanation: Given the two rectangle figures.
Now, we will find the given figures’ values in fractions and find the greater, lesser, and equal value.
So, the given figure value in fractions is \(\frac{2}{3}\) \(\frac{3}{4}\).
Then in these values, the value \(\frac{2}{3}\) is lesser.
i.e., \(\frac{2}{3}\) <\(\frac{3}{4}\).
Label the fractions on the number line.
Question 7.
\(\frac{1}{3}\) and \(\frac{3}{3}\)

Answer: The given fractions on the number line is,

Explanation: Given the straight-line figure,
Now, we will place the given values.
So, after placing the values. The line is,

Write the fraction.
Question 8.

= ____________ or _____________
Answer: \(\frac{4}{4}\) or 1.
Explanation: Given the circle figure.
Now, we will write the given figure value into fraction value.
So, the given circle figure value in fractions is \(\frac{4}{4}\) or 1.