Students can use the Spectrum Math Grade 3 Answer Key Chapter 6 Lesson 6.3 Comparing Fractions as a quick guide to resolve any of their doubts.
Spectrum Math Grade 3 Chapter 6 Lesson 6.3 Comparing Fractions Answers Key
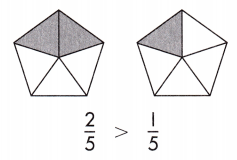
\(\frac{2}{5}\) is greater than \(\frac{1}{5}\).

\(\frac{1}{3}\) is less than \(\frac{1}{2}\).
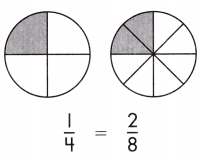
\(\frac{1}{4}\) is equal to \(\frac{2}{8}\).
Use, >, <, or = to compare the fractions.
Question 1.
a.
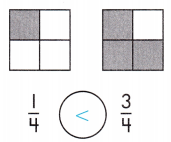
\(\frac{1}{5}\) >\(\frac{2}{5}\)
b.
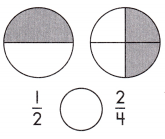
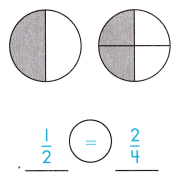
Answer: \(\frac{1}{2}\) <\(\frac{2}{4}\)
Explanation: Given the two circle figures with fraction values.
Now, we will compare the two given fraction values.
So, the values are \(\frac{1}{2}\),\(\frac{2}{4}\).
i.e., \(\frac{1}{2}\) <\(\frac{2}{4}\).
Therefore, \(\frac{1}{2}\) is less than \(\frac{2}{4}\).
c.
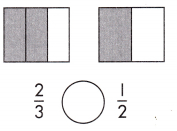
Answer: \(\frac{2}{3}\) >\(\frac{1}{2}\)
Explanation: Given the two rectangle figures with fraction values.
Now, we will compare the two given fraction values.
So, the values are \(\frac{2}{3}\),\(\frac{1}{2}\).
i.e., \(\frac{2}{3}\) >\(\frac{1}{2}\).
Therefore, \(\frac{2}{3}\) is greater than \(\frac{1}{2}\).
Question 2.
a.
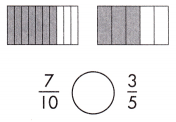
Answer: \(\frac{7}{10}\) >\(\frac{3}{5}\)
Explanation: Given the two rectangle figures with fraction values.
Now, we will compare the given two fraction values.
So, the values are \(\frac{7}{10}\),\(\frac{3}{5}\).
i.e., \(\frac{7}{10}\) >\(\frac{3}{5}\).
Therefore, \(\frac{7}{10}\) is greater than \(\frac{3}{5}\).
b.
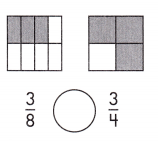
Answer: \(\frac{3}{8}\) >\(\frac{3}{4}\)
Explanation: Given the two square figures with fraction values.
Now, we will compare the two given fraction values.
So, the values are \(\frac{3}{8}\),\(\frac{3}{4}\).
i.e., \(\frac{3}{8}\) >\(\frac{3}{4}\).
Therefore, \(\frac{3}{8}\) is greater than \(\frac{3}{4}\).
c.
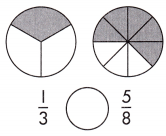
Answer: \(\frac{1}{3}\) <\(\frac{5}{8}\)
Explanation: Given the two circle figures with fraction values.
Now, we will compare the given two fractions.
So, the values are \(\frac{1}{3}\),\(\frac{5}{8}\).
i.e., \(\frac{1}{3}\) < \(\frac{5}{8}\).
Therefore, \(\frac{1}{3}\) is less than \(\frac{5}{8}\).
Question 3.
a.
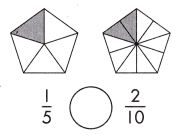
Answer: \(\frac{1}{5}\) = \(\frac{2}{10}\)
Explanation: Given the two pentagon figures with fraction values.
Now, we will compare the fraction value in a given value.
So, the values are \(\frac{1}{5}\),\(\frac{2}{10}\).
i.e., \(\frac{1}{5}\) = \(\frac{2}{10}\).
Therefore, \(\frac{1}{5}\) is equal to \(\frac{2}{10}\).
b.
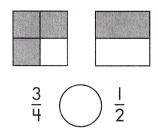
Answer: \(\frac{3}{4}\) >\(\frac{1}{2}\)
Explanation: Given the two square figures with fraction values.
Now, we will compare the given two fraction values.
So, the values are \(\frac{3}{4}\),\(\frac{1}{2}\).
i.e., \(\frac{3}{4}\) >\(\frac{1}{2}\).
Therefore, \(\frac{3}{4}\) is greater than \(\frac{1}{2}\).
c.
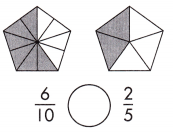
Answer: \(\frac{6}{10}\) >\(\frac{2}{5}\)
Explanation: Given the two pentagon figures with fraction values.
Now, we will compare the given two fractions.
So, the values are \(\frac{6}{10}\),\(\frac{2}{5}\).
i.e., \(\frac{6}{10}\) >\(\frac{2}{5}\).
Therefore, \(\frac{6}{10}\) is greater than \(\frac{2}{5}\).
What fraction of each figure is shaded? Compare the fractions. Use >, <, or =.
Question 1.
a.
b.
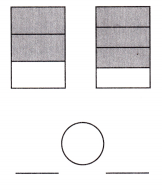
Answer: The given two rectangular figures’ fraction value is \(\frac{2}{3}\), \(\frac{3}{4}\).
\(\frac{2}{3}\) < \(\frac{3}{4}\).
Explanation: Given the two rectangle figures with fraction values.
Now, we will compare the given two fraction values.
So, the values are \(\frac{2}{3}\),\(\frac{3}{4}\).
i.e., \(\frac{2}{3}\) < \(\frac{3}{4}\).
Therefore, \(\frac{2}{3}\) is less than \(\frac{3}{4}\).
c.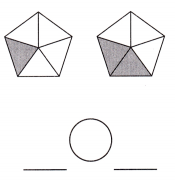
Answer: \(\frac{1}{5}\) <\(\frac{2}{5}\)
Explanation: Given the two pentagon figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{1}{5}\),\(\frac{2}{5}\).
i.e., \(\frac{1}{5}\) < \(\frac{2}{5}\).
Therefore, \(\frac{1}{5}\) is less than \(\frac{2}{5}\).
Question 2.
a.
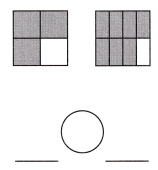
Answer: \(\frac{3}{4}\) < \(\frac{7}{8}\)
Explanation: Given the two square figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{3}{4}\),\(\frac{7}{8}\).
i.e., \(\frac{3}{4}\) < \(\frac{7}{8}\).
Therefore, \(\frac{3}{4}\) is less than \(\frac{7}{8}\).
b.
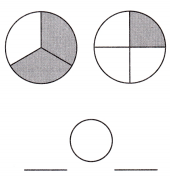
Answer: \(\frac{2}{3}\) >\(\frac{1}{4}\)
Explanation: Given the two circle figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{2}{3}\),\(\frac{1}{4}\).
i.e., \(\frac{2}{3}\) >\(\frac{1}{4}\).
Therefore, \(\frac{2}{3}\) is greater than \(\frac{1}{4}\).
c.
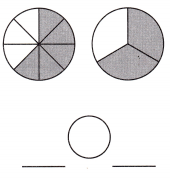
Answer: \(\frac{5}{8}\) < \(\frac{2}{3}\)
Explanation: Given the two circle figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{5}{8}\),\(\frac{2}{3}\).
i.e., \(\frac{5}{8}\) < \(\frac{2}{3}\).
Therefore, \(\frac{5}{8}\) is less than \(\frac{2}{3}\).
Question 3.
a.
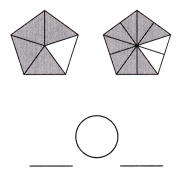
Answer: \(\frac{4}{5}\) = \(\frac{8}{10}\)
Explanation: Given the two pentagon figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{4}{5}\),\(\frac{8}{10}\).
i.e., \(\frac{4}{5}\) = \(\frac{8}{10}\).
Therefore, \(\frac{4}{5}\) is equal to \(\frac{8}{10}\).
b.
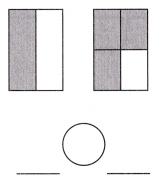
Answer: \(\frac{1}{2}\) < \(\frac{3}{4}\)
Explanation: Given the two rectangle figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{1}{2}\),\(\frac{3}{4}\).
i.e., \(\frac{1}{2}\) < \(\frac{3}{4}\).
Therefore, \(\frac{1}{2}\) is less than \(\frac{3}{4}\).
c.
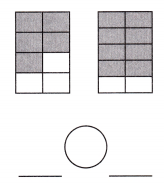
Answer: \(\frac{5}{8}\) < \(\frac{8}{10}\)
Explanation: Given the two rectangle figures with fraction values.
Now, we will compare the given fraction values.
So, the values are \(\frac{5}{8}\),\(\frac{8}{10}\).
i.e., \(\frac{5}{8}\) < \(\frac{8}{10}\).
Therefore, \(\frac{5}{8}\) is less than \(\frac{8}{10}\).