Have a look at Some Geometric Terms and Results. We have given a useful reference of geometric terms and their definitions along with solved examples. Most of the students feel difficult to understand Some Geometric Terms. So, to help such students, we explained all Geometric Terms in a clear and understandable way. We can get strong and exact results using Certain Geometric Statements. So, make use of the given formulas and get the easy process to solve problems.
We have also given Lines and Angles concepts and problems for free of cost on our website.
Some Geometric Terms and Results
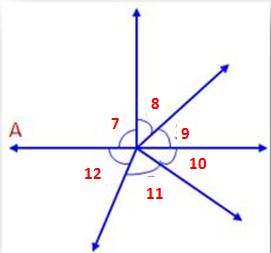
- The sum of all the angles at a point is 360°.
i.e., ∠7 + ∠8 + ∠9 + ∠10 + ∠11 + ∠12 = 360°
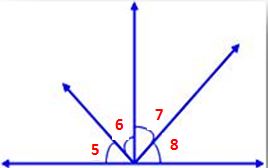
- The sum of all the angles about a point on a straight line on one side of if it is 180°.
i.e., ∠5 + ∠6 + ∠7 + ∠8 = 360°
Some Important Geometric Terms
1. Equal Angles
The two angles are considered to be equal if they have the same degree measure.
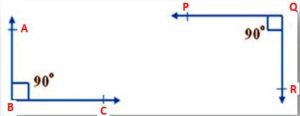
Given that two angles. The angles are ∠ABC and ∠PQR.
∠ABC = 90°; ∠PQR = 90°.
∠ABC and ∠PQR are equal angles of measure 90°.
2. Bisector of an Angle
A ray that divides the given angle into two equal angles is called an angle bisector.
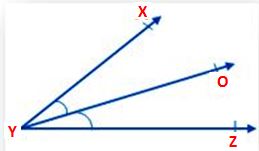
Given that ∠XYZ along with a ray YO that divides ∠XYZ. In the adjoining figure, the ray YO divides ∠XYZ into two equal angles ∠XYO and ∠OYZ
i.e., ∠XYO = ∠OYZ.
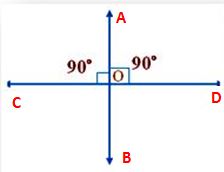
3. Perpendicular Lines
Perpendicular Lines are the lines that intersect each other to form right tangles between them. In the adjoining e, lines AB and CD intersect at 0 such that ∠COB = ∠ COA = ∠AOD = ∠BOD = 90°.
Therefore, we say that AB is perpendicular to CD, i.e., (AB ⊥ CD).
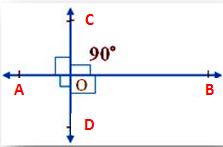
4. Perpendicular Bisector
Perpendicular Bisector is the line that passes through the midpoint of the given line segment and also it is perpendicular to it. Here, the CD is the line segment. AB is the perpendicular bisector as ∠AOB = ∠AOD = 90° and CO = OD.