Roman Numerals are a special kind of numerical notations that were used by the Romans. Different combinations of symbols are used to represent the number. Both addition and subtraction are used to convert the roman numbers to the numbers. We are 4 different rules to form a roman numeral. The rules for forming the roman numerals with examples are mentioned in the following sections of this page.
Also, Read: Roman Numerals
Roman Numeral – Definition
A Roman numeral is a numeral in a system of notation that is based on the ancient Roman system. In this system, numbers are represented by the combination of letters from the Latin alphabet. The mostly used seven symbols and their values are I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000. Addition and subtraction operations are used to find other numbers. The first 10 roman numbers are I, II, III, IV, V, VI, VII, VIII, IX, and X.
Roman Numerals Chart 1-1000
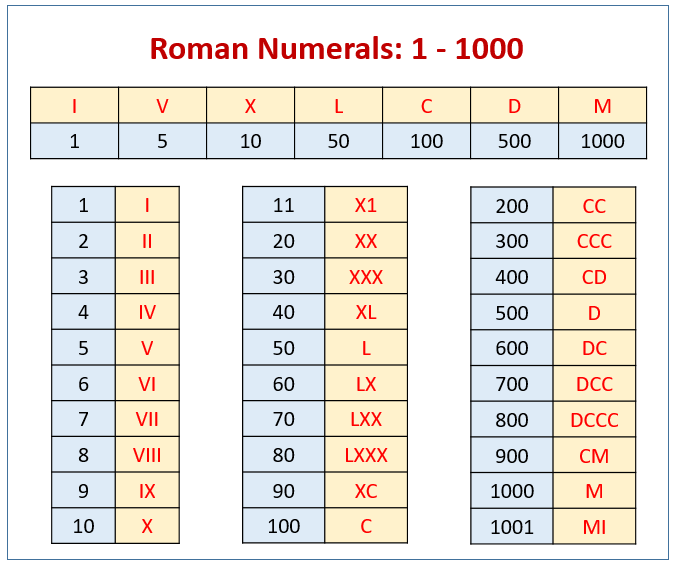
Rules for Formation of Roman Numerals
In the Roman numerals system, there is no symbol to represent the digit 0. Roman numerals system has no place value. The digit or digits of lower value is placed after or before the digit of higher value. The value of digits of lower value is added to or subtracted from the value of digits of higher value. Using these rules, you can represent a number in the numeral system.
Rule 1: Repetition of roman numeral means addition.
(i) The symbols I, X, C, and M can be repeated more than once.
The value of I is 1, X is 10, C is 50, M is 1000.
(ii) The values I, X and C can be added as
II = 1 + 1 = 2
III = 1 + 1 + 1 = 3
XX = 10 + 10 = 20
XXX = 10 + 10 + 10 = 30
CC = 100 + 100 = 200
CCC = 100 + 100 + 100 = 300
(iii) The symbols V, L, D cannot be repeated. The repetition of V, L, and D is invalid in the formation of numbers.
(iv) None of the numeral symbols can be repeated more than 3 times.
Rule 2: If a smaller numeral is written to the right side of a larger numeral, then it is always added to the larger numeral.
(i) When a digit of lower value is written to the right side or after a digit of higher value, the values of all the digits are added.
VI = 5 + 1 = 6
VII = 5 + 1 + 1 = 7
XII = 10 + 1 + 1 = 12
XV = 10 + 5 = 15
LX = 50 + 10 = 60
(ii) Value of similar digits are also added as indicated in rule 1
XXX = 10 + 10 + 10 = 30
II = 1 + 1 = 2
Rule 3: If a small numeral is written to the left side of a larger numeral, then it is always subtracted from the larger value.
(i) V, L, D can never be subtracted
(ii) I can be subtracted only from V and X.
IV = 5 – 1 = 4
IX = 10 – 1 = 9
XIV = 10 + (5 – 1) = 10 + 4 = 14
CLIX = 100 + 50 + (10 – ) = 159
XXIX = 10 + 10 + (10 – 1) = 29
However, V is never written to the left of X.
Rule 4: If a smaller numeral is located between two large numerals, then the small numeral is subtracted from the bigger numeral immediately following it.
Rule 5: When a roman number has a straight horizontal line on the top of it, then its value becomes 1000 times.
XIV = 14 but XIV = 14000
CLV = 155 but CLV = 155000
Roman Numerals Examples
Example 1:
Write the Roman numerals for the following numbers:
(i) 55
(ii) 216
(iii) 517
Solution:
(i) The given number is 55
55 = 50 + 5
= LV
So, 55 = LV
(ii) The given number is 216
216 = 100 + 100 + 10 + 5 + 1
= CCXVI
So, 216 = CCXVI
(iii) The given number is 517
517 = 500 + 10 + 5 + 1 + 1
= DXVII
So, 517 = DXVII
Example 2:
Write the numbers for the following Roman numerals:
(i) XXXVII
(ii) DXLV
(iii) XLII
Solution:
(i) The given roman numeral is XXXVII
XXXVII = 10 + 10 + 10 + 5 + 1 + 1
= 37
So, XXXVII = 37
(ii) The given roman numeral is DXLV
DXLV = 500 + (-10 + 50) + 5
= 500 + 40 + 5
= 545
So, DXLV = 545
(iii) The given roman numeral is XLII
XLII = (-10 + 50) + 1 + 1
= 40 + 1 + 1
= 42
So, XLII = 42
Example 3:
Write the Roman numerals for the following numbers:
(i) 425
(ii) 159
(iii) 61
Solution:
(i) The given number is 425
425 = (500 – 100) + 10 + 10 + 5
= CDXXV
So, 425 = CDXXV
(ii) The given number is 159
159 = 100 + 50 + (10 – 1)
= C + L + (X – I)
= CLIX
So, 159 = CLIX
(iii) The given number is 61
61 = 50 + 10 + 1
= L + X + I
= LXI
So, 61 = LXI
