Are you still looking for a simple procedure on how to represent the solution set of an inequation on a graph? If yes, then stay on this page. Here we are giving a detailed step by step explanation on finding Solution Set for Linear Inequations with the solved examples. So, refer to the following sections and solve the questions easily.
Graphical Representation of the Solution Set of an Inequation
We generally use a number line to represent the solution set of an inequation on a graph. Following are the steps to represent the solution set of a linear inequation on a graph.
- At first, solve the given linear inequation and find the solution set for it.
- Mark the solution set on a number line by putting dot.
- If the solution set is infinite, then put three more dots to indicate infiniteness.
Questions on Finding the Solution Set of an Inequation and their Representation
Example 1.
Solve the inequation 4x – 6 < 10, x ∈ N and represent the solution set graphically?
Solution:
Given linear inequation is 4x – 6 < 10
Add 6 to the both sides of inequation
= 4x – 6 + 6 < 10 + 6
= 4x < 16
Divide both sides of the inequation by 4
= 4x/4 < 16/4
= x < 4
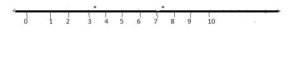
So, the replacement set = {1, 2, 3, 4, . . }
Therefore, the solution set S = {1, 2, 3} or S = {x : x ∈ N, x < 4}
Let us mark the solution set graphically.

The solution set is marked on the number line by dots.
Example 2.
Solve the inequation 8x + 4 > 20, x ∈ W and represent the solution set graphically?
Solution:
Given linear inequation is 8x + 4 > 20
Subtract 4 from both sides
= 8x + 4 – 4 > 20 – 4
= 8x > 16
Divide both sides by 8
= 8x/8 > 16/8
= x > 2
Replacement set = {0, 1, 2, 3, 4, . . . }
Therefore, solution set = {3, 4, 5, . . } or S = {x : x ∈ W, x > 2}
Let us mark the solution set graphically.
![]()
The solution set is marked on the number line by dots. We put three more dots indicate the infiniteness of the solution set.
Example 3.
Solve -2 ≥ x ≥ 5, x ∈ I, and represent the solution set graphically?
Solution:
Given linear inequation is -2 ≥ x ≥ 5
This has two inequations,
-2 ≥ x and x ≥ 5
Replacement set = {. . . -3, -2, -1, 0, 1, 2, 3 . . .}
Solution set for the inequation -2 ≥ x is -2, -1, 0, 1, 2, 3, . . i.e S = {-2, -1, 0, 1, 2, 3 . . } = P
And the solution set for the inequation x ≥ 5 is 5, 6, 7, 8 . . i.e Q = {5, 6, 7, 8 . . .}
Therefore, solution set for the given inequation = P ∩ Q
= {5, 6, 7, 8, 9 . . . }
or S = {x : x ∈ I, -2 ≥ x ≥ 5}
Let us represent the solution set graphically.
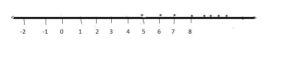
The solution set is marked on the number line by dots.
Example 4.
Solve 0 < 3x – 10 ≤ 12, x ∈ R and represent the solution set graphically.
Solution:
Given linear inequation is 0 < 3x – 10 ≤ 12
It has two cases.
Case I:
0 < 3x – 10
Add 10 to both sides
0 + 10 < 3x – 10 + 10
10 < 3x
Divide both sides by 3
10/3 < 3x/3
10/3 < x
Case II:
3x – 10 ≤ 12
Add 10 to both sides
3x – 10 + 10 ≤ 12 + 10
3x ≤ 22
Divide both sides by 3
3x/x ≤ 22/3
x ≤ 22/3
S ∩ S’ = {3.33 < x ≤ 7.33} x ∈ R
= {x : x ∈ R 3.33 < x ≤ 7.33}