Replacement Set and Solution Set are two different things. The values of the variables present in the inequality are taken from a set are known as the replacement set. Where the set of values are substitutes to make the variables true which are present in the inequalities are known as the solution set. Let us discuss deep the Replacement Set and Solution Set in Set Notation in this article. We have given different solved examples and Representation of Solution Set on Number Line, etc. in this article along with faqs. Check out the complete article to know about the Replacement Set and Solution Set.
Have a look at all the 10th grade math concepts and worksheets for the best practice. Students can gain knowledge on all the concepts in deep by referring to our website.
Also, check
- Representation of the Solution Set of a Linear Inequation
- Linear Inequality and Linear Inequations
- Practice Test on Linear Inequations
Replacement Set and Solution Set – Definition
See the Replacement Set and Solution Set Definitions below.
Replacement Set: Replacement Set is the set where the values of the variable are involved in the inequation.
Solution Set: Solution Set is the set where a number is taken from the replacement set and submitted to satisfy the given inequation. The Solution Set is the subset of the Replacement Set.
Generally, we use the set of natural numbers N (1, 2, 3, 4,….) or the set of whole numbers W (0, 1, 2, 3, 4,….) or the set of integers I (…….-3, -2, -1, 0, 1, 2, 3, …..) or the set of real numbers R is the replacement set. When we use one of these replacement sets to prove the inequality we can get the solution set.
Examples of Replacement Set and Solution Set
Let us take the inequation to be m < 5, if:
(i) The replacement set = the set of natural numbers N, then the solution set = {1, 2, 3, 4}.
(ii) If the replacement set = the set of whole numbers W, then the solution set = {0, 1, 2, 3, 4}.
(iii) If the replacement set = the set of integers Z or I, then the solution set = {……, -4, -3, -2, -1, 0, 1, 2, 3, 4}.
(iv) The replacement set = the set of real numbers R, then the solution set represents as set-builder form i.e. {m: m ∈ R and m < 5}.
Representation of Solution Set on Number Line
Take the following regulations to represent the solution of a linear inequation in one variable on the number line.
(i). If the inequation consists of ≥ or ≤, then we need to mark a point on the number line which shows the number that includes the solution set.
For example, m ≤ 3 and m ∈ R
From the given inequation m ≤ 3, 3 also included. Therefore, the graph becomes
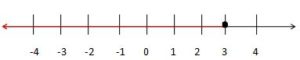
In the graph, the dark circle is darkened which represents 3 is included.
(ii) If the inequation consists of > or <, then we need to mark a point on the number line which shows the number that excludes from the solution set.
For example, m < 3 and m ∈ R
From the given inequation m < 3, 3 is excluded from the graph. Therefore, the graph becomes

In the graph, the number 3 is encircled which represents 3 is excluded.
(iii) Example for combining inequations
Solve and graph the solution set of 6x + 12 ≥ 18 and −10x > −30 where x ∈ R.
Solution: Given that 6x + 12 ≥ 18
Firstly, subtract 12 from both sides of the above equation.
6x + 12 – 12 ≥ 18 – 12
6x ≥ 6
Now, divide the above equation with 6 into both sides.
x ≥ 1.
![]()
−10x > −30
Now, divide the above equation with -10 into both sides. As we know that the inequality reverses on multiplying pr dividing both sides by -1.
−10x/-10 > −30/-10
x < 3
![]()
Therefore, the graph of the solution set of x ≥ 1 and x < 3. Take the common points from both x ≥ 1 and x < 3 and draw the graph.
![]()
Examples on Solving Equations by Plugging in Values
Check out all the examples given below and follow the step-by-step procedure to learn the complete procedure of solving problems.
Question 1. If the replacement set is the set of integers (I or Z), between −6 and 8, find the solution set of 30 − 6x > 2x − 6.
Solution: Given that 30 − 6x > 2x − 6
Now, move the 2x on the left side of the above equation.
30 – 6x – 2x > -6
30 – 8x > -6
Now, subtract 30 from both sides of the above equation.
30 – 30 – 8x > -6 -30
-8x > -36
Now, divide the above equation with -8 into both sides. The inequality reverses on multiplying pr dividing both sides by -1.
x < 4.5
Given that the replacement set is the set of integers between −6 and 8. Therefore, solution set ={–5, –4, –3, –2, –1, 0, 1, 2, 3, 4}
Question 2. If the replacement set is the set of real numbers (R), find the solution set of 10 − 6x < 22.
Solution: Given that 10 − 6x < 22.
Now, subtract 10 from both sides of the above equation.
10 – 10 − 6x < 22 – 10
– 6x < 12
Now, divide the above equation with -6 into both sides. The inequality reverses on multiplying pr dividing both sides by -1.
-6x/-6 < 12/-6
x > -2
Given that the replacement set is the set of real numbers R. Therefore, solution set ={x : x > – 2 and x ∈ R}.
Question 3.
List the solution set of 100 – 6(2x–5) < 50, given that x ∈ W. Also, represent the solution set obtained on a number line.
Solution:
Given that 100 – 6(2x–5) < 50.
100 – 12x + 30 < 50.
130 – 12x < 50
Now, subtract 130 from both sides of the above equation.
130 -130 – 12x < 50 – 130
-12x < – 80
Now, divide the above equation with -12 into both sides. The inequality reverses on multiplying pr dividing both sides by -1.
-12x/-12 < – 80/-12
x > 6.66
Therefore, the solution set is {7, 8, 9,…..}. The number line is
![]()
Question 4.
Solve the inequation 74 – (6x + 10) ≥ 18x – 16(x–3) represent the solution set on the number line. x is a whole number.
Solution:
Given that 74 – (6x + 10) ≥ 18x – 16(x–3)
74 – 6x – 10 ≥ 18x – 16x + 48
64 – 6x ≥ 2x + 48
Move 6x on the right side of the above equation.
64 ≥ 2x + 6x + 48
64 ≥ 8x + 48
Now, subtract 48 from both sides of the above equation.
64 – 48 ≥ 8x + 48 – 48
16 ≥ 8x
Now, divide the above equation with 8 into both sides.
16/8 ≥ 8x/8
2 ≥ x.
x ≤ 2
Therefore, the solution set becomes (−∞, 2). On the number line, we can represent it as
![]()
Question 5.
Write the solution of the following inequation in the set notation form 10x − 20 ≤ 4x + 4.
Solution:
Given that 10x − 20 ≤ 4x + 4.
Move 4x on the left side of the above equation.
10x – 4x – 20 ≤ 4
6x – 20 ≤ 4
Now, add 20 on both sides of the above equation.
6x – 20 + 20 ≤ 4 + 20
6x ≤ 24
Now, divide the above equation with 8 into both sides.
6x/6 ≤ 24/6
x ≤ 4.
Therefore, the solution set is {x : x ≤ 4, x ∈ R} or (−∞, 4)
FAQs on Replacement Set and Solution Set in Set Notation
1. What are the replacement set and solution set?
The values of variables are taken from the replacement set. The number taken from the replacement set makes the inequation true by substituting it in the inequation.
2. How do you write a solution set?
The solution set represents the collection of all the solutions to that equation. If we don’t get any solution, then we can represent it with Φ. We call it a null set or empty set.
3. What is the solution set in linear inequalities?
The solution set of the inequality means the number or value that makes the given inequation true when that number or value is substituted in the variable of an inequation.
Example: Let us take m > 6 where Replacement set = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Therefore, the Solution set is {7, 8, 9, 10}.
4. What is the replacement set in linear inequalities?
The Replacement set in linear inequalities is the representation of the values of variables that belong to and involves in the inequation.
Example: Let us take m < 2 where the Replacement set = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Therefore, the Solution set is {1}.
5. What is linear inequality?
Linear Inequalities are the inequalities when two mathematical expressions or two integers are compared they will not become equal. A linear inequation in one variable can always be written as ax + b < 0, ax + b > 0, x + b ≤ 0, or ax + b ≥ 0 where a and b are real numbers, a≠0.
