Do you want to know all about the Recurring Decimals? If so, you have come the right way where you will find complete details regarding the Repeating Decimals such as definition, procedure on how to convert fractions to repeating decimals, etc. Also, check out Solved Examples on Repeating Decimals for better understanding of the concept.
Also, Read:
Recurring Decimal – Definition
Recurring Decimal or Repeating Decimal is a Decimal in which a digit or sequence of digits repeats itself infinitely.
For Example, 1/3 can be written in decimal form as 0.3333…….. where the digit repeats 3 infinitely.
The part that repeats can also be denoted by placing a bar on the digit or the digit that repeats itself. In fact, you can also place a dot on the first and last digits of the repeating pattern. We can denote the recurring decimal 0.3333…….. as 0.\(\overline{3}\)
Conversion of Fractions to Recurring Decimals | How to turn a Fraction to Repeating Decimal?
Follow the simple and easy steps listed for converting a fraction to a repeating decimal. They are along the lines
- The first and foremost step to keep in mind while converting a fraction to a repeating decimal is simply to divide the numerator with a denominator.
- At times whenever we perform division the digits clearly repeat and in such cases, we write the result as a repeating decimal.
If you want to clearly understand the concept of converting fractions to repeating decimals check out few worked-out examples provided in the below modules.
Solved Examples on Recurring Decimals
1. Convert the Fraction \(\frac { 4 }{ 9 } \) to Decimal Form and Check if it is a Recurring Decimal or not?
Solution:
Firstly divide the numerator 4 with 9 and after performing the division and the digit 4 keeps repeating infinitely. The result is a repeating decimal. So to express the fraction \(\frac { 4 }{ 9 } \) in the form of a recurring decimal by simply placing a bar on the repeating digit itself.

\(\frac { 4 }{ 9 } \) = 0.44444444…….. (or)0.\(\overline{4}\)
Thus \(\frac { 4 }{ 9 } \) expressed as repeating decimal is 0.\(\overline{4}\)
2. Convert the Fraction \(\frac { 2 }{ 3 } \) to Decimal Form and Check if it is a Recurring Decimal or not?
Solution:
Firstly divide the numerator 2 with 3 and after performing the division we will see the digit 6 keeps repeating infinitely. The result is a repeating decimal. So to express the fraction \(\frac { 2 }{ 3 } \) in the form of a recurring decimal by simply placing a bar on the repeating digit itself.
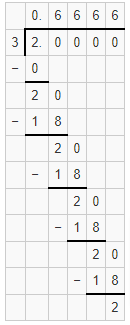
\(\frac { 2 }{ 3 } \) = 0.6666666…….. (or)0.\(\overline{6}\)
Thus \(\frac { 2 }{ 3 } \) expressed as repeating decimal is 0.\(\overline{6}\)
3. Express \(\frac { 13 }{ 45 } \) to Decimal Form and Check if it is a Recurring Decimal or not?
Solution:
Firstly divide the numerator 13 with 45 and after performing the division we will see the digit 8 keeps repeating infinitely. The result is a repeating decimal. So to express the fraction \(\frac { 13 }{ 45 } \) in the form of a recurring decimal by simply placing a bar on the repeating digit itself.
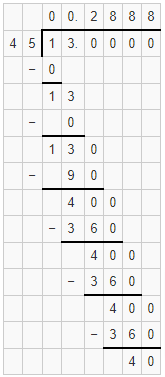
\(\frac { 2 }{ 3 } \) = 0.28888888…….. (or)0.2\(\overline{8}\)
FAQs on Repeating Decimals
1. What is a Repeating Decimal?
A Recurring Decimal is a decimal in which a digit or sequence of digits repeats itself infinitely.
2. How do you determine the repeating decimals?
Just divide the numerator with the denominator and if you end up with remainders repeating after some point then it is a repeating decimal.
3. Is \(\frac { 1 }{ 3 } \) a recurring decimal?
Yes, \(\frac { 1 }{ 3 } \) is a recurring decimal as it is equivalent to 0.333333….. and the digit 3 repeats infinitely.
