The Ratio in Simplest Form Article will assist students in learning the questions on how to write a given ratio in the simplest or lowest form. Ratios in Lowest Form Examples are available for 6th Grade Math Students so that they can practice at their own pace and gradually move on to difficult level problems on the topic too.
Rely on the visual simulations in the interactive Ratios in Simplest Form exercises and have a better understanding of the topic. On this page, Students will learn about the definition of ratio, how to reduce the ratios in simplest form, some solved example problems on reducing ratios to lowest forms, etc all explained step by step.
Read More:
Definition of Ratio
In some cases, the comparison of two quantities by the method of division is really efficient. In Simple Terms, we can say that the comparison or simplified form of two quantities of the same kind is referred to as a ratio. This relation explains to us how many times one quantity is equal to the other quantity. In simple words, the ratio is the number that can be used to express one quantity as a fraction of the other ones.
The two numbers in a ratio will only be compared when they have the same unit. For comparing two things we will use ratios. The ratio sign is denoted as ‘:’. The ratio can be represented in three different forms, such as:
- a to b
- a:b
- a/b
How do you Write a Ratio in Simplest Form?
We will learn how to express the ratios in the simplest form here. They are as follows
- A ratio between two quantities of the same kind and in the same units is attained by dividing one quantity by the other and having no unit. A ratio will be independent of the units used in the quantities to compare.
- The ratio will always be expressed in its simplest form or in its smallest terms. A ratio will be in the simplest form or in the smallest term if the ratio of two quantities that is antecedent and consequent are no common factor (means antecedent and consequent are co-primes) other than 1 (or their HCF value is 1.)
Simplifying Ratios to Lowest Form Examples | Ratio in Simplest Form Examples
Example 1:
Write each of the following ratios in the simplest form
(i) 10: 30
(ii) 2/7: 3/7
(iii) 9: 18
(iv) 5 : 1 1/2
(v) 24 : 36
(vi) 22 : 55
(vii) 42 : 56
(viii) 250 : 300
Solution:
Given that
(i) 10:50
When we divide by 10 we get,
10/10:30/10
The ratio is 1:3.
Therefore, the simplest form of the 10:30 ratio is 1:3.
(ii) 2/7:3/7
When we divide by 7 we get,
2/7:3/7 = 2:3
Hence, the simplest form of 2/7:3/7 is 2:3.
(iii) 9:18
When we divide by 9 we get,
9/9:18/9
1:2
Hence, the simplest form of the 9:18 ratio is 1:2.
(iv) 6: 1 1/2
Now, convert the second part is 1 1/2 as an improper fraction, we get
= 6 : 3/2
Now, multiplying both parts by 2, we get
= 6(2) : (3/2)(2)
= 12 : 3
Next, Dividing by 3, we get
= 4 : 1
So, the simplest form is 4: 1.
(v) 24:36
When we divide by 6 we get,
24/6:36/6
4:6
When we divide by 2 we get,
=2:3
Thus, the simplest form of 24:36 is 2:3.
(vi) 22:55
When we divide by 11 we get,
22/11:55/11 = 2:5.
So, the ratio in the simplest form of 22:55 is 2:5.
(vii) 42:56
When we divide by 7 we get,
42/7:56/7
6:8
When we divide by 2 we get,
3:4
Therefore, the ratio of 42:56 in simplest form is 3:4.
Example 2:
Express the following ratios in the same units and then express them in their lowest term.
(i) 2 kg : 600 gm
(ii) 5 cm : 3 m
(iii) 2 m : 60 cm
(iv) 1 year : 8 months
(v) 2 hour : 40 minutes
(vi) 3 minutes : 50 seconds
(vii) 50 kg : 1 quintal
(viii) 50 paise : 1 Rupee
(ix) 300 m : 6 km
(x) 4 hours : 1 day
Solution:
(i) 2 kg : 600 gm
we know that 1 kg=1000 gm.
2000 gm: 600 gm
20:6
By dividing with 2 we get
20/2:6/2
10:3
The simplest form is 10:3.
(ii) 5cm:3m
We know that 1m=100 cm.
5cm:300 cm
1:60
(iii) 2 m : 60 cm
we know that 1m=100 cm.
200 cm:60 cm
20 cm:6 cm
Divide with 2, we get
20/2 cm:6/2 cm
10 :3
(iv) 3 minutes : 50 seconds
we know that 1 minute=60 second.
180 seconds: 50 seconds
18:5
(v) 2 hour : 40 minutes
we know that 1 hour=60 minute.
120 minutes:40 minutes
By dividing with 4 we get,
3:1
(vi) 3 minutes : 50 seconds
we know that 1 minute=60 second.
180 seconds:50 seconds
18:5
(vii) 50 kg: 1 quintal
we know that 1 quintal=1000 kg
50 kg:1000 kg
divide with 50 we get,
1:20
(viii) 50 paise : 1 Rupee
we all know that 1 rupee=100 paise.
So, 50 paise:100 paise
Divide with 50, we get
Hence the ratio is 1 paise:2 paise.
(ix) 300 m: 6 km
we know that 1 km=1000 m.
300 m: 6000 m
3:60
By dividing with 3 we get,
3/3:60/3
Thus, the simplest form ratio is 1:20.
(x) 4 hours : 1 day
we know that 1 day=24 hour.
4 hours: 24 hours
By dividing with 4, we get
The final ratio is 1:6.
Example 3:
Express as a ratio in simplest form
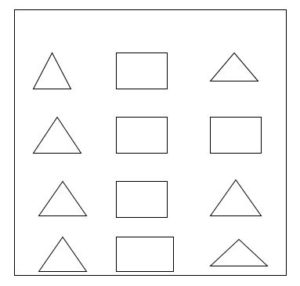
a) Find the ratio of the number of triangles to squares
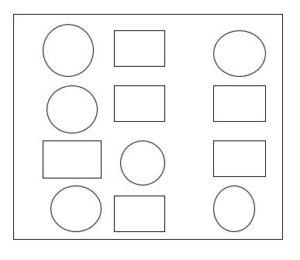
b) Find the ratio of the number of circles to squares
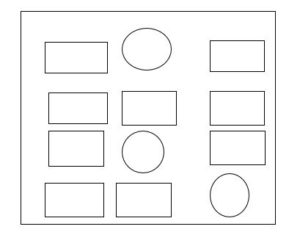
c) Find the ratio of the number of rectangles to circles
Solution:
As given in the question,
a) In the given diagram,
No. of triangles are 7
No. of squares are 5
The ratio of no. of triangles to squares is 7/5
Therefore, the ratio of triangles to squares is 7/5.
b) In the given diagram,
No. of circles are 6
No. of squares are 6
The ratio of no. of circles to squares is 6/6=1:1.
Thus, the ratio of no. of circles to squares will be 1:1.
c) In the given figure,
No. of rectangles is 9
No. of circles are 3
The ratio of no. of rectangles to squares is=9/3=3:1.
Therefore, the no. of rectangles to squares ratio is 3:1.
Example 4:
Write each of the following ratios in the form of 1: n
a) 2: 5
b) 3: 8
c) 6: 12
d) 12: 7
e) 9: 19
f) 6: 49
Solution:
Given that,
a) 2:5
By dividing with 2, we get
2/2:5/2
Then, the ratio is 1:2.5
b) 3: 8
By dividing with 3, we get
3/3:8/3
So, the ratio is 1: 2.6
c) 6:12
By dividing with 6, we get
6/6:12/6
Therefore, the ratio in simplest form is 1:2
d) 12: 7
By dividing with 12, we get
12/12:7/12
So, the ratio is 1:0.5
e) 9:19
By dividing with 9, we get
9/9:19/9
Thus, the ratio in simplest form is 1:2.1
f)6:49
By dividing with 6, we get
6/6:49/6
The ratio is 1:8.1
Example 5:
Find each of the following ratios in the form of n: 1.
a) 9: 4
b) 7: 5
c) 14: 6
d) 3: 7
e) 5: 10
(f) 18: 9
Solution:
As given in the question,
a) 9:4
By dividing with 4, we get
9/4:4/4
So, the ratio is 2.2:1.
b) 7:5
By dividing with 5, we get
7/5:5/5
Thus, the ratio is 1.4:1.
c) 14: 6
By dividing with 6, we get
14/6:6/6
Therefore, the ratio is 2.3:1.
d) 3: 7
By dividing with 7, we get
3/7:7/7
So, the ratio in simplest form is 0.4:1.
e) 5: 10
By dividing with 10, we get
5/10:10/10
Hence, the final simplest ratio is 0.5:1.
(f) 18: 9
By dividing with 9, we get
18/9:9/9
Thus, the final ratio is 2:1.
Example 6:
In a Gym, there are 6 adults and 15 children. What is the ratio of adults to children?
Solution:
Given that,
No. of adults in the gym is 6.
No. of the children in the gym is 15.
Now, we will find the ratios of given data
So, the ratio of adults to children in simplest form is =6/15=2/5
Therefore, the ratio of adults to children in the gym is 2/5.
Example 7:
Sam mixes 2 liters of red color with 1 liter of water. Find the ratio of water to red color?
Solution:
As given in the question,
No. of liters of red color is 2.
No. of liters of water is 1.
Now, we have to find the ratio in the simplest form.
So, the ratio of water to red color is=1/2.
Hence, the total ratio of water to red color is 1/2.
Example 8: In a Function hall, there are 550 men and 450 women. Find the ratio of men and women in the auditorium?
Solution:
Given that,
No. of men in the auditorium=550
No. of women in the auditorium=450
Now, we will find the ratio in the simplest form.
The ratio of men and women in the auditorium is = 550/450 = 11/9
Therefore, the ratio of men and women in the auditorium is 11:9.