The basic four different arithmetic operations are addition, subtraction, multiplication, and division. To perform these arithmetic operations, you just need at least two whole numbers. Subtraction means removing objects from a group. It is represented using the minus sign “-“.
The other names of subtraction are minus, difference, deduct, less, decrease, and take away. For subtracting larger whole numbers, you can use subtraction with regrouping (borrowing) or quick subtraction or subtraction or addition methods. Interested students can read further sections to know five different properties of subtraction of whole numbers along with solved examples.
Also Check:
Subtraction Properties List

How to Subtract Two Whole Numbers?
Students can subtract two larger whole numbers by following these steps.
- Let us take two numbers one is minuend, second is subtrahend.
- Write the number that is to be subtracted from on the top and the number that is to be subtracted on the bottom.
- Begin the process from the rightmost digits of the numbers.
- If the minuend digit is lesser than the subtrahend digit, then barrow 10 from the next digit of minuend which is on the left side.
- Add 10 to the minuend digit and subtract the result from the subtrahend’s digit.
- Don’t forget to mention the borrowed value on the top of the digit.
- Then the next digit becomes (digit – 1)
- Repeat the steps till you are left with nothing on the left side.
Closure Property of Subtraction of Whole Numbers
When a whole is subtracted from another whole number, the difference is not always a whole number. It says that whole numbers not closed under subtraction.
If a, b are two whole number and their difference a – b = c, then c is not always a whole number.
Verification:
To verify the closure property of subtraction, let us take few pairs of whole numbers and subtract them and check whether the difference is a whole number or not.
Examples:
15 – 5 = 10 (whole number)
259 – 8 = 251 (whole number)
45 – 48 = -3 (Not whole number)
16 – 0 = 16 (whole number)
Subtractive Property of Zero
If a whole number is subtracted from zero, then the result will be the same whole number. But when zero is subtracted from a whole number, the result is undefined.
If a is a whole number, then a – 0 = a but 0 – a is undefined.
Verification:
Let us take some whole numbers and subtract zero from them and check whether the difference is given the whole number or not. Again subtract 0 from the whole number and check the difference.
Examples:
15 – 0 = 15 but 0 – 15 is not possible
2 – 0 = 2 but 0 – 2 is undefined
84 – 0 = 84 but 0 – 84 is not defined
Commutative Property of Subtraction of Whole Numbers
The commutative property of subtraction says that the swapping of terms will affect the difference value. So, the subtraction of two whole numbers is not commutative.
If a and b are two whole numbers, then (a – b) is never equal to (b – a).
Verification:
Let us consider two whole numbers and subtract one from the other by interchanging their places and check whether their differences are equal or not as shown below:
Examples:
15 – 4 = 11 and 4 – 15 = -11
So, 15 – 4 ≠ 4 – 15
82 – 45 = 37 and 45 – 82 = -37
So, 82 – 45 ≠ 45 – 82
6 – 10 = -4 and 10 – 6 = 4
So, 6 – 10 ≠ 10 – 6
Associative Property of Subtraction of Whole Numbers
The associative property is not there for the subtraction of whole numbers. We can’t group any two whole numbers and subtract them first. Order of subtraction plays an important role.
If a, b, c are three whole numbers, then a – (b – c) is not equal to (a – b) – c.
Verification:
Assume three whole numbers, find the difference between any two and again subtract the result from the third one. Now, interchange the numbers and find the difference to check whether both differences are equal or not.
Examples:
1. 15 – (10 – 2) = 15 – 8 = 7
(15 – 10) – 2 = 5 – 2 = 3
Therefore, 15 – (10 – 2) ≠ (15 – 10) – 2
2. 28 – (6 – 4) = 28 – 2 = 26
(28 – 6) – 4 = 22 – 4 = 18
Therefore, 28 – (6 – 4) ≠ (28 – 6) – 4
3. (156 – 120) – 10 = 36 – 10 = 26
156 – (120 – 10) = 156 – 110 = 46
Therefore, (156 – 120) – 10 ≠ 156 – (120 – 10)
Property 6
If a, b, c are the whole numbers and a – b = c, then a = c + b.
Verification:
Let us take any three whole numbers, subtract the second whole number from the first, the difference should be a third whole number or the first number is equal to the sum of the second and third numbers.
Examples:
18 – 0 = 18 and 18 = 18 + 0
So, whenever zero is subtracted from any whole number, then we get the whole number.
18 – 18 = 0
So whenever a number is subtracted from the same number, then the difference is zero.
1850 – 1 = 1849 and 1849 + 1 = 1850.
Solved Examples on Properties of Subtraction of Whole Numbers
Example 1:
Solve the following.
(i) 415 – 0
(ii) 710 – 2
(iii) 5645 – 455
Solution:
(i) The given whole numbers are 415, 0
As per the identity property, if any number is subtracted from 0, then the difference is a whole number.
So, 415 – 0 = 415.
(ii) The given whole numbers are 710, 2
710 – 2 = 708.
(iii)
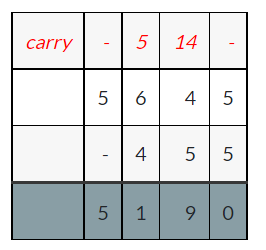
5645 – 455 = 5190.
Example 2:
Find the missed numbers from the following.
(i) 258 – _____ = 0
(ii) ______ – 90 = 88
(iii) 1652 – ______ = 10
Solution:
(i) 258 – x = 0
We already know that a – b = c, then a = c + b.
258 – 0 = x
As per the identity property, if any number is subtracted from 0, then the difference is a whole number.
So, 258 – 0 = 0
(ii) x – 90 = 88
We already know that a – b = c, then a = c + b.
x = 88 + 90
x = 178
So, 178 – 90 = 88.
(iii) 1652 – x = 10
We already know that a – b = c, then a = c + b.
1652 – 10 = x
x = 1642
So, 1652 – 1642 = 10.
Example 3:
State whether the following statements are correct or not.
(i) 56 x (85 – 25) = 56 x 85 – 56 x 25
(ii) 182 – (72 – 38) = (182 – 72) – 38
(iii) 546 – 546 = 1
Solution:
(i) The given statement is 56 x (85 – 25) = 56 x 85 – 56 x 25
L.H.S = 56 x (85 – 25)
= 56 x 60
= 3360
R.H.S = 56 x 85 – 56 x 25
= 4760 – 1400
= 3360
So, L.H.S = R.H.S
Therefore, the stament is true.
(ii) The given statement is 182 – (72 – 38) = (182 – 72) – 38
L.H.S = 182 – (72 – 38)
= 182 – 34
= 148
R.H.S = (182 – 72) – 38
= (110) – 38
= 72
L.H.S ≠ R.H.S
Therefore, the statement is false.
(iii) The given statement is 546 – 546 = 1
We know that, if a number is subtracted from the same whole number, then the result is zero.
Therefore, the statement is false.
FAQs on Properties of Subtraction
1. Write the different properties of subtraction?
The five various subtraction properties are closure property, subtractive property of zero, commutative property, and associative property.
2. Describe the terms minuend, subtrahend, and difference?
A minuend is a number that is to be subtracted from, a subtrahend is a number that is to be subtracted, and the difference is the result of subtracting one number from another number.
3. What is the difference between distributive property and associative property.
Distributive property for subtraction is true but associative property for subtraction is false. Distributive property is a x b – a x c = a x (b – c). Associative property is a – (b – c) ≠ (a – b) – c.
