The Least Common Multiple is the smallest number of all common multiples. Students can find the L.C.M of the numbers by finding the common prime factors, division method, listing multiples, prime factorization, etc. Go through the below section to know the properties of L.C.M or Least Common Multiples and solve the problems easily. Practice the given problems and score the highest marks in the exams.
Do Check:
Least Common Multiple Definition
LCM stands for Least Common Multiple is the smallest positive number that will be divisible by each of them. LCM is used before fractions can be added, subtracted, or compared.
Properties of LCM
The properties of the Least Common Multiples are discussed below,
- The L.C.M. of two or more numbers cannot be less than any one of them.
- In a given set of two natural numbers if one number is the factor of the other number, then the LCM will be the bigger number.
- L.C.M is Associative that means, LCM(a,b)= LCM(b,a)
- L.C.M is Communicative, that means LCM (a, b, c) = LCM (LCM (a, b), c) = LCM (a, LCM(b, c))
- The LCM of 2 prime numbers will be the product of the two given numbers.
Example: What is the LCM of 3 and 5.
The LCM of 3 and 5 is 15.
LCM Examples
Example 1.
Find the LCM of two numbers 6 and 12.
Solution:
The LCM can be found by multiplying the highest exponent prime factors of 6 and 12.
First we will calculate the prime factors of 6 and 12.
Prime Factorization of 6
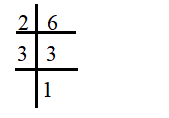
Prime factors of 6 are 2, 3
Prime Factorization of 12
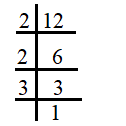
Prime factors of 12 are 2, 3.
Now multiplying the highest prime factors to calculate the LCM of 6 and 12.
Factors of 6
6 = {1, 2, 3, 6}
Factors of 12
12 = {1, 2, 3, 4, 6, 12}
Example 2.
Find the LCM of 8 and 24.
Solution:
The LCM can be found by multiplying the highest exponent prime factors of 8 and 24.
First we will calculate the prime factors of 8 and 24.
Prime Factorization of 8
Prime factors of 8 are 2.
The prime factorization of 8 is 2 × 2 × 2.
Prime Factorization of 24
The prime factors of 24 are 2, 3.
24 = 2 × 2 × 2 × 3
LCM(8, 24) = 24
Factors of 8
List of positive integer factors of 8 that divides 8 without a remainder.
8 = 1, 2, 4, 8
Factors of 24
List of positive integer factors of 24 that divides 24 without a remainder.
24 = 1, 2, 3, 4, 6, 8, 12, 24
Example 3.
How to find the LCM of 7 and 21?
Solution:
LCM of 7 and 21 = 21
Step 1: Find the prime factorization of 7
7 = 7
Step 2: Find the prime factorization of 21
21 = 3 × 7
Step 3: Multiply each factor the greater number of times it occurs in steps i and ii
LCM = 21 = 3 × 7
Step 4: Therefore the Least Common Multiple of 7 and 21 is 21.
Example 4.
Find the LCM of 12 and 96.
Solution:
The Least Common Multiple of 12 and 96 = 96
Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 96 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96.
Step 1: Find the prime factorization of 12
12 = 2 × 2 × 3
Step 2: Find the prime factorization of 96
96 = 2 × 2 × 2 × 2 × 2 × 3
Step 3: Therefore the Least Common Multiple of 12 and 96 is 96.
Example 5.
Find the factors of 625 and 5.
Solution:
The Least Common Multiple of 625 and 5 = 625
The factors of 5 are 1, 5. There are two integers that are factors of 5. The greatest factor of 5 is 5.
The factors of 625 are 1, 5, 25, 125, 625. There are 5 integers that are factors of 625. The greatest factor of 625 is 625.
Step 1: Find the prime factorization of 625
625 = 5 × 5 × 5 × 5
Step 2: Find the prime factorization of 5
5 = 5
Step 3: Multiply each factor the greater number of times it occurs in step i and step ii.
LCM = 625 = 5 × 5 × 5 × 5
FAQs on Properties of L.C.M
1. What is the rule of LCM?
The LCM of two or more numbers is equal to the product of each factor by the maximum number of times it appears in the prime factorization of those numbers.
2. Write any 2 Properties of L.C.M.
1. LCM is Associative that means, LCM(a,b)= LCM(b,a)
2. The LCM of 2 or more numbers can not be less than the smallest numbers given in the set.
3. Why do we use Least Common Multiples(LCM)?
The L.C.M or L.C.D can be used before fractions can be added, subtracted, or compared. The LCM is the smallest positive number that is divisible by each of them.
