A factor is one of two or more numbers that divides a given number without a remainder. Here we learn the different properties of factors to solve the problems. Know how to find the factors of different numbers from here. There are two methods to find the factors of the numbers. They are the division method and factor tree method. Scroll down this page to know different methods to find the factors with the help of properties of factors.
Also, Refer:
Factor – Definition
Factors are defined as the numbers that are multiplied to give the product. For Example, Factors of 18 are 1, 2 3, 6, 9, 18. All these divide the number 18 exactly.
Chart of Properties of Factors
Here is the Factors Properties Chart the lists the major properties. You can employ them while solving related problems and arrive at solutions easily.

Properties of Factors
Follow the properties given below to know how to find the factors of the multiples.
Property 1.
1 is a factor of every number.
Example:
Multiply 1 with any number you get the same number.
1 × 31 = 31
1 × 534 = 534
1 × 76 = 76
1 × 467 = 467
Property 2.
Every number is a factor of itself.
Example: Multiply any number with 1 you get the original number.
15 × 1 = 15
5464 × 1 = 5464
530 × 1 = 530
66468 × 1 = 66468
Property 3.
Every factor of a number is an exact divisor of that number.
Example:
Factors of 10 are 1, 2, 5, 10.
Here each factor is exactly divisible by 10.
Property 4.
Every factor of a number is less than or equal to the number.
Example:
6 = 2 × 3
Here 2 and 3 are the factors that are less than 6.
Property 5.
Factors of a given number are finite.
Property 6.
Every multiple of a number is greater than or equal to that number.
Example:
Multiple of 2 = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
Property 7.
Every number is multiple in itself.
Property 8.
The number of multiples of a given number is infinite.
Examples on Finding the Factors using Properties
Example 1.
Find the factors of 8 using the factor tree method.
Solution:
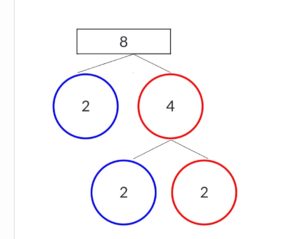
Factor tree of 8 is the list of prime numbers when multiplied results in the original number.
If we write into multiples it would be 4 × 2.
On splitting 4 further and writing it as multiples of number it would be 2 × 2.
Altogether expressing the number in terms of prime factors would be 2 × 2 × 2.
Example 2.
Find the factors of 72 using the factor tree method.
Solution:
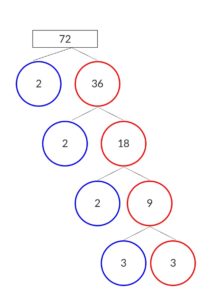
72 = 2 × 36
9 = 3 × 3
Split 72 into two pairs 2 × 36
Now split 36 we get 36 = 2 × 18
Now split the factors of 18 into two 18 = 2 × 9.
On splitting 9 we get 3 × 3.
Altogether expressing the number in terms of prime factors 2 × 2 × 2 × 3 × 3.
Example 3.
What are the factors of 18?
Solution:
The factors of 18 are as follows
1 × 18
2 × 9
3 × 6
6 × 3
9 × 2
18 × 1
Thus the factors of 18 are 1, 2, 3, 6, 9, and 18.
Example 4.
What are the prime factors of 25?
Solution:
Prime factors of a number are the set of prime numbers which when multiplied by together give the actual number.
We have to multiply directly with the prime number to find the factors of 25.
25 = 5 × 5
Thus the prime factors of 25 are 5.
Example 5.
What are the factors of 30?
Solution:
The factors of 30 are as follows
30 = 1 × 30
30 = 2 × 15
30 = 3 × 10
30 = 5 × 6
30 = 6 × 5
30 = 10 × 3
30 = 15 × 2
30 = 30 × 1
Thus the factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
FAQs on Properties of Factors
1. What are the properties of factors?
1. Smallest Multiple is the Number itself.
2. There can be an infinite number of multiples.
3. Multiples are greater than or equal to the given number.
2. What is a factor?
A factor is a number or an algebraic expression that divides another number or expression evenly with no remainder.
3. How many types of factors are there?
Factors are classified into two types.
1. Prime factors
2. Composite factors
