Prime Factors are simply factors of number which are Prime Numbers. The ‘Prime Factors’ are composed of two distinct words one is prime and another word is factors and they are very important in mathematics. The number that may be multiplied together to induce another number could be a factor. Suppose when the division of a number with all the factors results in 0 remainders, that factor is an exact divisor of that number.
In this article, you will learn about Prime Factors, finding prime factors of a number using the division method, some examples explaining how to find the prime factor, how to find the prime factorization of a number using the Factor Tree method, and so on.
Also, Read:
Prime Factors – Definition
Prime Factors means a group of prime numbers that are multiplied together to get the actual number. In other words, Prime factors are factors of a number that are, themselves, prime numbers. We have many methods for finding prime factors, but the most commonly used method is finding prime factors using the factor tree method.
Consider a value is 6, the prime factor of value 6 is 3 x 2. So, the prime factors of 6 are 3 and 2. Now, take another value 8, the prime factors of value 8 are, 4×2 and 2x2x2. Here will take only 2 as a prime factor as 4 is not a prime number.
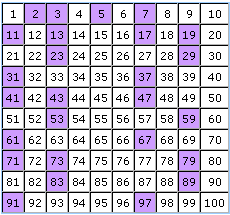
The Prime Factors Table for 1-100 Numbers is as shown below,
How to find Prime Factors of a Number through Division Method?
Following are the steps for finding the prime factor of any given number. Remember and follow these steps
Step 1: First, by dividing the given number by the first prime number 2.
Step 2: Continue dividing by 2 until you get a decimal or remainder. Then divide the next prime numbers like 3, 5, 7, etc. Until the numbers left are prime numbers.
Step 3: Now, write the number as a product of prime numbers.
The method of finding prime factors of any given number is called Prime Factorization. Prime Factorization means any number written in the form of multiplication of their prime factors and the original number is evenly divisible by these factors. In terms of the factor tree, prime factors can be easily understood.
Practice Math Online with Unlimited Questions provided in 5th Grade Math Activity Sheets and become a blossoming mathematician in no time.
How to find Prime Factors of a Number using the Tree Method?
Tree method factorization is a straightforward method. The below provided guidelines in order to write down the prime factors using the tree method. They are,
- First, take the given number as the root of the tree.
- Next, write the factors of the given number as branches of the tree. You can break the number as any of the factors.
- Then factorize the composite numbers and write the factors pairs as the branches.
- You can do this process until you get the prime factors.
Finding Prime Factors Examples
Example 1:
Find the Prime Factors of the below-given Numbers,
(i) 8 (ii)4 (iii)13 (iv)14
Solution:
(i)Given Value is 8
Firstly, write the factors of 8 i.e. 4*2
As 4 is not a prime number we will write 4 again in terms of its factors i.e. 2*2. Therefore, 8 can be expressed in terms of prime factors as 2.
Now, pick the prime numbers among the factor list. Therefore, prime factors of 8 are 2
(ii) 4
Writing 4 in terms of factorization is 2×2.
So, 2 is a prime factor of 4.
(iii) 13
We can write 13 in terms of the factors as 1×13 and 13×1. Since 1 is neither prime nor composite number 13 is the Prime factor.
(iv) 14
Given Value is 14
We can express 14 in terms of factors as 2* 7 or 14*1
However, we will consider 2 and 7 as prime factors but not 14 and 1 as 14 is not a prime number.
Example 2:
Find the Prime Factors of 27 using the Factor Tree Method?
Solution:
The given value is 27, using the Factor Tree Method we can find the prime factors.
First, 27 is factored into two factors 3 and 9. 9 is again factored and written as factors of 3 and 3.
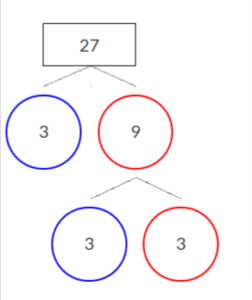
So, Writing the Prime Factors of 27 we have 3x3x3.
Example 3:
Find the Prime Factors of 56 using the Factor Tree Method.
Solution:
Given the value is 56,
Now, we will find the prime factors using the Factor Tree Method.
First, split the number given in to any of two factors. 56 is factored into two factors 2 and 28. 28 is again factorized into two factors 2 and 14. Now on splitting 14 further and writing it as multiples of numbers it might be 7 x 2.
The below tree structure formed for number 56 prime factors.
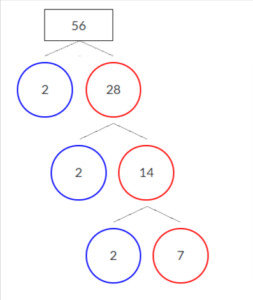
So, therefore the prime factor of 56 is 2x2x2x7.
Example 4:
Find the Prime Factors 216 using the Factor Division method?
Solution:
Given the value is 216, we can find the prime factors using the division method.
The division method consists of very easy and basic algorithms.
In this method, first, we have to check each number by dividing the composite number.
To get the prime factors of 216, we have to start by dividing them by prime numbers.
216 ÷108 = 2
108 ÷ 54 = 2
54 ÷ 27 = 2
27 ÷ 9 = 3
9 ÷ 3 = 3
3 ÷ 1 = 3
Therefore, the Prime Factor of 216 using the division method is 2 x 2 x 2 x 3 x 3 x 3= 23 x 33
