The Questions given in Quadrilaterals Practice Test makes it easy for you to understand the various kind of questions framed on the topic. Answer the Quiz Questions on Quadrilaterals on your own and then verify with the answers to understand your grip on the concept. Here will you find formulas for finding the area, perimeter of different quadrilateral shapes such as Parallelogram, Rhombus, Rectangles, Squares, etc.
Step by Step Solutions given in the Quadrailterals Practice Test makes it easy for you to get a clear idea of the concepts as well as helps you attempt the exams with utmost confidence. 5th Grade Students not just will develop strong fundamentals of the concept useful for higher classes but also develops problem-solving ability.
Also, Refer:
Quadrilaterals Practice Worksheet
Example 1:
If the perimeter of a square ABCD is 64 units. Find the number of units in BD?
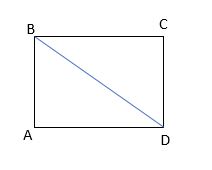
Solution:
Given,
The perimeter of a square=64
4a=64
a=64/4=16
Hence All sides of a square=16 units
By the Pythagoras theorem,
BC2 + CD2= BD2
162 + 162=BD2
256+256=BD2
512=BD2
BD=\(\sqrt{ 512 }\)
=22.6274
Hence, BD=22.6274 units.
Example 2
In the parallelogram given below, find AD?
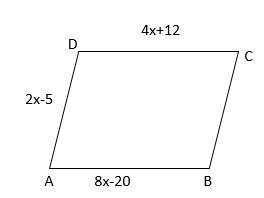
Solution:
We know that opposite sides are parallel and equal in length.
4x+12=8x-20
8x-4x=20+12
4x=32
x=8
2x-5=2(8)-5
=16-5
=11
Hence, AD=11
Example 3
If the area of a rhombus is 80 cm2, and the length of one of its diagonals is 4cm, what must be the length of the other diagonal?
Solution:
Given,
Area of the rhombus=80 cm2
length of diagonal=4 cm
We know the formula,
Area of rhombus=d1.d2/2
80=4.d2/2
160=4.d2
d2=160/4=40 cm
Hence, the length of the other diagonal is 40 cm
Example 4
In the parallelogram ABCD, find <B,<C,<D ?
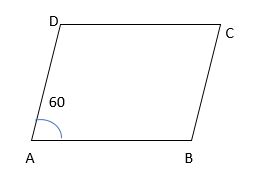
Solution:
Given <A=60
In a parallelogram, adjacent angles are supplementary
In the given parallelogram ABCD, <A,<B are supplementary
<A + <B=180
<B=180-60=120
We know that opposite angles are congruent.
<c=<A, <B=<D
<c=60, <D=120
Hence, the measures of <B,<C,<D are 120,60,120.
Example 5
The perimeter of the parallelogram ABCD is 20 units and the length of the side AB is 6 units, find the length of other sides of the parallelogram.
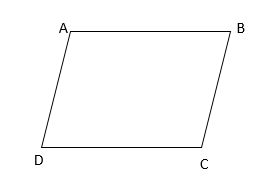
Solution:
Given,
The perimeter of the parallelogram is 20 units.
i.e., AB + BC + CD + AD = 20 —–> (1)
Because it is a parallelogram, the length of opposite sides must be equal. So, we have
AB = CD
AD = BC
Because AB = 6 units and AB = CD, we can have
Then, we have
From eq (1)—–> 6 + BC + 6 + AD = 20
12 + BC + AD = 20
Subtract 12 from both sides.
BC + AD = 8
Because AD = BC, we can have
AD + AD = 8
2 ⋅ AD = 8
Divide both sides by 2.
AD = 4
Then, the length of the CD is also 4 units.
Hence, the length of CD is 6 units, AD and BC are 4 units each.
Example 6
In the parallelogram given below, AO = x + 40, OC = 2x + 18. Find the length of AO and OC.
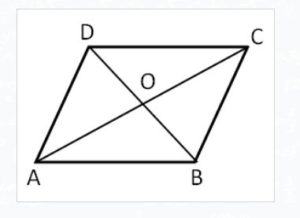
Solution:
According to the properties of parallelogram, the diagonals bisect each other.
So, we have AO =OC
x + 40 = 2x + 18
2x – x = 40 – 18
x = 22
The length of AO is
AO = x + 40
AO = 22 + 40
AO = 62
The length of OC is
OC = 2x + 18
OC = 2⋅ 22 + 18
OC = 44 + 18
OC = 62
Hence, the lengths of AO and OC are 62 units each.
Example 7
The figure below is the rhombus ABCD with diagonals drawn. AE=\(\frac { 3 }{ 4 } \) x and EC=x-5. Find the value of x?
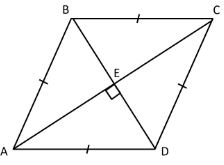
Solution:
Given,
AE=\(\frac { 3 }{ 4 } \) x
EC=x-5
Since the diagonals bisect each other
\(\frac { 3 }{ 4 } \) x =x-5
3x=4x-20
x=20
Example 8
ABCD is a rhombus.\(\overline{BC}\)=20 and\(\overline{BD}\)=20. Find AC.
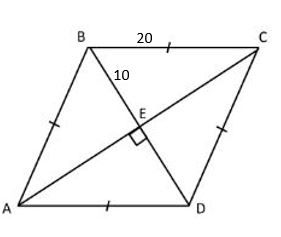
Solution:
Given,
\(\overline{BC}\)=20 and
\(\overline{BD}\)=10
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle AED to find the length of diagonal \(\overline{AC}\)=20
Because the diagonals bisect each other, we know:
\(\overline{AD}\)=20
\(\overline{ED}\)=5
Using the Pythagorean Theorem, a2+b2=c2
\(\overline{AE}\)2 + 5 2=20 2
\(\overline{AE}\)2 =400 – 25
\(\overline{AE}\)2 =375
\(\overline{AE}\)=19.36
\(\overline{AC}\)=38.72
Example 9
In a parallelogram below, find the length of sides GJ and HI?
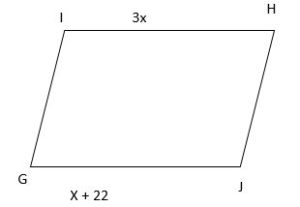
Solution:
According to the properties of the parallelogram, the length of opposite sides is equal.
Length of GJ=Length of IH
x+22=3x
2x=22
x=11
Length of IH=3x
=3(11)
=33
Therefore, the length of GJ and IH is 11,33.
Example 10
The angles of the quadrilateral are 700,800,1100. Find the fourth angle of the quadrilateral?
Solution:
Let the fourth angle be x.
We know that sum of all angles in the quadrilateral is 3600
70+80+110+x=360
260+x=360
x=360-260
x=100
