Practice Test on Linear Inequation has different types of questions. Students can test their skills and knowledge on linear inequations problems by solving all the provided questions on this page. The questions are mainly related to inequalities and finding the solution to the given inequation and draw a graph for the obtained solution set. You can easily draw a graph on a numbered line.
1. Write the equality obtained?
(i) On subtracting 1 from each side 3 > 7
(ii) On adding 3 to each side 12 < 5
(iii) On multiplying (-2) to each side 11 < 4
(iv) On multiplying 4 to each side 15 > 2
Solution:
(i) 3 – 1 > 7 – 1
2 > 6
(ii) 12 + 3 < 5 + 3
15 < 8
(iii) 11 x (-2) 4 x (-2)
-22 < -8
22 > 8
(iv) 15 x 4 > 2 x 4
60 > 8
2. Write the word statement for the following?
(i) x ≥ 15
(ii) x < 2
(iii) x ≤ -5
(iv) x > 16
(v) x ≠ 6
Solution:
(i) The variable x is greater than equal to 15. The possible values of x are 15 and more than 15.
(ii) The variable x is less than 2. The possible values of x are less than 2.
(iii) The variable x is less than and equal to -5. The possible values of x are less than -5.
(iv) The variable x is greater than 16. The possible values of x are more than 16.
(v) The variable x is not equal to 6. The possible values of x are all real numbers other than 6.
3. Find the solution set for each of the following inequations. x ∈ N
(i) x + 5 < 12
(ii) x – 6 > 5
(iii) 5x + 10 ≥ 17
(iv) 2x + 3 ≤ 6
Solution:
(i) x + 5 < 12
Subtract 5 from both sides.
x + 5 – 5 < 12 – 5
x < 7
Replacement set = {1, 2, 3, 4, 5 . .}
Solution set S = {1, 2, 3, 4, 5, 6}
(ii) x – 6 > 5
Add 6 to both sides.
x – 6 + 6 > 5 + 6
x > 11
Replacement set = {1, 2, 3, 4, 5 . .}
Solution set S = {12, 13, 14, 15, . . . }
(iii) 5x + 10 ≥ 17
Subtract 10 from both sides.
5x + 10 – 10 ≥ 17 – 10
5x ≥ 7
Divide 5 by each side.
5x/5 ≥ 7/5
x ≥ 1.4
Replacement set = {1, 2, 3, 4, 5 . .}
Solution set S = {2, 3, 4, 5 . . .}
(iv) 2x + 3 ≤ 6
Subtract 3 from both sides of the inequation
2x + 3 – 3 ≤ 6 – 3
2x ≤ 3
Both sides of the inequation divide by 2.
2x/2 ≤ 3/2
x ≤ 1.5
Replacement set = {1, 2, 3, 4, 5 . .}
Solution set S = {1, 1.5}
4. Find the solution set for each of the following inequations and represent it on the number line.
(i) 3 < x < 10, x ∈ N
(ii) 3x + 2 ≥ 6, x ∈ N
(iii) 3x/2 < 5, x ∈ N
(iv) -4 < 2x/3 + 1 < – 2, x ∈ N
Solution:
(i) 3 < x < 10, x ∈ N
The two cases are 3 < x and x < 10
It can also represent as x > 3 and x < 10
Replacement set = {1, 2, 3, 4, 5 . .}
The solution set for x > 3 is 4, 5, 6, 7 . . . i.e P = {4, 5, 6, 7 . . .}
And the solution set for x < 10 is 1, 2, 3, 4, 5, 6, 7, 8, 9 i.e Q = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Therefore, solution set of the given inequation = P ∩ Q = {4, 5, 6, 7, 8, 9}
Let us represent the solution set graphically.
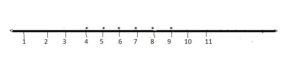
The solution set is marked on the number line by dots.
(ii) 3x + 2 ≥ 6, x ∈ N
Subtract 2 from both sides
3x + 2 – 2 ≥ 6 – 2
3x ≥ 4
Divide each side by 3
3x/3 ≥ 4/3
x ≥ 1.33
Replacement set = {1, 2, 3, 4, 5 . .}
Solution set S = {2, 3, 4, 5, . . }
Let us represent the solution set graphically.
![]()
The solution set is marked on the number line by dots.
(iii) 3x/2 < 5, x ∈ N
Multiply both sides by 2.
3x/2 x 2 < 5 x 2
3x < 10
divide both sides by 3
3x/3 < 10/3
x < 3.33
Replacement set = {1, 2, 3, 4, 5 . .}
Solution Set S = {1, 2}
Let us represent the solution set graphically.
![]()
The solution set is marked on the number line by dots.
(iv) -4 < 2x/3 + 1 < – 2, x ∈ N
The two cases are -4 < 2x/3 + 1 and 2x/3 + 1 < – 2
Case I: -4 < 2x/3 + 1
Subtract 1 from both sides
-4 – 1 < 2x/3 + 1 – 1
-5 < 2x/3
Multiply each side by 3
-5 x 3 < 2x/3 x 3
-15 < 2x
Divide each side by 2
-15/2 < 2x/2
-7.5 < x
x > 7.5
Replacement Set = {1, 2, 3, 4, 5 . .}
Solution Set P = {8, 9, 10, 11 . . . }
Case II: 2x/3 + 1 < – 2
Subtract 1 from both sides
2x/3 + 1 – 1 < – 2 – 1
2x/3 < -3
Multiply 3 to both sides
2x/3 x 3 < -3 x 3
2x < -9
Divide both sides by 2
2x/2 < -9/2
x < -4.5
4.5 > x
Replacement set = {1, 2, 3, 4, 5 . .}
Solution set Q = {1, 2, 3}
Therefore, required solution set S = P ∩ Q
S = Null
5. Find the solution set for each of the following and represent the solution set graphically?
(i) x – 6 < 4, x ∈ W
(ii) 6x + 2 ≤ 20, x ∈ W
(iii) 7x + 3 < 5x + 9, x ∈ W
(iv) 3x – 7 > 5x – 1, x ∈ I
Solution:
(i) x – 6 < 4, x ∈ W
Add 6 to both sides
x – 6 + 6 < 4 + 6
x < 10
Replacement set = {0, 1, 2, 3, 4, 5, 6, …}
Therefore, solution set S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Let us represent the solution set graphically.
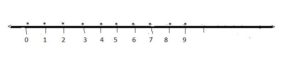
The solution set is marked on the number line by dots.
(ii) 6x + 2 ≤ 20, x ∈ W
Subtract 2 from both sides
6x + 2 – 2 ≤ 20 – 2
6x ≤ 18
Divide each side by 6
6x/6 ≤ 18/6
x ≤ 3
Replacement set = {0, 1, 2, 3, 4, 5, 6, …}
Therefore, solution set S = {0, 1, 2, 3}
Let us represent the solution set graphically.
![]()
The solution set is marked on the number line by dots.
(iii) 7x + 3 < 5x + 9, x ∈ W
Move variables to one side and constants to other side of inequation
7x – 5x < 9 – 3
2x < 6
Divide each side by 2
2x/2 < 6/2
x < 3
Replacement set = {0, 1, 2, 3, 4, 5, 6, …}
Therefore, solution set S = {0, 1, 2}
Let us represent the solution set graphically.
![]()
The solution set is marked on the number line by dots.
(iv) 3x – 7 > 5x – 1, x ∈ I
Move variables to one side and constants to another side of inequation
-7 + 1 > 5x – 3x
-6 > 2x
divide 2 by each side
-6/2 > 2x/2
-3 > x
Replacement set ={ . . . -4, -3, -2, -1, 0, 1, 2, 3, . . .}
Solution set = { -2, -1, 0, 1, 2, . . . }
Let us represent the solution set graphically.
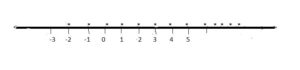
The solution set is marked on the number line by dots.