A hexagon is a polygon that consists of 6 sides that are connected with line segments. The regular hexagon is the polygon that has all the sides and also the angles are equal. The sides of the regular hexagon are congruent. Now, let us discuss the perimeter and area of Regular Hexagon with examples and images. We have given regular hexagon problems along with answers and explanations.
All the 9th Grade Math concepts, worksheets, and also problems are given on our website for free cost. Check out all the concepts you want to learn to get good marks in the exam. The image of the hexagon is given below.
Area and Perimeter of Regular Hexagon
Now, go through the below article to know the Perimeter and Area of a Regular Hexagon.
Perimeter of Regular Hexagon Formula
The Perimeter of a hexagon is the sum of all side lengths of it. The regular hexagon consists of 6 sides. Multiplying the side length of the hexagon with 6 gives you the perimeter of the hexagon. If you consider the side length of the hexagon as a, then the perimeter of a regular hexagon becomes P = 6 × a.
The perimeter of a Hexagon = 6a.
See More:
Area of Regular Hexagon Formula
The area of the hexagon is the space or region inside the boundary of the hexagon. To calculate the area of the hexagon, we need to make the hexagon into six isosceles triangles. Then by calculating the area of one isosceles triangle we can multiply all the 6 triangles and can find the total area of the polygon.
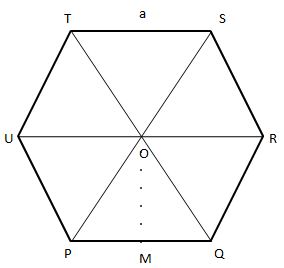
Area of the Hexagon Formula Derivation
Firstly, take one of the triangles and draw a middle line from the midpoint of the base that forms a right angle. Let us consider the base of the triangle as a and the side length of the polygon is h.
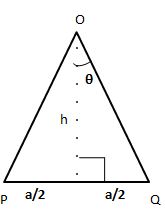
The sum of all exterior angles present on the triangle is equal to 360 degrees. Here, ∠POQ = 360/6 = 60°.
Therefore, θ = 30°.
As we know that the tan of an angle is opposite side by adjacent side,
Therefore, tan θ = (a/2)/h
tan 30 = (a/2)/h
√3/3 = (a/2)/h
h = (a/2) × (3/√3)
The area of a triangle = bh/2
The area of a triangle = 1/2 × a × a/2 × (3/√3)
= (3/√3) (a2/4)
Area of the hexagon = 6 x Area of Triangle
Area of the hexagon = 6 x (3/√3) (a2/4)
Therefore, the area of the hexagon = 3√3/2 × a2
Also, check:
- Perimeter and Area of Irregular Figures
- Perimeter and Area of Square
- Perimeter and Area of Rectangle
Perimeter and Area of Regular Hexagon Examples
Check out the below examples and know-how to find the area and perimeter of the regular hexagon.
Question 1.
Calculate the area and perimeter of a regular hexagon whose side is 8.2cm.
Solution:
Given that the side of the hexagon is 8.2 cm.
Area of a Hexagon = 3√3/2 × a2
Area of a Hexagon = 3√3/2 × (8.2)2 = 174.68952 cm2
Perimeter of the hexagon = 6a = 6 × 8.2 = 49.2 cm
Therefore, the area = 174.68952 cm2 and perimeter = 49.2 cm
Question 2.
The perimeter of a hexagonal is 48 cm. Find the area of the board?
Solution:
Given that the perimeter of a hexagonal is 48 cm.
The perimeter of a Hexagon = 6a
48 cm = 6a
a = 48/6 cm
a = 8 cm.
The Area of a Hexagon = 3√3/2 × a2 = 3√3/2 × 82 = 166.27 cm
Therefore, the Area of a Hexagon is 166.27 cm2 when the perimeter of the hexagon is 8 cm.
Question 3.
If the area of a regular hexagon is 48√3 cm2, find its perimeter.
Solution:
Given that the area of a regular hexagon is 48√3 cm2,
Let the side of a regular hexagon be a.
The Area of a Hexagon = 3√3/2 × a2
So, 3√3/2 × a2 cm2 = 48√3 cm2,
Divide the above equation with √3 into both sides.
3/2 × a2 = 48
a2 = 48 × 3/2
a2 = 72
a = 8.48 cm
Therefore, perimeter = 6a = 6 × 8.48 = 50.88 cm
FAQs on Area and Perimeter of Regular Hexagon
1. Define the area of the Regular Hexagon
The area of the Regular Hexagon is defined as the closed region between the hexagon.
2. What is the formula for the area of a Regular Hexagon?
The formula for the area of a Regular Hexagon is (3√3/2) × (a2)
3. Define the perimeter of the Regular Hexagon
The perimeter of the Regular Hexagon is the total area covered around the hexagon. By adding all the side lengths of the hexagon.
4. What is the formula for the perimeter of a Regular Hexagon?
The formula for the perimeter of a Regular Hexagon is 6a as the hexagon consists of six sides.
