Perimeter and Area of Mixed Figures – Definition, Facts, Examples | How do you find the Perimeter and Area of Combined Figures?

Let’s learn how to find the Perimeter and Area of Mixed Figures. We will get mixed figures with the combination of several shapes. The mixed figures may be a combination of any shapes like triangle and square, square and rectangle, triangle and pyramid, etc. This article completely explains the formulas for perimeter and area of the different mixed figures, steps on how to find the area and perimeter of combined figures. 9th Grade Math students can get different examples with their explanations step by step with relevant images for better understanding.

Mixed Figures – Definition

When we add different shapes to form a combined shape, we can see the different shapes. The shape which is the combination of different shapes is known as mixed figures. Below is an example of a mixed figure.

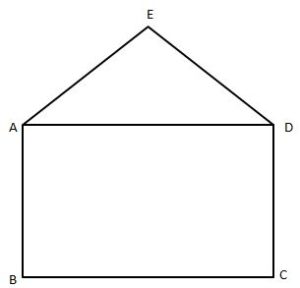
From the above figure, ABCD is a rectangle and ABE is a triangle. By combining both figures, we got a new figure ABCDE.

How to find Perimeter and Area of Mixed Figures?

Follow the below procedure to find the perimeter and area of mixed figures. The step-by-step process to find the area and perimeter is given separately below.

How to Find Area of Mixed Figures?

Step 1: Firstly, find out the shape.
Step 2: If you identify the individual shapes then find the area separately.
Step 3: Then, add the total area to find the complete answer.
Step 4: Finally, note down the answer in square units.

Also, check:

• Perimeter and Area of Irregular Figures
• Perimeter and Area of Square
• Perimeter and Area of Rectangle

How to Find the Perimeter of Mixed Figures?

The perimeter of the mixed figures can find by adding the total side lengths of the shape. If rectangle and square are two shapes then add the lengths of four sides.

Perimeter and Area of Mixed Shapes Examples

Example 1: The length and breadth of a rectangular field are 16 cm and 12 cm respectively. Two right-angled isosceles triangles are constructed outside the rectangular field, with the longer sides as the hypotenuses. On the 12 cms sides of the rectangular field, two equilateral triangles are constructed outside. Find the total area and perimeter of the figure.

Solution: The figure consists of the following.

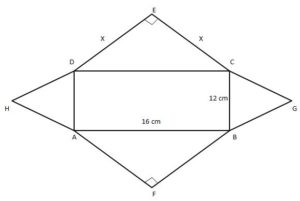
(i) The rectangular field ABCD, whose area = 16 × 12 cm²  = 192 cm²
(ii) Two equilateral triangles ADH and BCG. For each, area = √3/4 × 12 cm²  = 3 √3 cm²
(iii) Two isosceles right-angled triangles CDE and ABF, whose areas are equal.
According to Pythagoras’ theorem, if CE = ED = x then x²  + x²  = (16)²  cm²  or 2x²  = 256 cm². Therefore, x = 8√2 cm.
Therefore, the area of the ∆CDE = 1/2 CE × DE = 1/2 x²  = 1/2 (8√2)² cm² = 64 cm²
Therefore, area of the figure = area of the rectangular field ABCD + 2 × area of the ∆BCG + 2 × area of the ∆CDE
= (192 + 2 × 3 √3 + 2 × 64) cm² = 1920√3 cm² =
The perimeter of the figure = length of the boundary of the figure
= AF + FB + BG + GC + CE + ED + DH + HA
= 4 × CE + 4 × BG
= (4 × 8√2 + 4 × 12) cm
= 93.12 cm

Example 2. The dimension of a field is 220 m × 160 m. The field is to be converted into a garden after some days, leaving a path 10 m broad around the garden. Find the total cost of making the new garden if the cost per square meter is Rs 24.

Solution:

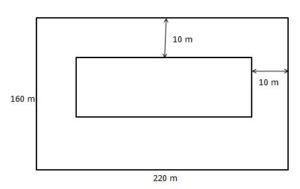
For the garden, length = (220 – 2 × 10) m = 200 m, and Breadth = (160 – 2 × 10) m = 140 m.
Therefore, area of the garden = 200 m × 140 m = 28000 m².
Therefore, the total cost of making the garden = 28000 × Rs 24 = 672000

Example 3. A square-shaped piece of paper is made into two pieces along a line joining a corner and a point on an opposite edge. If the ratio of the areas of the two pieces is 6:2, find the ratio of the perimeters of the smaller piece and the original piece of paper.

Solution:

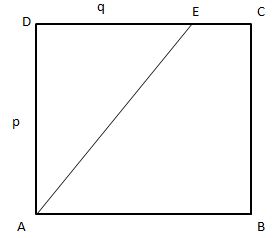
Let ABCD be the square-shaped piece of paper. Let its side measure a unit.
It is cut along AE. Let DE = q units
Area of the ∆EDA = 1/2 (AD × DC) = 1/2 pq square units.
Area of the square ABCD = p² square units.
According to the question,
(Area of the quadrilateral ABCE/ Area of the ΔEDA) = 6/2
(Area of the quadrilateral ABCE/ Area of the ΔEDA) + 1 = 8/2
(area of the quadrilateral ABCE + area of the ΔEDA)/area of the ΔEDA = 8/2
(Area of the quadrilateral ABCD/ Area of the ΔEDA) = 4
p²/(pq/2) = 4
2p/q = 4
p = 2q
q = p/2
According to Pythagoras’ theorem,
AE² = AD² + DE²
Therefore, AE² = p² + q²
= p² + (p/2)²
= p² + 1/4 (p²)
= 5/4 (p²)
Therefore, AE² = √5/2p.
Now, the perimeter of the ΔEDA/perimeter of the square ABCD = (ED + AD + AE)/4p
= (p/2 + p + √5p/2)/4p
= [(3+√5)p/2]/4p
= (3+√5)/8
= (3+√5) : 8.

Example 4. From a 40 cm × 20 cm board having an F-shaped block is cut out as given in the below figure. What is the area of the face of the remaining board? Also, find the length of the boundary of the board or block.

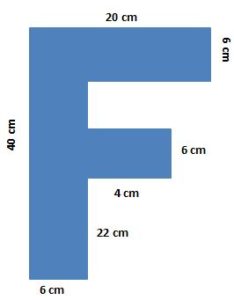
Solution:
The given figure is the combination of three rectangular blocks.

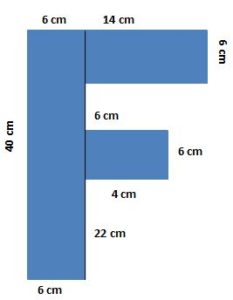
Therefore, area of a face of the block = 40 × 6 cm² + 6 × 4 cm² + 14 × 6 cm²
= 240 cm² + 28 cm² + 84 cm²
= 352 cm²
Area of a face of the uncut board = 40 × 20 cm²
= 800 cm²
Therefore, the area of the face of the remaining board = 800 cm² – 352 cm²  = 448 cm²
Required length of the boundary = (40 + 6 + 22 + 4 + 6 + 4 + 6 + 14 + 6 + 20) cm = 128 cm