In mathematics, a pattern is a repeated arrangement of shapes, colors, numbers, and so on. These are also called a sequence. Students can get the different types of patterns and simple tricks to solve them in the following sections. Also, find the solved example questions on number patterns explained clearly on this page.
Also, Check:
Patterns in Mathematics
We can find many patterns in our daily life. We already know that pattern is an arrangement of objects, numbers, colors, images, in an order. If the set of numbers are related to each other in a specific rule then that rule is called a pattern. Patterns are finite or infinite numbers. Sometimes, patterns are also called a sequence.
The different types of patterns are number patterns, image patterns, logic patterns, letter patterns, word patterns, etc. Some of the examples of simple patterns are here.
Examples:
Set of Natural Numbers – 1, 2, 3, 4, . .
Set of even numbers – 2, 4, 6, 8, 10, . .
Set of odd numbers – 1, 3, 5, 7, . . .
Different Types of Patterns in Math
The three important types of patterns in mathematics are along the lines:
- Repeating Pattern: A pattern in which the rule keeps repeating over and over is called a repeating pattern.
- Growing Pattern: If the numbers are present in the increasing form, then the pattern is a growing pattern.
- Shrinking Pattern: If the numbers are in the decreasing form, then it is a shrinking pattern.
The types of number patterns are arithmetic pattern, geometric pattern and Fibonacci pattern.
Tips & Tricks on How to Solve Patterns in Math?
The following are the simple tricks to compute the pattern. Students who are willing to create a new pattern can go through these steps.
1. Finding Missing Term: Let us take a pattern 2, 3, 5, 7, . . by observing this pattern, we can say that it is a pattern of prime numbers. The prime number that occurs after 7 is 11. So, the next term will be 11.
2. Difference Rule: Sometimes, it is easy to find the difference between two successive terms. Let us take a pattern 0, 5, 10, 15, . . . Here, the difference of successive pairs is 5. So, add 5 to the last term to get the next term.
Examples of Patterns in Math
Question 1:
Find the next image.
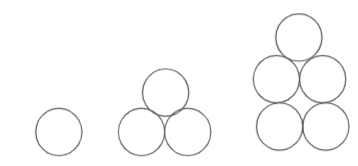
Solution:
In the given pattern,
1st image has 1 circle
2nd image has 3 circles
3rd image has 5 circles
So, it is a set of odd numbers
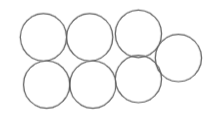
The next image must have 7 circles.
Question 2:
Find the next image of the following pattern

Solution:
In the given pattern,
1st image has 1 square
2nd image has 2 stars
3rd image has 3 squares
So, here we have square and stars one after the other and a set of natural numbers.
The next image must have 4 stars.

Question 3:
Write the next 3 terms of the pattern 7, 63, 619, 6175, . . .
Solution:
Given pattern is
7, 63, 619, 6175, . . .
By observing the pattern, we can say that
7 = 1 x 5 + 2
63 = 12 x 5 + 3
619 = 123 x 5 + 4
6175 = 1234 x 5 + 5
In, the same the next 3 terms of the pattern can be
5th term = 12345 x 5 + 6 = 61725 + 6 = 61731
6th term = 123456 x 5 + 7 = 617280 + 7 = 617287
7th term = 1234567 x 5 + 8 = 6172835 + 8 = 6172843
Therefore, the next three terms of the pattern are 61731, 617287, 6172843.
Question 4:
Complete the given series
(i) 1, 4, 9, 16, 25, . . .
(ii) 5, 55, 555, 5555, . .
(iii) 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, . . .
(iv) 7, 13, 19, 25, . .
Solution:
(i) The given pattern is 1, 4, 9, 16, 25, . . .
By observing the pattern, we can say that
1st term = 1² = 1
2nd term = 2² = 4
3rd term = 3² = 9
4th term = 4²= 16
5th term = 5² = 25
6th term = 6² = 36
7th term = 7² = 49
8th term = 8² = 64
So, the series is 1, 4, 9, 16, 25, 36, 49, 64
(ii) The given pattern is 5, 55, 555, 5555, . .
By observing the pattern, we can say that every term is a divided of 5.
1st term = 5 ÷ 5 = 1
2nd term = 55 ÷ 5 = 11
3rd term = 555 ÷ 5 = 111
4th term = 5555 ÷ 5 = 1111
So, the remaining terms will be
5th term = 11111 x 5 = 55555
6th term = 111111 x 5 = 555555
7th term = 1111111 x 5 = 5555555
So, the series is 5, 55, 555, 5555, 55555, 55555, 555555, 5555555
(iii) The given pattern is 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, . . .
By observing the pattern, we can say that each number written those many times
So, the series is 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7
(iv) The given pattern is 7, 13, 19, 25, . .
Find the difference between two successive terms
13 – 7 = 6
19 – 13 = 6
25 – 19 = 6
So, 5th term = 4th term + 6
= 25 + 6 = 31
6th term = 31 + 6 = 37
7th term = 37 + 6 = 43
So, the series is 7, 13, 19, 25, 31, 37, 43
Frequently Asked Questions on Patterns
1. What is a pattern rule in math?
In general, a numerical pattern is a series of numbers that is created based on a formula or method called the pattern rule. Pattern rule can use any number of mathematical operations to describe the relationship between the consecutive numbers.
2. What is a number pattern?
Number pattern is also a pattern that has numbers and develops the relationship between all numbers. The types of number patterns are arithmetic, geometric, cube numbers, square numbers, triangular numbers, Fibonacci numbers.
3. What are examples of patterns?
Some examples of patterns are 240, 120, 60, . .
The relation between numbers is 1st term divided by 2 gives the 2nd term
So, the next terms are 30, 15, 7.5, 3.75, . .
Another example is 8, 16, 24, . .
The relation between numbers is all the numbers are multiples of 8
So, the next terms are 32, 40, 48, . .
