Parallelogram consists of a flat shape that has two opposite & parallel sides with equal length. The parallelogram has four sides and also it is called a quadrilateral. The pair of parallel sides are always equal in length of a parallelogram. Furthermore, the interior opposite angles also equal in measurement. While adding the adjacent angles of a parallelogram, you will get 180 degrees.
The area of the parallelogram always depends on its base and height. Also, the perimeter of the parallelogram depends on the length of its four sides.
List of Parallelogram Concepts
Have a glance at the list of Parallelogram Concepts available below and use them for your reference. All you need to do is simply tap on the quick links and avail the underlying concept within. Practice as much as you can and solve all the problems easily.
- Properties of a Rectangle Rhombus and Square
- Problems on Parallelogram
- Practice Test on Parallelogram
Parallelogram Definition
A parallelogram called a quadrilateral that has two pairs of parallel sides. The interior angles of the parallelogram on the same side of the transversal are supplementary. The sum of all the interior angles becomes 360 degrees in a parallelogram.
A rectangle and square also consist of similar properties of a parallelogram. If in case, the sides of the parallelogram become equal, then it treats as a rhombus. Or else, if a parallelogram has one parallel side and the other two sides are non-parallel, then it treats as a trapezium.
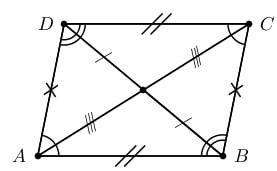
From the above figure, ABCD is a parallelogram, where CD || AB and BC || AD. Also, CD = AB and BC = AD.
And, ∠A = ∠C & ∠B = ∠D
Also, ∠A & ∠D are supplementary angles. Because ∠A & ∠D are interior angles present on the same side of the transversal. Similarly, ∠B & ∠C are supplementary angles.
Therefore, ∠B + ∠C = 180, ∠A + ∠D = 180.
Shape of Parallelogram
A parallelogram shape is a two-dimensional shape. It consists of four sides and two pairs of parallel sides. All the parallel sides of the Parallelogram are equal in length. Also, the interior angles of the parallelogram should always equal.
Angles of Parallelogram
The Parallelogram has four angles. Its opposite interior angles always equal and the angles on the same side of the transversal are always supplementary with each other. When you add the same side of the transversal angles, you can get 180 degrees. Furthermore, the sum of the interior angles is 360 degrees.
Properties of Parallelogram
Check the below properties of a parallelogram and solve the related problems easily by applying the same. They are as follows
- The opposite angles of a parallelogram are congruent.
- Also, the opposite sides are parallel and congruent
- The consecutive angles are supplementary
- Furthermore, The two diagonals bisect each other
- If one angle of a parallelogram is a right angle, then all other angles are right angles.
- Parallelogram law: The sum of squares of all the sides of a parallelogram is always equal to the sum of squares of its diagonals.
- Each diagonal bisects the parallelogram into two congruent triangles.
Area of Parallelogram
The area of the Parallelogram totally depends on the Base and height of the Parallelogram.
The area of the Parallelogram can be calculated as Area = Base × Height
Perimeter of Parallelogram
The perimeter of a parallelogram is calculated as the total distance of the boundaries of the parallelogram. By knowing the length and breadth of the parallelogram, we can get the perimeter of a parallelogram.
Perimeter = 2 (a+b) units where a and b are the length of the sides of the parallelogram.
Types of Parallelogram
Depends on the angles and sides of the Parallelogram, mainly four types of Parallelogram are considered.
Let ABCD is a Parallelogram,
1. If AB = BC = CD = DA are equal, then it is called a rhombus. The properties of the rhombus and parallelogram are equal.
2. Rectangle, Square are also types of the parallelogram.
Parallelogram Theorems
Theorem: Prove that in a parallelogram, the opposite sides are equal; the opposite angles are equal; diagonals bisect each other.
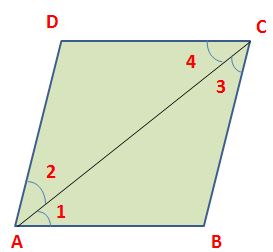
Proof:
Let ABCD be a parallelogram. Draw its diagonal AC.
In ∆ ABC and ∆ ACD, ∠1 = ∠4 (alternate angles)
∠3 = ∠2 (alternate angles)
and AC = CA (common)
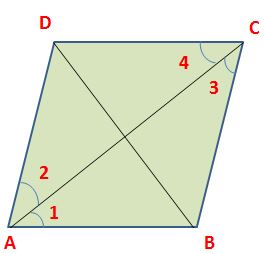
Therefore, ∆ ABC ≅ ∆ ACD (by ASA congruence)
⇒ AB = CD, BC = AD and ∠B = ∠D.
Similarly, by drawing the diagonal BD, we can prove that
∆ ABD ≅ ∆ BCD
Therefore, ∠A = ∠C
Thus, AB = CD, BC = AD, ∠A = ∠C and ∠B = ∠D.
This proves (i) and (ii)
In order to prove (iii) consider parallelogram ABCD and draw its diagonals AC and BD, intersecting each other at O.
In ∆ OAB and ∆ OCD, we have
AB = CD [Opposite sides of a parallelogram]
∠AOB = ∠ COD [Vertically opposite angles]
∠OAB = ∠OCD [Alternate angles]
Therefore, ∆ OAB ≅ ∆ OCD [By ASA property]
⇒ OA = OC and OB = OD.
This shows that the diagonals of a parallelogram bisect each other.
Therefore, in a parallelogram, the opposite sides are equal; diagonals bisect each other; the opposite angles are equal.