In this article, you will learn about the Matrix multiplication or multiplication of matrices. Matrix multiplication is one of the operations it can be performed on the matrices in linear algebra. The multiplication of matrix A with matrix B is possible when both the matrices will be compatible. Matrix multiplication is a binary operation, that gives a matrix from two given matrices.
The multiplication of matrices is different from the multiplication of numbers. A matrix is a rectangular array that consists of numbers, expressions, letters, symbols, etc. which are arranged in rows and columns. The 10th Grade Math multiplication of matrices is clearly explained in this article below.
Also, Find:
What is the Multiplication of Matrices?
Matrix multiplication is one of the binary operations, the output of the matrix is also in matrix form only when two matrices are multiplied. In linear algebra, the multiplication of matrices is possible only when the matrices are compatible. Matrix multiplication is unlike arithmetic multiplication, it is not commutative, which means the multiplication of matrix A and B are given as AB cannot be equal to BA, i.e., AB ≠ BA. So, the order of matrix multiplication for multiplication is very important.
What is the Formula for Multiplication of Matrices?
The product of two matrices A and B is defined as if the number of columns of the A is equal to the number of rows of the B. The elements of the same order matrices are multiplied individually. If A = [aij] is an m × n matrix and B = [bjk] is an n × p matrix, then the product of the matrices A and B is the matrix c of order m × p. To get the (i, k)th element c of the matrix C, we take the ith row of A and kth column of B, multiply them element-wise and take the sum of all these products.
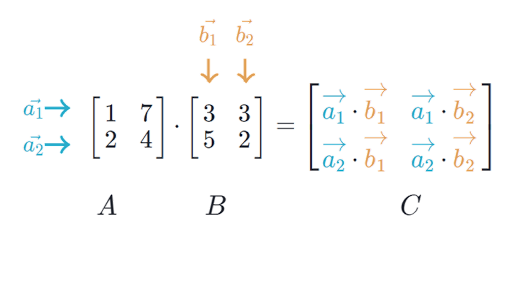
Types of Multiplication of Matrices
There are two different types of Multiplication of matrices available. They are Scalar Multiplication of Matrices and the other one is matrix multiplication which means multiplying a matrix by another matrix.
Scalar Multiplication: The term scalar multiplication refers to the product of a real number and a matrix. In a scalar multiplication of matrix, each entry in the matrix is multiplied by the given scalar.
Matrix Multiplication: Whenever we multiply a matrix by another one we need to find out the dot product of rows of the first matrix and columns of the second. If A = [aij]m x n and B = [bij]n x p are two matrices such that the number of columns of A = number of rows of B, then the product of A and B is Cm x p.
Rules for Multiplication of Matrices
When we do Matrix multiplication, we keep these two conditions in mind:
-
- The first condition is, that the number of columns of the first matrix in the multiplication process must equal the number of rows of the second matrix.
- Next, the result of the product will have the same number of rows as in the first matrix, and the same number of columns as in the second matrix.
Examples:
(i) Multiplying a 5× 3 matrix with a 3 × 5 matrix is valid and it gives a matrix of order 5× 5.
(ii) 6 × 1 matrix and 1 × 3 matrices are compatible; the product gives a 6 × 3 matrices.
(iii) Multiplication of a 6 × 3 matrices and 1 × 3 matrix is NOT possible.
How to Multiply Matrices?
You can understand the process of matrix multiplication by the technique first rows are multiplied by columns like element by element and then the rows are filled up. So, the following are the steps to perform the multiplying matrices:
- Step 1: Initially check the number of columns in the 1st matrix is equal to the number of rows in the 2nd matrix or not.
- Step 2: Next, multiply the elements of the ith row of the first matrix by the elements of the jth column in the second matrix. Now, Add the products. So the element that is in the ith row and jth column of the resultant matrix.
- Step 3: keep the added products in their positions.
In the resultant matrix, you can observe that the first element of the first row is obtained by multiplying the elements of the first row of the first matrix by the corresponding elements of the first column of the second matrix and then adding. To find the element in the ith row and jth column in the product matrix,
- Take the elements of the ith row of the first matrix.
- Take the elements of the jth column of the second matrix.
- Then multiply the respective elements.
- Add all the products.
Properties of Matrix Multiplication
The properties of multiplication are as given below. There are certain properties of matrix multiplication operation in linear algebra in mathematics. The properties are:
Non-Commutative Property: Matrix multiplication is non-commutative, i.e., for multiplication of two matrices A and B, AB ≠ BA.
Distributivity Property: The distributive property can be applied while multiplying matrices, i.e., A(B + C) = AB + BC, given that A, B, and C are compatible.
Product with Scalar Property: If the product of matrices A and B, AB is defined then, c(AB) = (cA)B = A(Bc), such that c is a scalar.
Transpose Property: The transpose property states that the product of matrices A and B can be given as, (AB)T = BTAT, where T denotes the transpose.
Complex Conjugate Property: This property states that, if A and B are complex entries, then (AB)* = B*A*
Associativity Property: Matrix multiplication is associative.If three matrices A, B, and C, such that the products (AB)C and A(BC) are defined, then (AB)C = A(BC).
Read More:
Questions on Multiplication of Matrices
Below are examples to solve with different tips and tricks. All the properties are used to solve the multiplication matrix problems. So, try to practice every problem to know how to solve the multiplication of matrices problems.
Problem 1: Multiply the given matrix by 2. The matrix is,
\( A = \left[
\begin{matrix}
1 & 0\cr
2 & 4\cr
\end{matrix}
\right]
\) What is the final value of Matrix?
Solution:
As given in the question,
The matrix A is \( A = \left[
\begin{matrix}
1 & 0\cr
2 & 4\cr
\end{matrix}
\right]
\)
Now, multiply given matrix by 2.
After, multiplication the matrix is \( A = \left[
\begin{matrix}
1 *2 & 0*2\cr
2*2 & 4*2\cr
\end{matrix}
\right]
\)
Therefore, the matrix value of A is \( A = \left[
\begin{matrix}
2 & 0\cr
4 & 8\cr
\end{matrix}
\right]
\)
Problem 2: Matrix A is of 4×1 order. Matrix B is of 1×3 order. Both the products of AB and BA are defined or not?
Solution:
In the given question,
The Matrix A is of order 4×1.
The Matrix B is of order 1×3.
The product AB will be defined as the number of columns of A is the same as the number of rows of the B.
By using the multiplication of matrices rule, the product matrix hence obtained is of order 4×3.
Next, the product BA is not defined as the number of columns of B is not equal to the number of rows of A.
So, we can say that the matrix multiplication is not commutative, AB is not necessarily equal to BA and sometimes one of the products may also be not defined.
Hence, the product AB is defined but not BA.
Problem 3: Find the value of 5A – 2B where \( A = \left[
\begin{matrix}
1 & 0\cr
0 & 1\cr
\end{matrix}
\right]
\) and \( B = \left[
\begin{matrix}
3 & 2\cr
4 & 7\cr
\end{matrix}
\right]
\)
Solution:
Given the matrices are \( A = \left[
\begin{matrix}
1 & 0\cr
0 & 1\cr
\end{matrix}
\right]
\) and \( B = \left[
\begin{matrix}
3 & 2\cr
4 & 7\cr
\end{matrix}
\right]
\)
Firstly, find the value of 5A.
To find the value of 5A, we need to multiply the value 5 with all the elements of matrix A.
\( 5A = \left[
\begin{matrix}
5*1 & 5*0\cr
5*0 & 5*1\cr
\end{matrix}
\right]
\) \( = \left[
\begin{matrix}
5 & 0\cr
0 & 5\cr
\end{matrix}
\right]
\)
Now, find the value of 2B.
\( 2B = \left[
\begin{matrix}
2*3 & 2*2\cr
2*4 & 2*7\cr
\end{matrix}
\right]
\) \( = \left[
\begin{matrix}
6 & 4\cr
8 & 14\cr
\end{matrix}
\right]
\)
Finally, find the value of 5A – 2B \( =\left[
\begin{matrix}
5 & 0\cr
0 & 5\cr
\end{matrix}
\right]
\) – \( \left[
\begin{matrix}
6 & 4\cr
8 & 14\cr
\end{matrix}
\right]
\)
\( = \left[
\begin{matrix}
5-6 & 0-4\cr
0-8 & 5-14\cr
\end{matrix}
\right]
\) \( = \left[
\begin{matrix}
-1 & -4\cr
-8 & -9\cr
\end{matrix}
\right]
\)
Therefore, the value of \( 5A – 2B = \left[
\begin{matrix}
-1 & -4\cr
-8 & -9\cr
\end{matrix}
\right]
\)
FAQ’s on Multiplication of Matrices
1. What is the Purpose of Matrix Multiplication?
The purpose of matrix multiplication is important for facilitating computations in linear algebra and is used for representing linear maps. In many areas of mathematics, it is an important tool, as well as in applied mathematics, statistics, physics, economics, and engineering.
2. When can we find the Product of Matrices?
Matrix multiplication is possible only if the matrices are compatible i.e., multiplying matrices is valid only if the number of columns of the first matrix is equal to the number of rows of the second matrix.
3. Is Matrix Multiplication Always Defined?
Matrix multiplication is possible only when the matrices are compatible. For the multiplication of matrices to exist the number of columns in the first matrix should be equal to the number of rows in the second matrix.
4. What are the different types of matrices?
There are many types of matrices that exist. However, the most commonly used are rectangular matrix, square matrix, rows matrix, columns matrix, scalar matrix, diagonal matrix, identity matrix, triangular matrix, null matrix, and the transpose of a matrix.
5. How can one multiply matrices together?
The multiplication of matrices can take place with the following steps:
1. The number of columns in the first one must the number of rows in the second one.
2. Now you must multiply the first matrix’s elements of each row by the elements belonging to each column of the second matrix.
3. Finally, add the products.
Summary
Multiplication of Matrices is similar to Multiplication of numbers. But the matrix multiplication has different rules and different properties. We have explained every concept of multiplication matrices. So, go through the entire article to understand how to do multiplication of matrices. Also, you will get to know what is the rules to do multiplication by reading this article.
