All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 9 Estimate Sums and Differences will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 9 Estimate Sums and Differences
Math in My World
Example 1
Lucita and Alexis went scuba diving for 7\(\frac{1}{3}\) hours. The next day, they went scuba diving for 4\(\frac{2}{3}\) hours. About how many hours did they spend scuba diving altogether?
Estimate 7\(\frac{1}{3}\) + 4\(\frac{2}{3}\).
Round each mixed number to the nearest whole number.

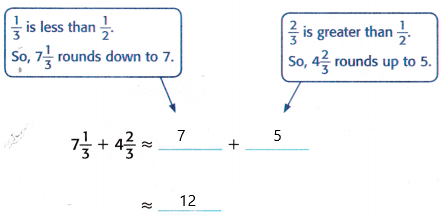
So, 7\(\frac{1}{3}\) + 4\(\frac{2}{3}\) ≈ 12.
Lucita arid Alexis spent about 12 hours scuba diving altogether.
Helpful Hint
The ≈ means about or approximately equal to.
Example 2
One sea anemone is 3\(\frac{1}{4}\) feet across while a second sea anemone is 5\(\frac{3}{4}\) feet across. About how much longer across is the second anemone?
Estimate 5\(\frac{3}{4}\) – 3\(\frac{1}{4}\).
Round each mixed number to the nearest whole number.
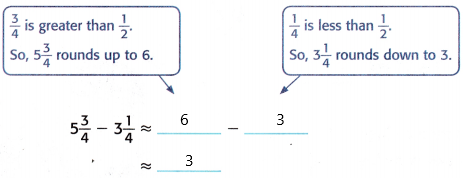
So, 5\(\frac{3}{4}\) – 3\(\frac{1}{4}\) ≈ 3
The second sea anemone is about 3 the first sea anemone.
Guided Practice
Estimate by rounding each mixed number to the nearest whole number.
Question 1.
2\(\frac{1}{8}\) + 3\(\frac{5}{8}\)
Answer:
The above-given:
2 1/8 + 3 5/8
1/8 is less than 1/2, so 1/8 rounds up to 0.
2 + 0 = 2
5/8 rounds up to 1.
3 + 1 = 4
Now add: 2 + 4 = 6
Therefore, 2\(\frac{1}{8}\) + 3\(\frac{5}{8}\) = 6
Talk Math
Explain how you would estimate 8\(\frac{4}{7}\) – 4\(\frac{2}{7}\).
Answer:
The above-given:
8 4/7 – 4 2/7
Explanation:
– Take the given fraction.
– Convert the given fraction into decimals by dividing the numerator by the denominator.
– If the obtained number to the right of the decimal point is 0.5 or more, then add 1 to the left of the decimal point and remove the decimal part.
– If the obtained number to the right of the decimal point is lesser than 0.5, then leave the number to the left of the decimal point and remove the decimal part.
– Write the new number as a rounded number.
4/7 = 0.6; so it can be rounded up to 1.
8 + 1 = 9
2/7 = 0.3
The number right of the decimal point is .3 which is lesser than .5. So, add 0 to the left of the decimal point and remove the decimal part.
4 + 0 = 4
Now subtract: 9 – 4 = 5
Therefore, 8\(\frac{4}{7}\) – 4\(\frac{2}{7}\) = 5.
Question 2.
5\(\frac{2}{9}\) – 3\(\frac{2}{3}\)
Answer:
The above-given:
5 2/9 – 3 2/3
– Take the given fraction.
– Convert the given fraction into decimals by dividing the numerator by the denominator.
– If the obtained number to the right of the decimal point is 0.5 or more, then add 1 to the left of the decimal point and remove the decimal part.
– If the obtained number to the right of the decimal point is lesser than 0.5, then leave the number to the left of the decimal point and remove the decimal part.
– Write the new number as a rounded number.
The actual value of 2/9 = 0.2222
The round-off value is 0 because .2 is less than the .5
5 2/9 = 5 + 0 = 5
Now take another mixed fraction and convert it to the whole number.
3 2/3:
The actual value of 2/3 is 0.66666
The round-off value is 1 because .6 is greater than .5 so we have to add 1 as per the above rules.
3 + 1 = 4
Now subtract 5 – 4 = 1
Therefore, 5\(\frac{2}{9}\) – 3\(\frac{2}{3}\) = 1.
Question 3.
3\(\frac{3}{5}\) + 1\(\frac{1}{5}\)
Answer:
The above-given:
3 3/5 + 1 1/5
Take the first fraction and round off:
3 3/5:
3/5 can be written as 1 because the actual value of the 3/5 is 0.6
.6 is greater than .5 so we have to add 1.
3 + 1 = 4
Take another fraction:
1 1/5:
1/5 can be written as 0 because the actual value of 1/5 is 0.2
.2 is less than .5 so leave the number to the left of the decimal point and remove the decimal part.
1 + 0 =1
Now add: 4 + 1 = 5
Therefore, 3\(\frac{3}{5}\) + 1\(\frac{1}{5}\) = 5
Independent Practice
Estimate by rounding each mixed number to the nearest whole number.
Question 4.
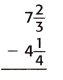
Answer:
The above-given:
7 2/3 – 4 1/4
Take the first fraction and round off to the nearest whole number:
7 2/3:
2/3 can be written as 1.
The actual value of 2/3 is 0.66666
.6 is greater than .5 so we have to add 1 as per the above rules.
7 + 1 = 8
Take the second fraction:
4 1/4:
1/4 can be rounded to 0 because its actual value is 0.25
.25 is less than .5 so leave the number to the left of the decimal point and remove the decimal part.
4 + 0 = 4
Now subtract: 8 – 4 = 4
Therefore, 7 2/3 – 4 1/4 = 4
Question 5.
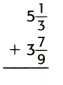
Answer:
The above-given:
5 1/3 + 3 7/9
Take the first fraction and round off to the nearest whole number:
5 1/3:
1/3 can be rounded to 0. Because its actual number is 0.33333
.3 is less than .5 so leave the number to the left of the decimal point and remove the decimal part.
5 + 0 = 5
Take the second fraction:
3 7/9:
7/9 can be rounded up to 1 because the 7/9 actual number is 0.7777
.7 is greater than .5 so add 1.
3 + 1 = 4
Now add: 5 + 4 = 9
Therefore, 5 1/3 + 3 7/9 = 9
Question 6.
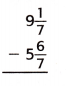
Answer:
The above-given fraction:
9 1/7 – 5 6/7
Take the first fraction and round off to the nearest whole number:
9 1/7:
1/7 can be rounded to 0 because 1/7 actual value is 0.1
.1 is less than .5 so leave the number to the left of the decimal point and remove the decimal part.
9 + 0 = 9
Take the second fraction:
5 6/7:
6/7 can be rounded to 1 because the 6/7 actual value is 0.8
.8 is greater than .5 so add 1.
5 + 1 = 6
Now 9 – 6 = 3
Therefore, 9 1/7 – 5 6/7 = 3
Question 7.
6\(\frac{7}{10}\) – 1\(\frac{1}{5}\)
Answer:
The above-given:
6 7/10 – 1 1/5
Take the first fraction and round off to the nearest whole number:
6 7/10:
7/10 can be rounded off to 1 because the actual value of 7/10 is 0.7 and moreover, .7 is greater than .5 so we have to add 1.
6 + 1 = 7
Now take another fraction:
1 1/5:
1/5 can be rounded to 0 because the actual value of 1/5 is 0.2
.2 is less than .5 so leave the number to the left of the decimal point and remove the decimal part.
1 + 0 = 1
Now subtract: 7 – 1 = 6
Therefore, 6\(\frac{7}{10}\) – 1\(\frac{1}{5}\) = 6.
Question 8.
8\(\frac{11}{12}\) + 4\(\frac{1}{3}\)
Answer:
The above-given:
8 11/12 + 4 1/3
Take the first fraction and round off to the nearest whole number:
8 11/12:
11/12 can round to 1 because the actual value of 11/12 is 0.9
.9 is greater than .5 so we have to add 1.
8 + 1 = 9
Take another fraction:
4 1/3:
1/3 can be rounded to 0 because its actual value is 0.3
.3 is less than .5 so leave the number to the left of the decimal point and remove the decimal part.
4 + 0 = 4
Now add: 9 + 4 = 13
Therefore, 8\(\frac{11}{12}\) + 4\(\frac{1}{3}\) = 13.
Question 9.
15\(\frac{3}{7}\) – 3\(\frac{4}{7}\)
Answer:
The above-given:
15 3/7 – 3 4/7
Take the first fraction and round off to the nearest whole number:
15 3/7:
3/7 can be rounded to 0 because its actual value is 0.4
.4 is less than .5 so leave the number to the left of the decimal point and remove the decimal part.
15 + 0 = 15
Now take another fraction:
3 4/7:
4/7 can be rounded to 1 because its actual value is 0.5
.5 is equal to .5 so we have to add 1.
3 + 1 = 4
Now subtract: 15 – 4 = 11
Therefore, 15\(\frac{3}{7}\) – 3\(\frac{4}{7}\) = 11.
Question 10.
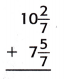
Answer:
The above-given:
10 2/7 + 5 5/7
Take the fractions and round off the value:
2/7 can be rounded to 0 because 2/7 actual value is 0.3
.3 is less than .5 so leave the number to the left of the decimal point and remove the decimal part.
10 + 0 = 10
5/7 can be rounded to 1 because its actual value is 0.7
.7 is greater than .5 so add 1.
5 + 1 = 6
Now add: 10 + 6 = 16
Therefore, 10 2/7 + 5 5/7 = 16.
Question 11.
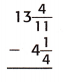
Answer:
The above-given:
13 4/11 – 4 1/4
Now round off the fractions to the nearest whole number.
4/11 can be rounded to 0 {The actual value is 0.3}
1/4 can be rounded to 0 { The actual value is 0.25}
13 + 0 = 13
4 + 0 = 4
Now subtract 13 – 4 = 9
Therefore, 13 4/11 – 4 1/4 = 9
Question 12.
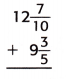
Answer:
The above-given:
12 7/10 + 9 3/5
Now round off the fractions to the nearest whole number.
7/10 can be round to 1 { The actual value of 7/10 is 0.7}
3/5 can be rounded to 1 { The actual value of 3/5 is 0.6}
12 + 1 = 13
9 + 1 = 10
Now add: 13 + 10 = 23
Therefore, 12 7/10 + 9 3/5 = 23
Question 13.
19\(\frac{3}{7}\) + \(\frac{13}{14}\)
Answer:
The above-given:
19 3/7 + 13/14
Now round off the fractions to the nearest whole number.
3/7 can be rounded to 0 { The actual value of 3/7 is 0.4}
13/14 can be rounded to 1 { The actual value of 13/14 is 0.9}
19 + 0 = 19
0 + 1 = 1
Now add: 19 + 1 = 20
Therefore, 19\(\frac{3}{7}\) + \(\frac{13}{14}\) = 20
Question 14.
7\(\frac{7}{9}\) – 1\(\frac{5}{18}\)
Answer:
The above-given:
7 7/9 – 1 5/18
Now round off the fractions to the nearest whole number.
7/9 can be rounded to 1 { The actual value of 7/9 is 0.7}
5/18 can be rounded to 0 { The actual value of 5/18 is 0.3}
7 + 1 = 8
1 + 0 = 1
Now subtract: 8 – 1 = 7
Therefore, 7\(\frac{7}{9}\) – 1\(\frac{5}{18}\) = 7
Question 15.
\(\frac{9}{16}\) + 16\(\frac{5}{8}\)
Answer:
The above-given value:
9/16 + 16 5/8
Now round off the fractions to the nearest whole number.
9/16 can be rounded to 1
5/8 can be rounded to 1.
0 +1 = 1
16 + 1 = 17
Now add: 1 + 17 = 18
Therefore, \(\frac{9}{16}\) + 16\(\frac{5}{8}\) = 18
Problem Solving
Question 16.
Liam spent 1\(\frac{3}{4}\) hours playing board games and 2\(\frac{1}{4}\) hours watching a movie. About how much time did Liam spend altogether on these two activities? Round each mixed number to the nearest whole number.
Answer:
The above-given:
The number of hours Liam spent playing games = 1 3/4
The number of hours Liam spent watching movie = 2 1/4
The total number of hours she spent on both activities = x
x = 1 3/4 + 2 1/4
Now estimate and round off the mixed fractions to the nearest whole number.
3/4 can be rounded to 1
1/4 can be rounded to 0.
1 + 1 = 2
2 + 0 = 2
Now add:
x = 2 + 2
x = 4
Therefore, Liam spent 4 hours on both activities.
Question 17.
Mathematical PRACTICE 2 Use Number Sense Beth walked 10\(\frac{7}{8}\) miles one week. She walked 2\(\frac{1}{4}\) fewer miles the following week. About how many miles did she walk
the second week? Round each mixed number to the nearest whole number.
Answer:
The above-given:
The number of miles Beth walked in one week = 10 7/8
The number of fewer miles she walked the following week = 2 1/4
The number of miles she walks = x
x = 10 7/8 – 2 1/4
Now round off the mixed fractions to the nearest whole number.
7/8 can be rounded to 1
1/4 can be rounded to 0.
10 + 1 = 11
2 + 0 = 2
Now subtract:
x = 11 – 2
x = 9
Therefore, she walked 9 miles.
Question 18.
Patrick has played guitar for 3\(\frac{5}{6}\) years. Gen has played guitar for 6\(\frac{1}{12}\) years. Estimate how many more years Gen has played guitar than Patrick. Round each mixed number to the nearest whole number.

Answer:
The above-given:
The number of years Patrick has played the guitar = 3 5/6
The number of years Gen has played the guitar = 6 1/12
The number of more years Gen has played than Patrick = x
x = 6 1/12 – 3 5/6
Now round off the mixed fractions to the nearest whole number.
1/12 can be rounded to 0
5/6 can be rounded to 1
6 + 0 = 6
3 + 1 = 4
Now subtract:
x = 6 – 4
x = 2
Therefore, Gen has played 2 years more than Patrick.
HOT Problems
Question 19.
Mathematical PRACTICE 3 Justify Conclusions Select two mixed numbers whose estimated difference is 1. Justify your selection.
Answer:
The equation can be written as:
x – y = 1
The x value would be 6 1/2
The y value would be 5 1/2
1/2 can be rounded to 1.
6 + 1 = 7
5 + 1 = 6
Now substitute and subtract:
x – y = 1
7 – 6 = 1
1 = 1
Therefore, those two mixed numbers are 6 1/2 and 5 1/2.
Question 20.
? Building on the Essential Question How does number sense of fractions help when estimating sums and differences?
Answer:
We don’t add or subtract the denominator. When you compare fractions like 1/4 and 1/8 we have to find the factors that we represent like 4 x 2 = 8. Finally, 4 and 2 is the answer.
– Estimating a fraction will give us the gist of the fraction. However, we will seldom guess the exact answer with it. If we only need a general idea of the answer, estimations are helpful.
McGraw Hill My Math Grade 5 Chapter 9 Lesson 9 My Homework Answer Key
Practice
Estimate by rounding each mixed number to the nearest whole number.
Question 1.
2\(\frac{1}{5}\) + 6\(\frac{4}{5}\)
Answer:
The above-given:
2 1/5 + 6 4/5
Now round off the mixed fractions into the nearest whole number.
1/5 can be rounded to 0
4/5 can be rounded to 1
2 + 0 = 2
6 + 1 = 7
Now add:
2 + 7 = 9
Therefore, 2\(\frac{1}{5}\) + 6\(\frac{4}{5}\) = 9
Question 2.
6\(\frac{5}{12}\) – 2\(\frac{1}{12}\)
Answer:
The above-given:
6 5/12 – 2 1/12
Now round off the mixed fractions into the nearest whole number.
5/12 can be rounded to 0
1/12 can be rounded to 0.
6 + 0 = 6
2 + 0 = 2
Now subtract: 6 – 2 = 4
Therefore, 6\(\frac{5}{12}\) – 2\(\frac{1}{12}\) = 4
Question 3.
11\(\frac{8}{9}\) + 4\(\frac{1}{3}\)
Answer:
The above-given:
11 8/9 + 4 1/3
Now round off the mixed fractions into the nearest whole number.
8/9 can be rounded to 1
1/3 can be rounded to 0.
11 + 1 = 12
4 + 0 = 4
Now add: 12 + 4 = 16
Therefore, 11\(\frac{8}{9}\) + 4\(\frac{1}{3}\) = 16
Question 4.
7\(\frac{1}{6}\) – 5\(\frac{3}{4}\)
Answer:
The above-given:
7 1/6 – 5 3/4
Now round off the mixed fractions into the nearest whole number.
1/6 can be rounded to 0
3/4 can be rounded to 1
7 + 0 = 7
5 + 1 = 6
Now subtract: 7 – 6 = 1
Therefore, 7\(\frac{1}{6}\) – 5\(\frac{3}{4}\) = 1.
Question 5.
\(\frac{11}{18}\) + 6\(\frac{1}{10}\)
Answer:
The above-given:
11/18 + 6 1/10
Now round off the mixed fractions into the nearest whole number.
11/18 can be rounded to 1
1/10 can be rounded to 0
0 + 1 = 1
6 + 0 = 6
Now add: 1 + 6 = 7
Therefore, \(\frac{11}{18}\) + 6\(\frac{1}{10}\) = 7
Question 6.
15\(\frac{1}{3}\) – 2\(\frac{5}{8}\)
Answer:
The above-given:
15 1/3 – 2 5/8
Now round off the mixed fractions into the nearest whole number.
1/3 can be rounded to 0.
5/8 can be rounded to 1.
15 + 0 = 15
2 + 1 = 3
Now subtract: 15 – 3 = 12
Therefore, 15\(\frac{1}{3}\) – 2\(\frac{5}{8}\) = 12.
Problem Solving
For Exercises 7—9, use the pictures shown.

Question 7.
About how much taller is the birdhouse than the swing set? Round each mixed number to the nearest whole number.
Answer:
The above-given pictures:
The height of the birdhouse = 14 9/16
The height of the swing set = 8 1/4
The number of feet more the birdhouse is than the swing set = x
x = 14 9/16 – 8 1/4
Now round off the mixed fractions into the nearest whole number.
9/16 can be rounded to 1.
1/4 can be rounded to 0.
14 + 1 = 15
8 + 0 = 8
Now subtract 15 – 8 = 7
Therefore, the birdhouse is 7 feet more than the swing set.
Question 8.
About how much taller is the birdhouse than the tree house? Round each mixed number to the nearest whole number.
Answer:
The above-given:
The height of the birdhouse = 14 9/16
The height of the tree house = 11 13/16
The number of feet more the birdhouse is than the tree house = x
x = 14 9/16 – 11 13/16
Now round off the mixed fractions into the nearest whole number.
13/16 can be rounded to 1.
9/16 can be rounded to 1.
14 + 1 = 15
11 + 1 = 12
Now subtract:
x = 15 – 12
x = 3
Therefore, the birdhouse is 3 feet more than the tree house.
Question 9.
Mathematical PRACTICE 1 Plan Your Solution Find the approximate height difference between the birdhouse and the tree house. Is it greater than or less than the approximate difference in height between the swing set and the tree house? Round each mixed number to the nearest whole number.
Answer:
The difference between a birdhouse and a tree house:
The height of the birdhouse = 14 9/16
The height of the tree house = 11 13/16
The difference between birdhouse and tree house = x
x = 14 9/16 – 11 13/16
Now round off the mixed fractions into the nearest whole number.
13/16 can be rounded to 1.
9/16 can be rounded to 1.
14 + 1 = 15
11 + 1 = 12
Now subtract:
x = 15 – 12
x = 3
The difference between a swing set and a tree house:
The height of the tree house = 11 13/16
The height of the swing set = 8 1/4
difference= x
x = 11 13/16 – 8 1/4
13/16 can be rounded to 1.
1/4 can be rounded to 0.
11 + 1 = 12
8 + 0 = 8
Now subtract:
x = 12 – 8
x = 4
3 < 4
Therefore, the height difference between the birdhouse and the tree house is less than the difference in height between the swing set and the tree house.
Test Practice
Question 10.
Use the table at the right About how many hours did Frank ride his bike altogether?
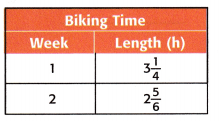
A. 4 hours
B. 5 hours
C. 6 hours
D. 7 hours
Answer: Option C is the correct answer.
Explanation:
The above-given:
The number of hours Frank rides his bike in the first week = 3 1/4
The number of hours Frank rides his bike in the second week = 2 5/6
The total number of hours altogether = x
x = 3 1/4 + 2 5/6
Now round off the mixed fractions into the nearest whole number.
1/4 can be rounded to 0.
5/6 can be rounded to 1.
3 + 0 = 3
2 + 1 = 3
x = 3 + 3
x = 6
Therefore, he rides 6 hours.