All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 7 Subtract Unlike Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 7 Subtract Unlike Fractions
Math in My World
Example 1
A female Cuban tree frog can be up to \(\frac{5}{12}\) foot long. A male Cuban tree frog can be up to \(\frac{1}{4}\) foot long. How much longer is the female Cuban tree frog than the male?
Find \(\frac{5}{12}\) – \(\frac{1}{4}\).
Write equivalent, like fractions using the least common denominator, LCD. The LCD of \(\frac{5}{12}\) and \(\frac{1}{4}\) is 12.
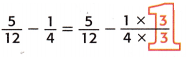
Write equivalent fractions using LCD
= \(\frac{5}{12}\) – \(\frac{3}{12}\)
Multiply.
= \(\frac{5-3}{12}\) or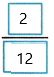 
Subtract like fractions.
= 
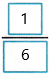
Simplify.
A female Cuban tree frog is foot longer than the male.
Check for Reasonableness Use benchmark fractions to check.
Since, \(\frac{1}{6}\) < \(\frac{1}{2}\), your answer is reasonable.
Example 2
Jessie finished \(\frac{1}{2}\) of her homework. Lakshani finished \(\frac{4}{5}\) of her homework. What fraction more of her homework did Lakshani finish than Jessie?
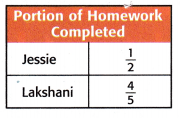
Estimate Use benchmark fractions.
\(\frac{4}{5}\) – \(\frac{1}{2}\) ≈ 1 – \(\frac{1}{2}\) = 
Subtract \(\frac{4}{5}\) – \(\frac{1}{2}\).
Write equivalent, like fractions using the least common denominator, LCD. The LCD of \(\frac{4}{5}\) and \(\frac{1}{2}\) is 1o.
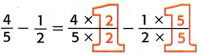
Write equivalent fractions using the LCD.
= \(\frac{8}{10}\) – \(\frac{5}{10}\) Multiply.
= \(\frac{8-5}{10}\), or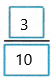 
Subtract like fractions.
Lakhani finished more of her homework than Jessie.
Talk Math
Describe the steps you can use to find \(\frac{3}{4}\) – \(\frac{1}{12}\).
Answer:
The above-given unlike fractions:
3/4 – 1/12
step 1: Find the common denominator
12 is the least common multiple of denominators 4 and 12. Use it to convert to equivalent fractions with this common denominator.
= 3 x 3/4 x 3 – 1 x 1/12 x 1
= 9/12 – 1/12
Step 2: Now the denominators are equal so subtract.
= (9 – 1)/12
= 8/12
Here we can simplify 8/12 by reducing the fractions to the lowest terms.
4 is the greatest common divisor of 8 and 12. Reduce by dividing both the numerator and denominator by 4.
= 8 ÷ 4/12 ÷ 4
= 2/3
Guided Practice
Question 1.
Subtract. Write in simplest form.
\(\frac{3}{8}\) – \(\frac{1}{4}\) = 
Answer:
The above-given unlike fractions:
3/8 – 1/4
Step 1: Find a common denominator
8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
= 3 x 1/8 x 1 – 1 x 2/4 x 2
= 3/8 – 2/8
Step 2: Now the denominators are equal so subtract.
= (3 – 2)/8
= 1/8
Therefore, 3/8 – 1/4 = 
Independent Practice
Subtract. Write each in simplest form.
Question 2.
\(\frac{5}{6}\) – \(\frac{1}{2}\) = ____
Answer:
The above-given unlike fraction:
5/6 – 1/2
Step 1: Find a common denominator
6 is the least common multiple of denominators 6 and 2. Use it to convert to equivalent fractions with this common denominator.
= 5 x 1/6 x 1 – 1 x 3/2 x 3
= 5/6 – 3/6
Step 2: Here the denominators are equal so subtract directly.
= (5 – 3)/6
= 2/6
Here we can simplify further by reducing the fractions to the lowest terms.
2 is the greatest common divisor of 2 and 6. Reduce by dividing both the numerator and denominator by 2.
= 2 ÷ 2/6 ÷ 2
= 1/3
Therefore, \(\frac{5}{6}\) – \(\frac{1}{2}\) = 1/3.
Question 3.
\(\frac{2}{5}\) – \(\frac{1}{4}\) = ____
Answer:
The above-given unlike fraction:
2/5 – 1/4
Step 1: Find a common denominator
20 is the least common multiple of denominators 5 and 4. Use it to convert to equivalent fractions with this common denominator.
= 2 x 4/5 x 4 – 1 x 5/4 x 5
= 8/20 – 5/20
Step 2: Now the denominators are equal so subtract directly.
= (8 – 5)/20
= 3/20
Therefore, \(\frac{2}{5}\) – \(\frac{1}{4}\) = 3/20
Question 4.
\(\frac{4}{5}\) – \(\frac{1}{6}\) = ____
Answer:
The above-given unlike fraction:
4/5 – 1/6
Step 1: Find a common denominator
30 is the least common multiple of denominators 5 and 6. Use it to convert to equivalent fractions with this common denominator.
= 4 x 6/5 x 6 – 1 x 5/6 x 5
= 24/30 – 5/30
Step 2: Now the denominators are equal so subtract directly.
= (24 – 5)/30
= 19/30
Therefore, \(\frac{4}{5}\) – \(\frac{1}{6}\) = 19/30
Question 5.
\(\frac{7}{8}\) – \(\frac{1}{2}\) = ____
Answer:
The above-given unlike fraction:
7/8 – 1/2
Step 1: Find a common denominator
8 is the least common multiple of denominators 8 and 2. Use it to convert to equivalent fractions with this common denominator.
= 7 x 1/8 x 1 – 1 x 4/2 x 4
= 7/8 – 4/8
Step 2: Here the denominators are equal so subtract directly.
= (7 – 4)/8
= 3/8
Therefore, \(\frac{7}{8}\) – \(\frac{1}{2}\) = 3/8
Question 6.
\(\frac{7}{12}\) – \(\frac{1}{3}\) = ____
Answer:
The above-given unlike fraction:
7/12 – 1/3
Step 1: Find a common denominator
12 is the least common multiple of denominators 12 and 3. Use it to convert to equivalent fractions with this common denominator.
= 7 x 1/12 x 1 – 1 x 4/3 x 4
= 7/12 – 4/12
Step 2: Here the denominators are equal so subtract directly.
= (7 – 4)/12
= 3/12
Here we can simplify further by reducing the fractions to the lowest terms.
3 is the greatest common divisor of 3 and 12. Reduce by dividing both the numerator and denominator by 2.
= 3 ÷ 3/12 ÷ 3
= 1/4
Therefore, \(\frac{7}{12}\) – \(\frac{1}{3}\) = 1/4
Question 7.
\(\frac{5}{6}\) – \(\frac{1}{3}\) = ____
Answer:
The above-given unlike fraction:
5/6 – 1/3
Step 1: Find a common denominator
6 is the least common multiple of denominators 6 and 3. Use it to convert to equivalent fractions with this common denominator.
= 5 x 1/6 x 1 – 1 x 2/3 x 2
= 5/6 – 2/6
Step 2: Here the denominators are equal so subtract directly.
= (5 – 2)/6
= 3/6
Here we can simplify further by reducing the fractions to the lowest terms.
3 is the greatest common divisor of 3 and 6. Reduce by dividing both the numerator and denominator by 2.
= 3 ÷ 3/6 ÷ 3
= 1/2
Therefore, \(\frac{5}{6}\) – \(\frac{1}{3}\) = 1/2
Question 8.
\(\frac{2}{3}\) – \(\frac{3}{10}\) = ____
Answer:
The above-given unlike fraction:
2/3 – 3/10
Step 1: Find a common denominator
30 is the least common multiple of denominators 3 and 10. Use it to convert to equivalent fractions with this common denominator.
= 2 x 10/3 x 10 – 3 x 3/10 x 3
= 20/30 – 9/30
Step 2: Here the denominators are equal so subtract directly.
= (20 – 9)/30
= 11/30
Therefore, \(\frac{2}{3}\) – \(\frac{3}{10}\) = 11/30
Question 9.
\(\frac{5}{8}\) – \(\frac{1}{2}\) = ____
Answer:
The above-given unlike fraction:
5/8 – 1/2
Step 1: Find a common denominator
8 is the least common multiple of denominators 8 and 2. Use it to convert to equivalent fractions with this common denominator.
= 5 x 1/8 x 1 – 1 x 4/2 x 4
= 5/8 – 4/8
Step 2: Here the denominators are equal so subtract directly.
= (5 – 4)/8
= 1/8
Therefore, \(\frac{5}{8}\) – \(\frac{1}{2}\) = 1/8
Question 10.
\(\frac{4}{5}\) – \(\frac{2}{15}\) = ____
Answer:
The above-given unlike fraction:
4/5 – 2/15
Step 1: Find a common denominator
15 is the least common multiple of denominators 5 and 15. Use it to convert to equivalent fractions with this common denominator.
= 4 x 3/5 x 3 – 2 x 1/15 x 1
= 12/15 – 2/15
Step 2: Here the denominators are equal so subtract directly.
= (12 – 2)/15
= 10/15
Here we can simplify further by reducing the fractions to the lowest terms.
5 is the greatest common divisor of 10 and 15. Reduce by dividing both the numerator and denominator by 2.
= 10 ÷ 5/15 ÷ 5
= 2/3
Therefore, \(\frac{4}{5}\) – \(\frac{2}{15}\) = 2/3
Algebra Find the unknown.
Question 11.
\(\frac{5}{6}\) – \(\frac{3}{4}\) = m
m = ____
Answer:
The above-given:
5/6 – 3/4 = m
we need to find out the value of m.
Step 1: Find a common denominator
12 is the least common multiple of denominators 6 and 4. Use it to convert to equivalent fractions with this common denominator.
m = 5 x 2/6 x 2 – 3 x 3/4 x 3
m = 10/12 – 9/12
Step 2: Here the denominators are equal so subtract directly.
m = (10 – 9)/12
m = 1/12
Question 12.
\(\frac{2}{3}\) – \(\frac{3}{5}\) = \(\frac{n}{15}\)
n = ____
Answer:
The above-given unlike fraction:
2/3 – 3/5 = n/15
we need to find out the value of n.
Step 1: Find a common denominator
15 is the least common multiple of denominators 3 and 5. Use it to convert to equivalent fractions with this common denominator.
= 2 x 5/3 x 5 – 3 x 3/5 x 3
= 10/15 – 9/15
Step 2: Here the denominators are equal so subtract directly.
= (10 – 9)/15
= 1/15
Therefore, the value of n is 1.
The denominator is given we found the numerator that is the value of n.
1/15 = 1 is the numerator; 15 is the denominator.
Question 13.
\(\frac{5}{12}\) – \(\frac{1}{6}\) = p
p = ____
Answer:
The above-given unlike fraction:
5/12 – 1/6 = p
we need to find out the value of p.
Step 1: Find a common denominator
12 is the least common multiple of denominators 12 and 6. Use it to convert to equivalent fractions with this common denominator.
p = 5 x 1/12 x 1 – 1 x 2/6 x 2
p = 5/12 – 2/12
Step 2: Here the denominators are equal so subtract directly.
p = (5 – 2)/12
p = 3/12
Here we can simplify further by reducing the fractions to the lowest terms.
3 is the greatest common divisor of 3 and 12. Reduce by dividing both the numerator and denominator by 2.
= 3 ÷ 3/12 ÷ 3
= 1/4
Therefore, the value of p is 1/4.
Problem Solving
Question 14.
Angie rides her bicycle \(\frac{2}{3}\) mile to school. On Friday, she took a shortcut so that the ride to school was \(\frac{1}{9}\)– mile shorter. How long was Angie’s bicycle ride on Friday?
Answer:
The above-given:
The number of miles Angie rides her bicycle to school = 2/3
The number of miles she rides on Friday = 1/9
The number of miles Angie bicycle rode on Friday = x
x = 2/3 – 1/9
Step 1: Find a common denominator
9 is the least common multiple of denominators 3 and 9. Use it to convert to equivalent fractions with this common denominator.
x = 2 x 3/3 x 3 – 1 x 1/9 x 1
x = 6/9 – 1/9
Step 2: Here the denominators are equal so subtract directly.
x = (6 – 1)/9
x = 5/9
Therefore, she rides 5/9 miles on Friday.
Question 15.
Mathematical PRACTICE 6 Be Precise ollie used \(\frac{1}{2}\) cup of vegetable oil to make brownies. She used another \(\frac{1}{3}\) cup of oil to make muffins. How much more oil did she use to make brownies?
Answer:
The above-given:
The number of cups of oil used by Ollie to make brownies = 1/2
The number of cups of oil used by Ollie to make muffins = 1/3
The number of more oil she used to make brownies = b
b = 1/2 – 1/3
Step 1: Find a common denominator
6 is the least common multiple of denominators 2 and 3. Use it to convert to equivalent fractions with this common denominator.
b = 1 x 3/2 x 3 – 1 x 2/3 x 2
b = 3/6 – 2/6
Step 2: Here the denominators are equal so subtract directly.
b = (3 – 2)/6
b = 1/6
Therefore, 1/6 more oil is used to make brownies.
Question 16.
Danielle poured \(\frac{3}{4}\) gallon of water from a \(\frac{7}{8}\)-gallon bucket How much water is left in the bucket?
Answer:
The above-given:
The number of gallons of water Danielle poured = 3/4
The number of gallons of water in a bucket = 7/8
The number of gallons of water left in the bucket = b
b = 7/8 – 3/4
Step 1: Find a common denominator
8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
b = 7 x 1/8 x 1 – 3 x 2/4 x 2
b = 7/8 – 6/8
Step 2: Here the denominators are equal so subtract directly.
b = (7 – 6)/8
b = 1/8
Therefore, 1/8 gallons of water left in the bucket.
HOT Problems
Question 17.
Mathematical PRACTICE 2 Use Number Sense Is finding \(\frac{9}{10}\) – \(\frac{1}{2}\) the same as finding \(\frac{9}{10}\) – \(\frac{1}{4}\) – \(\frac{1}{4}\) ? Explain.
Answer:
The above-given:
9/10 – 1/2 = 9/10 – 1/4 – 1/4
9/10 – 1/2 = 9/10 – 2/4
we need to find out whether both equations will get the same answer or not
9/10 – 1/2
Step 1: Find a common denominator
10 is the least common multiple of denominators 10 and 2. Use it to convert to equivalent fractions with this common denominator.
= 9 x 1/10 x 1 – 1 x 5/2 x 5
= 9/10 – 5/10
= (9 – 5)/10
= 4/10
= 2/5
Now check out the answer for 9/10 – 2/4
Step 1: Find a common denominator
20 is the least common multiple of denominators 10 and 4. Use it to convert to equivalent fractions with this common denominator.
= 9 x 2/10 x 2 – 2 x 5/4 x 5
= 18/20 – 10/20
= 8/20
= 2/5
Therefore, both are have the same answer.
Question 18.
? Building on the Essential Question How are equivalent fractions used when subtracting, unlike fractions?
Answer:
Equivalent fractions are used when adding and subtracting fractions. In order to add or subtract a fraction, the fractions involved must be like fractions. If they are unlike fractions, then the unlike fractions must be converted into equivalent fractions that share the same denominator in order to be added or subtracted.
McGraw Hill My Math Grade 5 Chapter 9 Lesson 7 My Homework Answer Key
Practice
Subtract. Write each in simplest form.
Question 1.
\(\frac{1}{2}\) – \(\frac{1}{4}\) = ____
Answer:
The above-given unlike fraction:
1/2 – 1/4
Step 1: Find a common denominator
4 is the least common multiple of denominators 2 and 4. Use it to convert to equivalent fractions with this common denominator.
= 1 x 2/2 x 2 – 1 x 1/4 x 1
= 2/4 – 1/4
Step 2: Here the denominators are equal so subtract directly.
= (2 – 1)/4
= 1/4
Therefore, \(\frac{1}{2}\) – \(\frac{1}{4}\) = 1/4.
Question 2.
\(\frac{7}{8}\) – \(\frac{1}{4}\) = ____
Answer:
The above-given unlike fraction:
7/8 – 1/4
Step 1: Find a common denominator
8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
= 7 x 1/8 x 1 – 1 x 2/4 x 2
= 7/8 – 2/8
Step 2: Here the denominators are equal so subtract directly.
= (7 – 2)/8
= 5/8
Therefore, \(\frac{7}{8}\) – \(\frac{1}{4}\) = 5/8
Question 3.
\(\frac{7}{12}\) – \(\frac{1}{6}\) = ____
Answer:
The above-given unlike fraction:
7/12 – 1/6
Step 1: Find a common denominator
12 is the least common multiple of denominators 12 and 6. Use it to convert to equivalent fractions with this common denominator.
= 7 x 1/12 x 1 – 1 x 2/6 x 2
= 7/12 – 2/12
Step 2: Here the denominators are equal so subtract directly.
= (7 – 2)/12
= 5/12
Therefore, \(\frac{7}{12}\) – \(\frac{1}{6}\) = 5/12
Problem Solving
Question 4.
The average rainfall in April and October for Springfield is shown in the table below. How much more rain falls on average in April than in October?
Answer:
The above-given:
The number of inches an average rainfall in April = 11/16
The number of inches an average rainfall in October = 3/8
The number of inches of more rainfall on average in April than in October = a
a = 11/16 – 3/8
Step 1: Find a common denominator
16 is the least common multiple of denominators 16 and 8. Use it to convert to equivalent fractions with this common denominator.
= 11 x 1/16 x 1 – 3 x 2/8 x 2
= 11/16 – 6/16
= (11 – 6)/16
= 5/16
Therefore, 5/16 inches more rainfall in April than in October.
Question 5.
Trisha helped clean up her neighbourhood by picking up plastic. She collected \(\frac{3}{4}\) pound of plastic the first day and \(\frac{1}{6}\) pound of plastic the second day. How much more trash did she collect the first day than the second day?
Answer:
The above-given:
The number of pounds of plastic collected on the first day by Trisha = 3/4
The number of pounds of plastic collected on the second day by Trisha =1/6
The number of pounds of trash collected on the first day than the second = f
f = 3/4 – 1/6
Step 1: Find a common denominator
12 is the least common multiple of denominators 4 and 6. Use it to convert to equivalent fractions with this common denominator.
= 3 x 3/4 x 3 – 1 x 2/6 x 2
= 9/12 – 2/12
= (9 – 2)/12
= 7/12
Therefore, 7/12 pounds more trash was collected on the first day.
Question 6.
Wyatt is hiking a trail that is \(\frac{11}{12}\) mile long. After hiking \(\frac{1}{4}\) mile, he stops for water. How much farther must he hike to finish the trail?
Answer:
The above-given:
The number of miles Wyatt is hiking = 11/12
The number of miles after he stopped for water = 1/4
The number of miles there to finish the trail = x
x = 11/12 – 1/4
Step 1: Find a common denominator
12 is the least common multiple of denominators 12 and 4. Use it to convert to equivalent fractions with this common denominator.
x = 11 x 1/12 x 1 – 1 x 3/4 x 3
x = 11/12 – 3/12
x = 8/12
x = 2/3
Therefore, 2/3 miles are there to finish the trail.
Test Practice
Question 7.
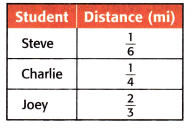
The table shows the distance each student ran on Wednesday. How much farther did Joey run than Steve?
A. \(\frac{1}{12}\) mile
B. \(\frac{5}{12}\) mile
C. \(\frac{1}{2}\) mile
D. \(\frac{5}{6}\) mile
Answer: Option C is the correct answer.
Explanation:
The above-given;
The number of miles Steve runs on Wednesday = 1/6
The number of miles Charlie ran on Wednesday = 1/4
The number of miles Joey ran on Wednesday = 2/3
The number of miles Joey ran than Steve = x
x = 2/3 – 1/6
Step 1: Find a common denominator
6 is the least common multiple of denominators 3 and 6. Use it to convert to equivalent fractions with this common denominator.
x = 2 x 2/3 x 2 – 1 x 1/6 x 1
x = 4/6 – 1/6
x = 3/6
x = 1/2
Therefore, 1/2 mile more Joey ran than steve.