McGraw Hill My Math Grade 5 Chapter 9 Lesson 4 Answer Key Use Models to Add Unlike Fractions

All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 4 Use Models to Add Unlike Fractions will give you a clear idea of the concepts.

McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 4 Use Models to Add Unlike Fractions

Build It

To finish building a birdhouse, Jordan uses two boards. One is \(\frac{1}{2}\) foot long and the other is \(\frac{1}{4}\) foot long. What is the total length of the boards?

1. Model each fraction using fraction tiles and place them side by side

2. Find fraction tiles that will match the length of the combined tiles. Line them up below the model
3. Count There are ____ of the \(\frac{1}{4}\)-fraction tiles in all. This represents the fraction \(\frac{3}{4}\).
So, \(\frac{1}{2}\) + \(\frac{1}{4}\) = . The total length of the boards is foot.
Answer:
The number of tiles is 3.
1/2 + 1/4
1/2 = 1/4 + 1/4
Now add:
1/4 + 1/4 + 1/4 = 3/4
Therefore, 1/2 + 1/4 = . The total length of the boards is foot.

Try It

Mama’s family ate \(\frac{2}{3}\) of a strawberry pie and Brendan’s family ate \(\frac{3}{4}\) of a different strawberry pie. How much did they eat altogether?

1. Model each fraction using fraction tiles and place them side by side.

2. Find fraction tiles that will match the length of the combined tiles. Line them up below the model.
3. Count. There are ____ of the \(\frac{1}{12}\)-fraction tiles in all. This represents the fraction \(\frac{17}{12}\), or 1\(\frac{5}{12}\).
Answer:
4/12 = 1/3
so we can say that,
1/3 = 1/12 + 1/12 + 1/12 + 1/12
3/12 = 1/4
so we can say that,
1/4 = 1/12 + 1/12 + 1/12
Therefore, the number of tiles is 17.
now add:
= 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12.
= 17/12
In mixed numbers, we can write 1 5/12.

Helpful Hint
Follow these steps to write \(\frac{17}{12}\) as a mixed number.
\(\frac{17}{12}\) = \(\frac{12}{12}\) + \(\frac{5}{12}\)
= 1\(\frac{5}{12}\)
They ate 1\(\frac{5}{12}\) strawberry pies altogether.

Talk About It

Question 1.
In the first activity, how does the denominator of the sum, \(\frac{3}{4}\) compare to the denominators of the addends, \(\frac{1}{2}\) and \(\frac{1}{4}\) ?
Answer:
The denominator of the sum is the least common multiple of the denominators of the addends.

Question 2.
In the second activity, how does the denominator of the sum, 1\(\frac{5}{12}\), compare to the denominators of the addends, \(\frac{2}{3}\) and \(\frac{3}{4}\) ?
Answer:
The denominator of the sum is the least common multiple of the denominators of the addends

Question 3.
Mathematical PRACTICE 6 Explain to a Friend Use your answers from Exercises 1 and 2 to predict the denominator of the sum of \(\frac{1}{3}\) and \(\frac{1}{4}\). Explain.
Answer:
The denominator of the sum will be 12, it is the least common multiple of 3 and 4.
1/3 + 1/4
The lcm is 12.
4 + 3/12 = 7/12.

Practice It

Find the sum using fraction tiles. Write in simplest form. Draw the models.

Question 4.
\(\frac{2}{3}\) + \(\frac{1}{6}\) = _____
Answer:
The above-given unlike fractions:
2/3 + 1/6
2/3 = 1/3 + 1/3

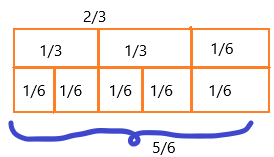
1/3 = 1/6 + 1/6 = 2/6
if we simplify 2/6, then we get 1/3 so we wrote 1/3 = 1/6 + 1/6
The number of tiles is 5.
Now add:
1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 5/6
Therefore, 2/3 + 1/6 = 5/6
Or else, we can take LCM
The LCM of 3 and 6 are 6
4 + 1/6 = 5/6.

Question 5.
\(\frac{3}{8}\) + \(\frac{1}{4}\) = _____
Answer:
The above-given unlike fractions:
3/8 + 1/4
3/8 = 1/8 + 1/8 + 1/8
1/4 = 1/8 + 1/8
If we add 1/8 + 1/8 then we get 2/8.
if we simplify 2/8, then we get 1/4 because 2 x 4 = 8. (divide with 2).
Fraction tiles:

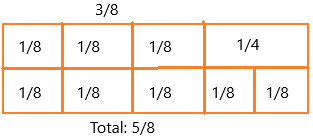
The number of tiles = 5
If we add: 1/8 + 1/8 + 1/8 + 1/8 + 1/8
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
= ( 1 + 1+ 1+ 1+ 1)/8
= 5/8
Therefore, 3/8 + 1/4 = 5/8.

Question 6.
\(\frac{3}{10}\) + \(\frac{1}{5}\) = _____
Answer:
The above-given unlike fractions:
3/10 + 1/5
Firstly, making the like fractions means making the denominator the same.
3/10 = 1/10 + 1/10 + 1/10
1/5 = 1/10 + 1/10
if we add 1/10 + 1/10 then we get 2/10
if we simplify 2/10, then we get 1/5 which means we divide 2/10 by 5  (2 x 5 = 10).

The number of tiles = 5
if we add: 1/10 + 1/10 + 1/10 + 1/10 + 1/10
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
= ( 1 + 1+ 1+ 1+ 1)/10
= 5/10
Therefore, 3/10 + 1/5 = 5/10 = 1/2

Question 7.
\(\frac{5}{8}\) + \(\frac{1}{4}\) = _____
Answer:
The above-given unlike fractions:
5/8 + 1/4
Firstly, making the like fractions means making the denominator the same.
we can write 5/8 as 1/8 + 1/8 + 1/8 + 1/8 + 1/8
we can write 1/4 as 1/8 + 1/8
if we add 1/8 + 1/8 = 2/8, then we get 1/4. ( 2 x 4 = 8)

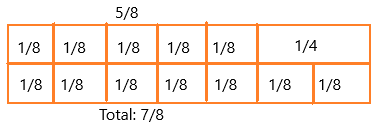
The number of tiles = 7
if we add: 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
= ( 1 + 1+ 1+ 1+ 1 + 1 + 1)/8
= 7/8
Therefore, 5/8 + 1/4 = 7/8.

Question 8.
\(\frac{1}{3}\) + \(\frac{1}{4}\) = _____
Answer:
The above-given unlike fractions:
1/3 + 1/4
Firstly, making the like fractions means making the denominator the same.
1/3 = 1/12 + 1/12 + 1/12 + 1/12 = 4/12
1/4 = 1/12 + 1/12 + 1/12 = 3/12
fraction tiles:

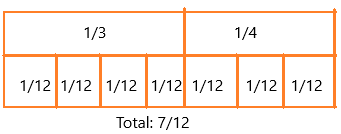
The number of tiles = 7
if we add: 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
= ( 1 + 1+ 1+ 1+ 1 + 1 + 1)/12
= 7/12
Therefore, 1/4 + 1/3 = 7/12.

Question 9.
\(\frac{3}{4}\) + \(\frac{1}{6}\) = _____
Answer:
The above-given unlike fractions:
3/4 + 1/6
Firstly, making the like fractions means making the denominator the same.
3/4 = 1/4 + 1/4 + 1/4
we can write 1/4 as 1/12 + 1/12 + 1/12 = 3/12
again 1/12 as 1/6 + 1/6 = 2/12
1/6 = 1/6

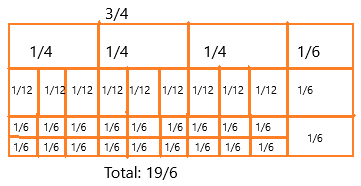
The number of tiles = 19
if we add: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 +1/6 + 1/6 + 1/6  + 1/6
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
= ( 1 + 1+ 1+ 1+ 1 + 1 + 1+ 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 +1 + 1+ 1+ 1)/6
= 19/6
Therefore, 3/4 + 1/6 = 19/6

Apply It

Mathematical PRACTICE 5 Use Math Tools Draw models to solve Exercises 10-12.

Question 10.
Alana walks east \(\frac{4}{9}\) mile to school every morning. On Saturday, she walked to a friend’s house, which is \(\frac{1}{3}\) a mile farther east from her school. How far did Alana walk to her friend’s house on Saturday?
Answer:
The above-given:
The number of miles Alana walks every morning = 4/9
The number of miles she walked to a friend’s house = 1/3
The total number of miles = x
x = 4/9 + 1/3
Now make the denominators equal.
4/9 = 1/9 + 1/9 + 1/9 + 1/9
1/3 = 1/9 + 1/9 + 1/9 = 3/9 = 1/3
model:

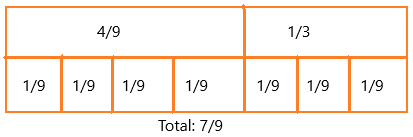
The number of tiles = 7
if we add: 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
= ( 1 + 1+ 1+ 1+ 1 + 1 + 1)/9
= 7/9
Therefore, 4/9 + 1/3 = 7/9
Therefore, the total number of miles is 7/9.

Question 11.
Mr. Hawkins gets two bonus payments every year. This year, his first bonus was \(\frac{1}{4}\) of his salary. His second bonus was \(\frac{1}{8}\) of his salary. What was the fraction of his salary for his combined bonus payments?
Answer:
The above-given:
The first bonus of his salary = 1/4
The second bonus of his salary = 1/8
The fraction of his salary for his combined bonus payments = x
x = 1/4 + 1/8
we can write 1/4 as 1/8 + 1/8
1/8 + 1/8 = 2/8 = 1/4
1/8 = 1/8
model:

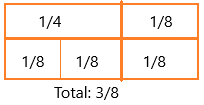
The number of tiles = 3
if we add: 1/8 + 1/8 + 1/8
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
x = ( 1 + 1+ 1)/8
x = 3/8
Therefore, 1/4 + 1/8 = 3/8
Therefore, the total bonus is 3/8.

Question 12.
At a gas station, Kurt asked for directions to the nearest town. The attendant told him to go \(\frac{5}{6}\) mile south and then \(\frac{1}{4}\) mile east. How far does Kurt have to drive to get to the town?
Answer:
The above-given:
The number of miles the attendant told him to go on south = 5/6
The number of miles the attendant told him to go on east = 1/4
The number of miles Kurt has to drive to get to the town = x
x = 5/6 + 1/4
we can write 5/6 as 1/6 + 1/6 + 1/6 + 1/6 + 1/6
1/6 = 1/12 + 1/12
1/4 = 1/12 + 1/12 + 1/12
model:

The number of tiles = 13
if we add: 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/2 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
= ( 1 + 1+ 1+ 1+ 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1)/12
= 13/12
Therefore, 5/6 + 1/4 = 13/12
Therefore, the total number of miles is 13/12

Question 13.
Mathematical PRACTICE 4 Model Math Write a real-world problem that can be solved by adding, unlike fractions.
Answer:
a sample answer is given:
Mr Hawkins gets two bonus payments every year. This year, his first bonus was \(\frac{1}{4}\) of his salary. His second bonus was \(\frac{1}{8}\) of his salary. What was the fraction of his salary for his combined bonus payments?
The first bonus of his salary = 1/4
The second bonus of his salary = 1/8
The fraction of his salary for his combined bonus payments = x
x = 1/4 + 1/8
we can write 1/4 as 1/8 + 1/8
1/8 + 1/8 = 2/8 = 1/4
1/8 = 1/8
model:

The number of tiles = 3
if we add: 1/8 + 1/8 + 1/8
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
x = ( 1 + 1+ 1)/8
x = 3/8
Therefore, 1/4 + 1/8 = 3/8
Therefore, the total bonus is 3/8.

Write About It

Question 14.
How can I use models to add fractions?
Answer:
To add fractions with unlike denominators using a visual model, you would first create models to represent each of the fractions, then find equivalent fractions with the same denominator. To do this, you have to find the least common multiple of the two fractions and then use the LCM as their common denominator.

McGraw Hill My Math Grade 5 Chapter 9 Lesson 4 My Homework Answer Key

Practice

Find the sum using the fraction tiles shown. Write in simplest form.

Question 1.
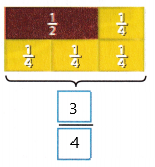
\(\frac{1}{2}\) + \(\frac{1}{4}\) = ____

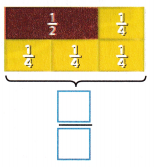
Answer:
The above-given:
1/2 + 1/4
we can write 1/2 as 1/4 + 1/4
1/4 = 1/4
Now here the denominators are equal so we can add directly.
1/4 + 1/4 + 1/4 = 3/4

Question 2.
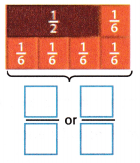
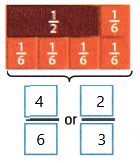
\(\frac{1}{2}\) + \(\frac{1}{6}\) = ____

Answer:
The above-given:
1/2 + 1/6
we can write 1/2 as 1/6 + 1/6 + 1/6
1/6 + 1/6 + 1/6 + 1/6 = 4/6 = 2/3

Problem Solving

Mathematical PRACTICE 5 Use Math Tools Draw models to solve Exercises 3-6. Write in simplest form.

Question 3.
After school, Maurice walks \(\frac{1}{3}\) mile to the park and then walks \(\frac{1}{2}\) mile to his house. How far does Maurice walk from school to his house?
Answer:
The above-given:
The number of miles Maurice walks to the park = 1/3
The number of miles Maurice walks to his house = 1/2
The total number of miles he walks = x
x = 1/3 + 1/2
we can write 1/3 as 1/6 + 1/6
1/2 = 1/6 + 1/6 + 1/6
model:

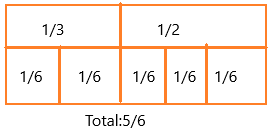
The total number of tiles = 5
if we add: 1/6 + 1/6 + 1/6 + 1/6 + 1/6
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
x = ( 1 + 1+ 1+ 1 + 1)/6
x = 5/6
Therefore, 1/3 + 1/2 = 5/6
Therefore, the total number of miles is 5/6.

Question 4.
Ricki took a survey in the fifth grade and found that \(\frac{2}{3}\) of the students ride the bus to school, and \(\frac{1}{4}\) of the students walk. What fraction of the fifth-grade students either ride the bus or walk to school?
Answer:
The above-given:
The survey taken by Ricki found that students ride the bus to school = 2/3
The survey taken by Ricki found that students by walk = 1/4
The fraction of the fifth-grade students who either ride the bus or walk to school = x
x = 2/3 + 1/4
we can write 2/3 as 1/3 + 1/3
1/3 = 1/6 + 1/6
1/6 = 1/12 + 1/12
1/4 = 1/12 + 1/12 + 1/12
model:

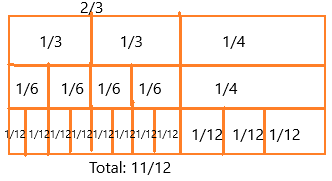
The total number of tiles = 11
if we add: 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
x = ( 1 + 1+ 1+ 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1)/12
x = 11/12
Therefore, 2/3 + 1/4 = 11/12
Therefore, the survey is on 11/12

Question 5.
Elizabeth made an English muffin pizza using \(\frac{1}{4}\) cup of cheese and \(\frac{3}{8}\) cup of sausage. How many cups of toppings did she use?
Answer:
The above-given:
The number of cups of cheese = 1/4
The number of cups of sausage = 3/8
The number of cups of toppings she uses = x
x = 1/4 + 3/8
we can write 3/8 as 1/8 + 1/8 + 1/8
we can write 1/4 as 1/8 + 1/8
model:

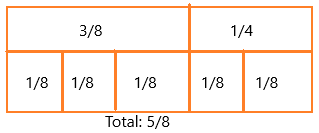
The total number of tiles = 5
if we add: 1/8 + 1/8 + 1/8 + 1/8 + 1/8
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
x = ( 1 + 1+ 1+ 1 + 1)/8
x = 5/8
Therefore, 3/8 + 1/4 = 5/8
Therefore, the total number of cups is 5/8

Question 6.
Craig and Alissa are building a sandcastle on the beach.They each have a bucket. Craig’s bucket holds \(\frac{1}{2}\) pound of sand and Alissa’s bucket holds \(\frac{9}{10}\) pound of sand. How much sand can Craig and Alissa collect together at one time?

Answer:
The above-given:
The number of pounds of sand a Craig bucket holds = 1/2
The number of pounds of sand Alissa’s bucket hold = 9/10
The total sand collected together = x
x = 1/2 + 9/10
we can write 9/10 as 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10
we can write as 1/2 as 1/10 + 1/10 + 1/10 + 1/10 + 1/10

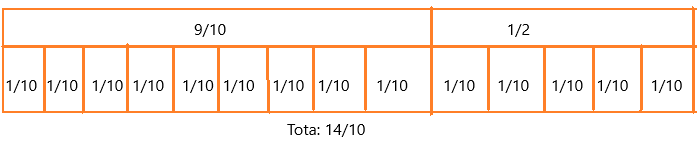
The total number of tiles = 14
Here the denominators are the same now so we can add directly the numerators and the denominator keeps the same.
x = ( 1 + 1+ 1+ 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1)/10
x = 14/10
Therefore, 9/10 + 1/2 = 14/10 = 1 2/5
Therefore, the total sand collected is 1 2/5

Vocabulary Check

Question 7.
Complete the sentence with the correct vocabulary word(s).
Fractions that have different denominators are called ______
Answer:
Fractions that have different denominators are called, unlike fractions.
These fractions are represented in groups. For example, 1/2, 1/3, 1/4, 1/5 and so on.
The above fractions are all having the different denominators.