All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 12 Subtract Mixed Numbers will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 12 Subtract Mixed Numbers
Math in My World
Example 1
One King crab weighs 2\(\frac{3}{4}\) pounds. A second King crab weighs 1\(\frac{1}{4}\)– pounds. How much more does the one King crab weigh? Use models to find the difference.
Find 2\(\frac{3}{4}\) – 1\(\frac{1}{4}\)

Estimate 3 – 1 = ____
Model 2\(\frac{3}{4}\) using fraction tiles.
Subtract 1\(\frac{1}{4}\) by crossing out 1 whole and one \(\frac{1}{4}\)-tile.
There is one whole and two \(\frac{1}{4}\)-tiles left,
which is 1\(\frac{2}{4}\), or 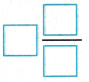

So, 2\(\frac{3}{4}\) – 1\(\frac{1}{4}\) =  .
.
The first King crab weighs  pounds more than the second.
pounds more than the second.
Check for Reasonableness ____ ≈ 
Answer:
we need to find 2 3/4 – 1 1/4
estimate: 3 – 1 = 2
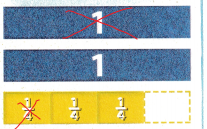
simplify the equation:
= 2 – 1 – 3/4 – 1/4
= 1 – 2/4
= 1 – 1/2
= 1 1/2.
so, 2\(\frac{3}{4}\) – 1\(\frac{1}{4}\) = 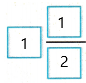
The first crab weighs,  pounds more than the second.
pounds more than the second.
check for reasonable: 2 ≈ 
Example 2
Find 6\(\frac{11}{16}\) – 2\(\frac{5}{8}\)
Estimate 7 – 3 = 4
1. Write an equivalent fraction for 2\(\frac{5}{8}\) so that the fractions have the same denominator. The LCD is 16.
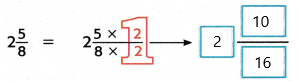
2. Subtract the wholes. Then subtract the fractions.
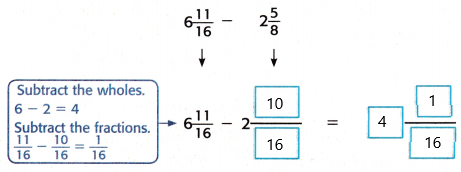
So, 6\(\frac{11}{16}\) – 2\(\frac{5}{8}\) = 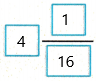
Check for Reasonableness ___4_____ ≈ 
Talk Math
Describe the steps you would take to find 3\(\frac{5}{8}\) – 2\(\frac{3}{8}\).

The above-given equation:
3 5/8 – 2 3/8
In the first step, we separate the whole numbers and the fractions.
The equation is: 3 – 2 – 5/8 – 3/8
In the second step:
simplify the equation and check whether the denominators are the same.
denominators are equal so we can subtract directly.
= 1 – 2/8
= 1 – 1/4
= 1 1/4.
Therefore, 3 5/8 – 2 3/8 = 1 1/4.
Guided Practice
Estimate, then subtract. Write each difference in simplest form.
Question 1.
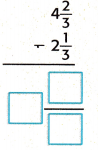
Answer:
The above-given mixed fractions:
4 2/3 – 2 1/3
Here the denominators are equal so we can subtract directly.
= 4 – 2 – 2/3 – 1/3
= 2 – 1/3
This can be written as 2 1/3.
Therefore, 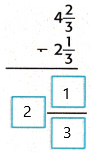
Question 2.
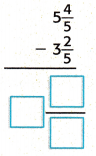
Answer:
The above-given mixed fractions:
5 4/5 – 3 2/5
= 5 – 3 – 4/5 – 2/5
= 2 – 4/5 – 2/5
Here the denominators are equal so we can subtract directly.
= 2 – 2/5
This can also be written as 2 2/5.
Therefore, 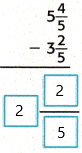
Independent Practice
Estimate, then subtract. Write each difference in simplest form.
Question 3.
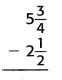
Answer:
The above-given mixed fractions:
5 3/4 – 2 1/2
= 5 – 2 – 3/4 – 1/2
= 3 – 3/4 – 1/2
Here denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 4 is the least common multiple of denominators 4 and 2. Use it to convert to equivalent fractions with this common denominator.
= 3 – (3 – 2)/4
= 3 – 1/4
This can also be written as 3 1/4
Therefore, 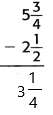
Question 4.
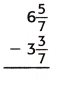
Answer:
The above-given mixed fractions:
6 5/7 – 3 3/7
Here the denominators are equal so we can subtract directly.
= 6 – 3 – 5/7 – 3/7
= 3 – 2/7
This can also be written as 3 2/7.
Therefore, 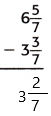
Question 5.
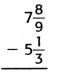
Answer:
The above-given mixed fractions:
7 8/9 – 5 1/3
= 7 – 5 – 8/9 – 1/3
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 9 is the least common multiple of denominators 9 and 3. Use it to convert to equivalent fractions with this common denominator.
= 2 – (8 – 3)/9
= 2 – 5/9
This can also be written as 2 5/9.
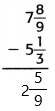
Question 6.
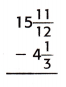
Answer:
The above-given mixed fractions:
15 11/12 – 4 1/3
= 15 – 4 – 11/12 – 1/3
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 12 is the least common multiple of denominators 12 and 3. Use it to convert to equivalent fractions with this common denominator.
= 11 – (11 – 4)/12
= 11 – 7/12
This can also be written as 11 7/12.
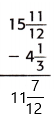
Question 7.
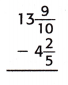
Answer:
The above-given mixed fractions:
13 9/10 – 4 2/5
= 13 – 4 – 9/10 – 2/5
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 10 is the least common multiple of denominators 10 and 5. Use it to convert to equivalent fractions with this common denominator.
= 9 – (9 – 4)/10
= 9 – 5/10
= 9 – 1/2
This can also be written as 9 1/2.
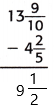
Question 8.
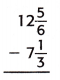
Answer:
The above-given mixed fractions:
12 5/6 – 7 1/3
= 12 – 7 – 5/6 – 1/3
= 5 – 5/6 – 1/3
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 6 is the least common multiple of denominators 6 and 3. Use it to convert to equivalent fractions with this common denominator.
= 5 – (5 – 2)/6
= 5 – 3/6
= 5 – 1/2
= 5 1/2
Therefore, 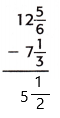
Question 9.
8\(\frac{3}{8}\) – 2\(\frac{1}{4}\) = _____
Answer:
The above-given mixed fractions:
8 3/8 – 2 1/4
= 8 – 2 – 3/8 – 1/4
= 6 – 3/8 – 1/4
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
= 6 – (3 – 2)/8
= 6 – 1/8
This can also be written as 6 1/8
Therefore, 8\(\frac{3}{8}\) – 2\(\frac{1}{4}\) = 6 1/8
Question 10.
7\(\frac{7}{8}\) – 4\(\frac{1}{2}\) = _____
Answer:
The above-given mixed fractions:
7 7/8 – 4 1/2
= 7 – 4 – 7/8 – 1/2
= 3 – 7/8 – 1/2
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 8 is the least common multiple of denominators 8 and 2. Use it to convert to equivalent fractions with this common denominator.
= 3 – (7 – 4)/8
= 3 – 2/8
= 3 – 1/4
This can also be written as 3 1/4
Therefore, 7\(\frac{7}{8}\) – 4\(\frac{1}{2}\) = 3 1/4
Question 11.
12\(\frac{7}{10}\) – 7\(\frac{2}{5}\) = _____
Answer:
The above-given mixed fractions:
12 7/10 – 7 2/5
= 12 – 7 – 7/10 – 2/5
= 5 – 7/10 – 2/5
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 10 is the least common multiple of denominators 10 and 2. Use it to convert to equivalent fractions with this common denominator.
= 5 – (7 – 4)/10
= 5 – 3/10
This can also be written as 5 3/10.
Therefore, 12\(\frac{7}{10}\) – 7\(\frac{2}{5}\) = 5 3/10.
Mathematical Practice 2 Use Algebra Find each unknown.
Question 12.
11\(\frac{11}{12}\) – 2\(\frac{1}{12}\) = x
x = _____
Answer:
The above-given mixed fractions:
11 11/12 – 2 1/12 = x
we need to find out the x value.
11 – 2 – 11/12 – 1/12
Here denominators are the same. So we can subtract directly.
x = 9 – (11 – 1)/12
x = 9 – 10/12 { in 2nd table 2 x 5 = 10; 2 x 6 = 12}
x = 9 – 5/6
This can also be written as 9 5/6
Therefore, the value of x is 9 5/6.
Question 13.
14\(\frac{9}{14}\) – 5\(\frac{2}{7}\) = c
c = _____
Answer:
The above-given mixed fractions:
14 9/14 – 5 2/7 = c
we need to find the c value.
c = 14 – 5 – 9/14 – 2/7
c = 9 – 9/14 – 2/7
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 14 is the least common multiple of denominators 14 and 7. Use it to convert to equivalent fractions with this common denominator.
c = 9 – (14 – 4)/14
c = 9 – 10/14
c = 9 – 5/7
This can also be written as 9 5/7.
Therefore, the value of c is 9 5/7.
Question 14.
18\(\frac{11}{15}\) – 9\(\frac{2}{5}\) = n
n = _____
Answer:
The above-given mixed fractions:
18 11/15 – 9 2/5 = n
we need to find the n value.
n = 18 – 9 – 11/15 – 2/5
Here the denominators are the same so we can subtract directly.
n = 9 – (11 – 2)/5
n = 9 – 9/5
This can also be written as 9 9/5.
Therefore, the value of n is 9 9/5.
Problem Solving
Question 15.
The length of Mr Cho’s garden is 8\(\frac{5}{6}\) feet. Find the width of Mr Cho’s garden if it is 3\(\frac{1}{6}\) feet less than the length.
Answer:
The above-given:
The length of the Cho’s garden in feet = 8 5/6
we need to find the width. Let it be w.
The other fraction is 3 1/6
Based on the given conditions, formulate:
8 5/6 – 3 1/6
= 8 – 3 – 5/6 – 1/6
= 5 – 5/6 – 1/6
Here denominators are the same so we can subtract directly.
w = 5 – (5 – 1)/6
w = 5 – 4/6
w = 5 – 2/3
This can also be written as 5 2/3.
Therefore, the width is 5 2/3 feet.
Question 16.
Timberly spent 3\(\frac{4}{5}\) hours and Misty spent 2\(\frac{1}{10}\) hours at gymnastics practice over the weekend. How many more hours did Timberly spend than Misty at gymnastics practice?
Answer:
The above-given:
The number of hours Timberly spent at gymnastics = 3 4/5
The number of hours Misty spent at gymnastics = 2 1/10
The number of more hours Timberly spent than Misty = g
g = 3 4/5 – 2 1/10
g = 3 – 2 – 4/5 – 1/10
g = 1 – 4/5 – 1/10
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 10 is the least common multiple of denominators 5 and 10. Use it to convert to equivalent fractions with this common denominator.
g = 1 – (8 – 1)/10
g = 1 – 7/10
This can also be written as 1 7/10
Therefore, Timberly spent 1 7/10 hours more than Misty.
Question 17.
Mathematical PRACTICE 1 Make Sense of Problems Warner lives 9\(\frac{1}{4}\)– blocks away from the ocean. Shelly lives 12\(\frac{7}{8}\) blocks away from the ocean. How many more blocks does Shelly live away from the ocean than Warner?

Answer:
The above-given:
The number of blocks away from Warner lives = 9 1/4
The number of blocks away from the ocean Shelly lives = 12 7/8
The number of blocks Shelly lives away from the ocean than Warner = o
o = 12 7/8 – 9 1/4
o = 12 – 9 – 7/8 – 1/4
o = 3 – 7/8 – 1/4
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
o = 3 – (7 – 2)/8
o = 3 – 5/8
This can also be written as 3 5/8
Therefore, she lives 3 5/8 blocks away from the ocean than a warner.
HOT Problems
Question 18.
Mathematical PRACTICE 4 Model Math Write a real-world problem involving the subtraction of two mixed numbers whose difference is less than 2\(\frac{1}{2}\). Then solve.
Answer:
The two mixed numbers are x and y
x – y < 2 1/2
a sample answer is given:
One King crab weighs 2\(\frac{3}{4}\) pounds. A second King crab weighs 1\(\frac{1}{4}\)– pounds. How much more does the one King crab weigh?
Now subtract 2 3/4 and 1 1/4
2 3/4 – 1 1/4
= 2 – 1 – 3/4 – 1/4
= 1 – 2/4
= 1 – 1/2
This can also be written as 1 1/2
1 1/2 < 2 1/2
Therefore, 2 3/4 – 1 1/4 < 2 1/2.
Question 19.
? Building on the Essential Question How can number sense help to know if I have subtracted two mixed numbers correctly?
Answer:
You could first convert each to an improper fraction. If they don’t have common denominators, then find a common denominator and use it to rewrite each fraction. Then subtract the fractions and compare the given mixed fractions. So that we can easily find out.
McGraw Hill My Math Grade 5 Chapter 9 Lesson 12 My Homework Answer Key
Practice
Estimate, then subtract. Write each difference in simplest form.
Question 1.
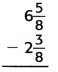
Answer:
The above-given mixed fractions:
6 5/8 – 2 3/8
= 6 – 2 – 5/8 – 3/8
Here denominators are the same so that we can subtract directly.
= 4 – (5 – 3)/8
= 4 – 2/8
= 4 – 1/4
This can also be written as 4 1/4
Therefore, 6 5/8 – 2 3/8 = 4 1/4
Question 2.
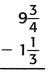
Answer:
The above- is given:
9 3/4 – 1 1/3
= 9 – 1 – 3/4 – 1/3
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 12 is the least common multiple of denominators 4 and 3. Use it to convert to equivalent fractions with this common denominator.
= 8 – (9 – 4)/12
= 8 – 5/12
This can also be written as 8 5/12.
Question 3.
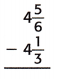
Answer:
The above-given mixed fractions:
4 5/6 – 4 1/3
= 4 – 4 – 5/6 – 1/3
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 6 is the least common multiple of denominators 6 and 3. Use it to convert to equivalent fractions with this common denominator.
= 0 – (5 – 2)/6
= 3/6
= 1/2
Therefore, the answer is 1/2
Problem Solving
Question 4.
Mrs Gabel bought 7\(\frac{5}{6}\) gallons of punch for the class party. The students drank 4\(\frac{1}{2}\) gallons of punch. How much punch was left at the end of the party? Write in simplest form.
Answer:
The above-given:
The number of gallons of punch Gabel bought for the party = 7 5/6
The number of gallons of punch students drank = 4 1/2
The number of gallons of punch left = p
p = 7 5/6 – 4 1/2
p = 7 – 4 – 5/6 – 1/2
p = 3 – 5/6 – 1/2
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 6 is the least common multiple of denominators 6 and 2. Use it to convert to equivalent fractions with this common denominator.
p = 3 – (5 – 3)/6
p = 3 – 2/6
p = 3 – 1/3
This can also be written as 3 1/3
Therefore, 3 1/3 gallons of punch was left at the end of the party.
Question 5.
Bella is 10\(\frac{5}{12}\) years old. Franco is 12\(\frac{7}{12}\) years old. What is the difference in their ages? Write in simplest form.
Answer:
The above-given:
The number of years old the Bella is = 10 5/12
The number of years old Franco was = 12 7/12
The difference in their ages = a
a = 12 7/12 – 10 5/12
Here denominators are the same so we have to subtract directly.
a = 12 – 10 – 7/12 – 5/12
a = 2 – (7 – 5)/12
a = 2 – 2/12
a = 2 – 1/6
a = 2 1/6.
Therefore, the difference is 2 1/6
Question 6.
In one week, the fifth grade class recycled 9\(\frac{2}{3}\) pounds of glass and 12\(\frac{3}{4}\) pounds of newspaper. How many more pounds of a newspaper than glass did the class recycle?
Answer:
The above-given:
The number of pounds of glass recycled by the fifth grade = 9 2/3
The number of pounds of newspapers recycled = 12 3/4
The number of more pounds of newspaper recycled than glass = R
R = 12 3/4 – 9 2/3
R = 12 – 9 – 3/4 – 2/3
R = 3 – 3/4 – 2/3
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 12 is the least common multiple of denominators 3 and 4. Use it to convert to equivalent fractions with this common denominator.
R = 3 – (9 – 8)/12
R = 3 – 1/12
R = 3 1/12
Therefore, 3 1/4 pounds of the newspaper is recycled than glass.
Question 7.
Mathematical PRACTICE 2 Use Number Sense A snack mix recipe calls for 5\(\frac{3}{4}\) cups of cereal and 3\(\frac{5}{12}\) cups less of raisins. How many cups of raisins are needed? Write in simplest form.

Answer:
The above-given:
The number of cups of cereal mixed for a snack = 5 3/4
The number of cups of raisins less = 3 5/12
The number of cups of raisins needed = c
c = 5 3/4 – 3 5/12
c = 5 – 3 – 3/4 – 5/12
c = 2 – 3/4 – 5/12
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 12 is the least common multiple of denominators 4 and 12. Use it to convert to equivalent fractions with this common denominator.
c = 2 – (9 – 5)/12
c = 2 – 4/12
c = 2 – 1/3
c = 2 1/3
Therefore, 2 1/3 cups of raisins are needed.
Test Practice
Question 8.
What is the difference between the two weights?

A. \(\frac{1}{2}\) ounce
B. \(\frac{7}{8}\) ounce
C. 1\(\frac{3}{8}\) ounces
D. 1\(\frac{7}{8}\) ounces
Answer: Option C is the correct answer
Explanation:
The above-given weights:
The weight of the phone = 4 1/2
The weight of the remote = 3 1/8
The difference between the objects = d
d = 4 1/2 – 3 1/8
d = 4 – 3 – 1/2 – 1/8
d = 1 – 1/2 – 1/8
here the denominators are not equal so we have to make the denominators equal.
– Find the common denominator.
– 8 is the least common multiple of denominators 2 and 8. Use it to convert to equivalent fractions with this common denominator.
d = 1 – (4 – 1)/8
d = 1 – 3/8
d = 1 3/8
Therefore, the difference between the weights is 1 3/8 ounces.