All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 11 Add Mixed Numbers will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 11 Add Mixed Numbers
Math in My World
Example 1
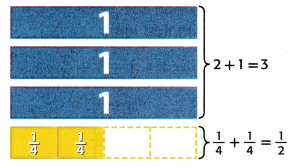
A hammerhead shark swam 2\(\frac{1}{4}\) miles. The next day, it swam 1\(\frac{1}{4}\) miles. How many miles did it swim altogether?
Find 2\(\frac{1}{4}\) + 1\(\frac{1}{4}\).
Estimate 2\(\frac{1}{4}\) + 1\(\frac{1}{4}\) ≈ 2 + 1, or 3
2\(\frac{1}{4}\) + 1\(\frac{1}{4}\) = 1 + 1 + \(\frac{1}{4}\) + 1 + \(\frac{1}{4}\) Write as a sum of wholes and fractions.
= 1 + 1 + 1 + \(\frac{1}{4}\) + \(\frac{1}{4}\) Group the wholes and the fractions together.
= 3 + \(\frac{2}{4}\) 1 + 1 + 1 = 3 and \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\)
= 
Write in simplest form. \(\frac{2}{4}\) = \(\frac{1}{2}\)
So, the hammerhead shark swam miles.
The models show that 2\(\frac{1}{4}\) + 1\(\frac{1}{4}\) = 3\(\frac{1}{2}\)
Check Compared to the estimate, 3\(\frac{1}{2}\) ≈ 3. The answer is reasonable.
Answer:
The process is given above:
The number of miles hammerhead shark swim = 2 1/4
The number of miles hammerhead sharks swim on the next day = 1 1/4
The total number of miles a shark travels altogether = X
X = 2 1/4 + 1 1/4
X = 2 + 1 + 1/4 + 1/4
X = 3 + 2/4
X = 3 + 1/2
X = 3 1/2.
Therefore, the shark travels altogether is 
miles.
Example 2
The diagram shows the length of a sea turtle. What is the total length of the sea turtle?
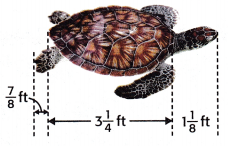
Find \(\frac{7}{8}\) + 3\(\frac{1}{4}\) + 1\(\frac{1}{8}\).
1. Write an equivalent fraction for 3\(\frac{1}{4}\) so that the fractions all have the same denominator. The LCD is 8.
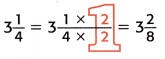
Write an equivalent fraction with a denominator of 8.
2. Add.
\(\frac{7}{8}\) + 3\(\frac{1}{4}\) + 1\(\frac{1}{8}\) = \(\frac{7}{8}\) + 3\(\frac{2}{8}\) + 1\(\frac{1}{8}\) Write 3\(\frac{1}{4}\) as 3\(\frac{2}{8}\)
= 3 + 1 + \(\frac{7}{8}\) + \(\frac{2}{8}\) + \(\frac{1}{8}\) Group the wholes and the fractions together.
= 4 + \(\frac{10}{8}\) 3 + 1 = 4 and \(\frac{7}{8}\) + \(\frac{2}{8}\) + \(\frac{1}{8}\) = \(\frac{10}{8}\)
= 4 + 1\(\frac{2}{8}\) Write \(\frac{10}{8}\) as \(\frac{8}{8}\) + \(\frac{2}{8}\), or 1\(\frac{2}{8}\)
= 
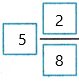Write in simplest form. 4 + 1 = 5 and \(\frac{2}{8}\) = \(\frac{1}{4}\)
So, \(\frac{7}{8}\) + 3\(\frac{1}{4}\) + 1\(\frac{1}{8}\) =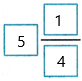 
The total length of the sea turtle is feet.
Guided Practice
Question 1.
Estimate, then add. Write the sum in simplest form.
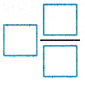
3\(\frac{3}{8}\) + 2\(\frac{1}{2}\) = 1 + 1 + 1 + \(\frac{3}{8}\) + 1 + 1 + \(\frac{4}{8}\).
= 
Answer:
The above-given mixed fractions:
3 3/8 + 2 1/2
Now simplify the equation:
= 3 + 2 + 3/8 + 1/2
= 5 + 3/8 + 1/2
In fractions, make the denominators the same. So what we do is, take LCM.
8 is the least common multiple of denominators 8 and 2. Use it to convert to equivalent fractions with this common denominator.
= 5 + (3 + 4)/8
= 5 + 7/8
= 5 7/8
Therefore, 3\(\frac{3}{8}\) + 2\(\frac{1}{2}\) =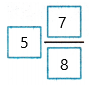 
Talk Math
Explain how to simplify 3\(\frac{6}{4}\)
Answer:
Go through the step-by-step procedure given below to understand how to simplify fractions.
Step 1: Write the factors of the numbers which are there in the numerator and denominator.
Step 2: Identify the common factors of both the numerator and denominator.
Step 3: In this step, we have to divide the numerator and denominator by the common factors until they have no common factor other than 1.
The above-given fraction:
3 6/4
6/4 is not simplified 2 is a common factor of 6 and 4.
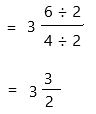
Note: After simplifying a fraction, it is always important to check the result to make sure that the numerator and denominator do not have any more factors in common. Remember, the definition of a simplified fraction: a fraction is considered simplified if there are no common factors in the numerator and denominator.
Independent Practice
Estimate, then add. Write each sum in simplest form.
Question 2.
4\(\frac{3}{5}\) + 3\(\frac{1}{5}\) = ____
Answer:
The above-given mixed fractions:
4 3/5 + 3 1/5
Here denominators are the same. So we can directly add the fractions.
= 4 + 3 + 3/5 + 1/5
= 7 + 4/5
= 7 4/5
Therefore, 4\(\frac{3}{5}\) + 3\(\frac{1}{5}\) =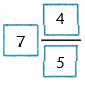 
Question 3.
7\(\frac{4}{11}\) + 2\(\frac{6}{11}\) = ____
Answer:
The above-given mixed fractions:
7 4/11 + 2 6/11
Here the denominators are the same. So we can add the fractions directly.
= 7 + 2 + 4/11 + 6/11
= 9 + 10/11
= 9 10/11
Therefore, 7\(\frac{4}{11}\) + 2\(\frac{6}{11}\) =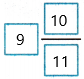 
Question 4.
5\(\frac{1}{12}\) + 6\(\frac{1}{4}\) = ____
Answer:
The above-given mixed fractions:
5 1/2 + 6 1/4
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
= 5 + 6 + 1/2 + 1/4
4 is the least common multiple of denominators 2 and 4. Use it to convert to equivalent fractions with this common denominator.
= 11 + (2 + 1)/4
= 11 + 3/4
This can be written as 11 3/4
Therefore, 5\(\frac{1}{12}\) + 6\(\frac{1}{4}\) =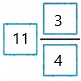 
Question 5.
8\(\frac{4}{15}\) + 3\(\frac{2}{15}\) = ____
Answer:
The above-given mixed fractions:
8 4/15 + 3 2/15
Here denominators are the same. So we can directly add the fractions.
= 8 + 3 + 4/15 + 2/15
= 11 + 6/15
6/15 is not simplified because 3 is a common factor of 6 and 15.
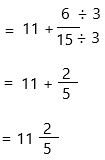
Note: After simplifying a fraction, it is always important to check the result to make sure that the numerator and denominator do not have any more factors in common. Remember, the definition of a simplified fraction: a fraction is considered simplified if there are no common factors in the numerator and denominator.
Question 6.
6\(\frac{1}{9}\) + 2\(\frac{1}{3}\) = ____
Answer:
The above-given mixed fractions:
6 1/9 + 2 1/3
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
= 6 + 2 + 1/9 + 1/3
9 is the least common multiple of denominators 9 and 3. Use it to convert to equivalent fractions with this common denominator.
= 8 + (1 + 3)/9
= 8 + 4/9
= 8 4/9
Therefore, 6\(\frac{1}{9}\) + 2\(\frac{1}{3}\) =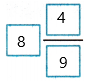 
Question 7.
5\(\frac{1}{3}\) + 6\(\frac{1}{2}\) = ____
Answer:
The above-given mixed fractions:
5 1/3 + 6 1/2
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
= 5 + 6 + 1/3 + 1/2
6 is the least common multiple of denominators 3 and 2. Use it to convert to equivalent fractions with this common denominator.
= 11 + (2 + 3)/6
= 11 + 5/6
= 11 5/6
Therefore, 5\(\frac{1}{3}\) + 6\(\frac{1}{2}\) =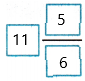 
Question 8.
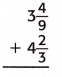
Answer:
The above-given fractions:
3 4/9 + 4 2/3
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
= 3 + 4 + 4/9 + 2/3
9 is the least common multiple of denominators 9 and 3. Use it to convert to equivalent fractions with this common denominator.
= 7 + (4 + 6)/9
= 7 + 10/9
10/9 is an improper fraction so we need to convert it into a mixed fraction.
– 10 ÷ 9 = 1 remainder 1
= 7 + 1 1/9
= 8 1/9.
Therefore,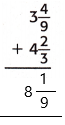 
Question 9.
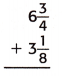
Answer:
The above-given mixed fractions:
6 3/4 + 3 1/8
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
= 6 + 3 + 3/4 + 1/8
8 is the least common multiple of denominators 4 and 8. Use it to convert to equivalent fractions with this common denominator.
= 9 + (6 + 1)/8
= 9 + 7/8
= 9 7/8
Therefore,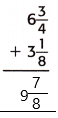 
Question 10.
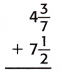
Answer:
The above-given mixed fractions:
4 3/7 + 7 1/2
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
= 4 + 7 + 3/7 + 1/2
14 is the least common multiple of denominators 7 and 2. Use it to convert to equivalent fractions with this common denominator.
= 11 + ( 6 + 7)/14
= 11 + 13/14
= 11 13/14.
Therefore,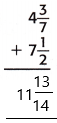 
Algebra Find each unknown.
Question 11.
9\(\frac{9}{10}\) + 7\(\frac{3}{5}\) = y
y = _____
Answer:
The above-given mixed fractions:
9 9/10 + 7 3/5 = y
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
y = 9 + 7 + 9/10 + 3/5
10 is the least common multiple of denominators 10 and 5. Use it to convert to equivalent fractions with this common denominator.
y = 16 + (9 + 6)/10
y = 16 + 15/10
15/10 = 3/2 {15/10 is not simplified because 5 is a common factor for 15 and 10}
3/2 in mixed fraction: 1 1/2
y = 16 + 1 1/2
y = 17 1/2.
Therefore, the value of y =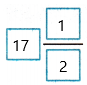 
Question 12.
14\(\frac{19}{20}\) + 8\(\frac{1}{4}\) = k
k = _____
Answer:
The above-given fractions:
14 19/20 + 8 1/4 = k
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
k = 14 + 8 + 19/20 + 1/4
20 is the least common multiple of denominators 20 and 4. Use it to convert to equivalent fractions with this common denominator.
k = 22 + ( 19 + 5)/20
k = 22 + 24/20
24/20 is not simplified because 4 is a common factor for 24 and 20
24/20: if we divide by 4 then we get 6/5
6/5 is an improper fraction. So we have to convert it into a mixed fraction.
6 ÷ 5 = 1 remainder 1.
The mixed fraction is 1 1/5
k = 22 + 1 1/5
k = 23 1/5
Question 13.
16\(\frac{11}{12}\) + 5\(\frac{2}{3}\) = d
d = _____
Answer:
The above-given mixed fraction:
16 11/12 + 5 2/3 = d
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
d = 16 + 5 + 11/12 + 2/3
12 is the least common multiple of denominators 12 and 3. Use it to convert to equivalent fractions with this common denominator.
d = 21 + (11 + 8)/12
d = 21 + 19/12
19/12 is an improper fraction so we have to convert it into a mixed fraction.
19 ÷ 12 = 1 remainder 7
This can be written as 1 7/12
d = 21 + 1 7/12
d = 22 7/12.
Problem Solving
Question 14.
Zita made 1\(\frac{5}{8}\) quarts of punch. Then she made 1\(\frac{7}{8}\) more quarts. How much punch did she make in all?
Answer:
The above-given:
The number of quarts of punch Zita made = 1 5/8
The number of quarts of more punch she made = 1 7/8
The total punch she makes = p
p = 1 5/8 + 1 7/8
p = 1 + 1 + 5/8 + 7/8
p = 2 + 12/8
p = 2 + 3/2
p = 2 3/2
Therefore, the total punch is 2 3/2 quarts.
Question 15.
Find five and two-eighths plus three and six-eighths. Write in words in simplest form.
Answer:
This can be written as:
5 2/8 + 3 6/8
Now simplify the equation:
5 + 3 + 2/8 + 6/8
As the denominators are the same, so we can add directly.
= 8 + 8/8
= 8 + 1
= 9
In word form, nine.
Question 16.
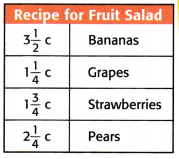
Mathematical PRACTICE 1 Make a Plan Tomas made fruit salad using the recipe. How many cups of fruit are needed altogether?
Answer:
The above-given:
The number of cups of banana = 3 1/2
The number of cups of grapes = 1 1/4
The number of cups of strawberry = 1 3/4
The number of cups of pears = 2 1/4
The total number of cups of fruits he used = x
x = 3 1/2 + 1 1/4 + 1 3/4 + 2 1/4
x = 3 + 1 + 1 + 2 + 1/2 + 1/4 + 1/4 + 1/4
x = 7 + 1/2 + 3/4
Make the denominators equal.
4 is the least common multiple of denominators 2 and 4. Use it to convert to equivalent fractions with this common denominator.
x = 7 + (2 + 3)/4
x = 7 + 5/4
5/4 is an improper fraction so convert it into mixed fractions.
5/4 = 1 1/4
x = 7 + 1 1/4
x = 8 1/4
Therefore, he used 8 1/4 cups of fruit to make a fruit salad.
HOT Problems
Question 17.
Mathematical PRACTICE 3 Find the Error Antwan is finding 4\(\frac{1}{5}\) + 2\(\frac{3}{5}\). Find and correct his mistake.
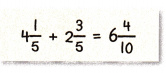
Answer:
The above-given equation:
4 1/5 + 2 3/5
Now simplify the equation:
= 4 + 2 + 1/5 + 3/5
as the denominators are equal so we can directly add the fractions.
= 6 + 4/5
= 6 4/5
Therefore, 6 4/5 is the correct answer.
Question 18.
? Building on the Essential Question How can equivalent fractions help when adding mixed numbers?
Answer:
– It can help by when finding the LCD (Least Common Denominator) you find the least number they have in common then that number is your equivalent fraction.
* The least common denominator (LCD) is the smallest number that can be a common denominator for a set of fractions.
McGraw Hill My Math Grade 5 Chapter 9 Lesson 11 My Homework Answer Key
Practice
Estimate, then add. Write each sum in simplest form.
Question 1.
2\(\frac{1}{10}\) + 5\(\frac{7}{10}\) = ____
Answer:
The above-given mixed fractions:
2 1/10 + 5 7/10
Now simplify the equation:
= 2 + 5 + 1/10 + 7/10
= 7 + 1/10 + 7/10
as the denominators are the same so we can directly add the fractions.
= 7 + 8/10
8/10 is not simplified because 2 is a common factor of 8 and 10.
8/10 = if we divide by 2 then we get 4/5
= 7 + 4/5
* A mixed fraction a b/c can also be written as a + (b/c).
= 7 4/5.
Therefore, 2\(\frac{1}{10}\) + 5\(\frac{7}{10}\) = 7 4/5.
Question 2.
9\(\frac{3}{4}\) + 8\(\frac{3}{4}\) = ____
Answer:
The above-given mixed fractions:
9 3/4 + 8 3/4
= 9 + 8 + 3/4 + 3/4
= 17 + 6/4
6/4 is divided by 2 because 2 is a common factor of 6 and 4.
6/4 = 3/2
= 17 + 3/2
3/2 is an improper fraction so convert it into a mixed fraction.
3/2 = 1 remainder = 1
3/2 in the mixed fraction is 1 1/2
Finally, 17 + 1 1/2
= 18 1/2
Therefore, 9\(\frac{3}{4}\) + 8\(\frac{3}{4}\) = 18 1/2.
Question 3.
3\(\frac{5}{8}\) + 6\(\frac{1}{2}\) = ____
Answer:
The above-given mixed fraction:
3 5/8 + 6 1/2
= 3 + 6 + 5/8 + 1/2
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
= 9 + 5/8 + 1/2
8 is the least common multiple of denominators 8 and 2. Use it to convert to equivalent fractions with this common denominator.
= 9 + ( 5 + 4)/8
= 9 + 9/8
9/8 is an improper fraction, so convert it into a mixed fraction.
9/8 = 1 remainder = 1
The mixed fraction can be written as 1 1/8.
= 9 + 1 1/8
= 10 1/8
Therefore, 3\(\frac{5}{8}\) + 6\(\frac{1}{2}\) = 10 1/8.
Question 4.
1\(\frac{1}{12}\) + 4\(\frac{5}{12}\) = ____
Answer:
The above-given mixed fractions:
1 1/12 + 4 5/12
Here denominators are the same so we can add fractions directly.
= 1 + 4 + 1/12 + 5/12
= 5 + 6/12
= 5 + 1/2
* A mixed fraction a b/c can also be written as a + (b/c).
= 5 1/2
Therefore, 1\(\frac{1}{12}\) + 4\(\frac{5}{12}\) = 5 1/2.
Question 5.
11\(\frac{3}{5}\) + 6\(\frac{4}{15}\) = ____
Answer:
The above-given fractions:
11 3/5 + 6 4/15
= 11 + 6 + 3/5 + 4/15
= 17 + 3/5 + 4/15
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
15 is the least common multiple of denominators 5 and 15. Use it to convert to equivalent fractions with this common denominator.
= 17 + (9 + 4)/15
= 17 + 13/15
* A mixed fraction a b/c can also be written as a + (b/c).
= 17 13/15.
Therefore, 11\(\frac{3}{5}\) + 6\(\frac{4}{15}\) = 17 13/15.
Question 6.
9\(\frac{1}{2}\) + 12\(\frac{11}{20}\) = ____
Answer:
The above-given mixed fractions:
9 1/12 + 12 11/20
9 + 12 + 1/12 + 11/20
= 21 + 1/12 + 11/20
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
60 is the least common multiple of denominators 12 and 20. Use it to convert to equivalent fractions with this common denominator.
= 21 + (5 + 33)/60
= 21 + 38/60
38/60 is not simplified because 2 is a common factor of 38 and 60
38/60 is divided by 2 then we get 19/30
= 21 + 19/30
* A mixed fraction a b/c can also be written as a + (b/c).
= 21 19/30.
Problem Solving
Question 7.
A flower is 9\(\frac{3}{4}\) inçhes tall. In one week, it grew 1\(\frac{1}{8}\) inches. How tall is the flower at the end of the week? Write in simplest form.
Answer:
The above-given:
The number of inches is a flower tall = 9 3/4
The number of inches it grew = 1 1/8
The number of inches a flower is tall at the end of the week = x
x = 9 3/4 + 1 1/8
x = 9 + 1 + 3/4 + 1/8
x = 10 + 3/4 + 1/8
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
8 is the least common multiple of denominators 4 and 8. Use it to convert to equivalent fractions with this common denominator.
x = 10 + (6 + 1)/8
x = 10 + 7/8
x = 10 7/8
Therefore, a flower grows 10 7/8 inches at the end of the week.
Question 8.
Find ten and three-sevenths plus eighteen and two-sevenths. Write in words in simplest form.
Answer:
The above-given:
10 3/7 + 18 2/7
10 + 18 + 3/7 + 2/7
= 28 + 3/7 + 2/7
here the denominators are the same so we can directly add the fractions.
= 28 + 5/7
= 28 5/7.
In word form, we can write as twenty-eight and five-sevenths.
Question 9.
Mathematical PRACTICE 6 Explain to a Friend Connor is filling a 15-gallon wading pool. On his first trip, he carried 3\(\frac{1}{12}\)– gallons of water. He carried 3\(\frac{5}{6}\) gallons on his second trip and 3\(\frac{1}{2}\) gallons on his third trip. Suppose he carries 5 gallons on his next trip. Will the pool be filled? Explain.
Answer:
The above-given:
The number of gallons a wading pool = 15
The number of gallons of water he carried on the first trip = 3 1/12
The number of gallons of water he carried on the second trip = 3 5/6
The number of gallons of water he carried on the third trip = 3 1/12
if he carries 5 gallons on the fourth trip, is the pool filled = x
x = 3 1/12 + 3 5/6 + 3 1/12
x = 3 + 3 + 3 + 1/12 + 5/6 + 1/12
x = 9 + 2/12 + 5/6
x = 9 + 1/6 + 5/6 { 2/12 = 1/6 (divided by 2) }
Here the denominators are the same so we can add the fractions directly.
x = 9 + 6/6
x = 9 + 1
x = 10
up to three trips 10 gallons are carried by him.
On the next trip, he takes 5 gallons: 10 + 5 = 15 gallons.
Therefore, the warden pool is filled with 15 gallons of water.
Test Practice
Question 10.
Benjamin had 2\(\frac{1}{3}\) gallons of fruit punch left after a party. He had 1\(\frac{3}{4}\) gallons of lemonade left. How many total gallons did he have left?
A. 4\(\frac{1}{12}\) gallons
B. 3\(\frac{1}{12}\)– gallons
C. 1\(\frac{5}{12}\)– gallons
D. \(\frac{5}{12}\)– gallon
Answer: Option A is the correct answer.
Explanation:
The above-given:
The number of gallons of fruit punch left after a party = 2 1/3
The number of gallons of lemonade left = 1 3/4
The total number of gallons he left = x
x = 2 1/3 + 1 3/4
x = 2 + 1 + 1/3 + 3/4
x = 3 + 1/3 + 3/4
Here the denominators are not the same. So we have to find the equivalent denominators.
– Find the common denominators:
12 is the least common multiple of denominators 4 and 3. Use it to convert to equivalent fractions with this common denominator.
x = 3 + (4 + 9)/12
x = 3 + 13/12
13/12 is an improper fraction so convert it into a mixed fraction.
13/12 = 1 remainder = 1
The mixed fraction can be written as 1 1/12
x = 3 + 1 1/12
x = 4 1/12
Therefore, he left with 4 1/12 gallons.