All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 10 Use Models to Add Mixed Numbers will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 10 Use Models to Add Mixed Numbers
You can use fraction circles to add mixed numbers.
Draw It
Find 2\(\frac{1}{3}\) + 1\(\frac{1}{3}\).
1. Shade and label the fraction circles to represent each mixed number.
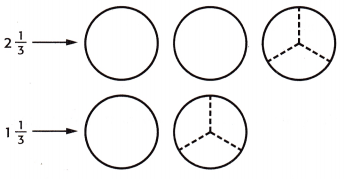
2. Combine whole numbers and fractions.
How many are whole fraction circles there altogether? ____
How many thirds are there altogether? ____
Add the whole numbers and the fractions.
2\(\frac{1}{3}\) + 1\(\frac{1}{3}\) = 1 + 1 + \(\frac{1}{3}\) + 1 + \(\frac{1}{3}\)
= 1 + 1 + 1 + \(\frac{1}{3}\) + \(\frac{1}{3}\) Group the whole numbers and fractions together.
= 3 + \(\frac{2}{3}\)
= 3\(\frac{2}{3}\)
So, 2\(\frac{1}{3}\) + 1\(\frac{1}{3}\) = 
Answer:
1. Shaded the regions of the mixed number 2 1/3.
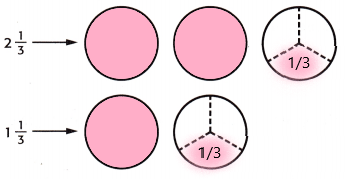
2. The number of the whole fraction circles together = 3
The number of thirds altogether = 2
Now add the whole numbers and fractions:
2 1/3 + 1 1/3
2 can be written as (1 + 1)
1 + 1 + 1 + 1/3 + 1/3
3 + 2/3
= 3 2/3
Therefore, 2 1/3 + 1 1/3 = 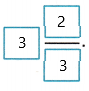
Try It
Find 1\(\frac{7}{8}\) + 1\(\frac{1}{2}\)
1. Shade and label the fraction circles to represent each mixed number. Write 1\(\frac{1}{2}\) as the equivalent fraction 1\(\frac{4}{8}\).
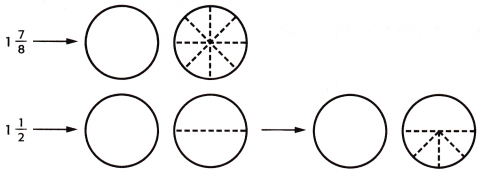
2. Combine whole numbers and fractions.
How many are whole fraction circles there altogether? ___
How many eighths are there altogether? ____
Add.
1\(\frac{7}{8}\) + 1\(\frac{4}{8}\) = 1 + \(\frac{7}{8}\) + 1 + \(\frac{4}{8}\)
= 1 + 1 + \(\frac{7}{8}\) + \(\frac{4}{8}\) Group the whole numbers and the fractions together.
= 2 + \(\frac{11}{8}\)
= 2 + 1\(\frac{3}{8}\) write \(\frac{11}{8}\) as \(\frac{8}{8}\) + \(\frac{3}{8}\), or 1\(\frac{3}{8}\)
= 3\(\frac{3}{8}\)
So, 1\(\frac{7}{8}\) + 1\(\frac{1}{2}\) = 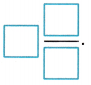
Answer:
1. shade the regions of the fraction circles to represent each mixed number.
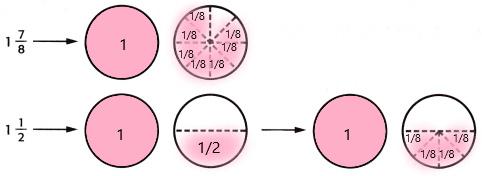
2. The number of whole fraction circles together = 3
The number of eighths together = 11
add:
1 7/8 + 1 1/2
= 1 + 1 + 7/8 + 4/8
= 2 + 11/8
11/8 in the mixed fraction is 1 3/8
= 2 + 1 3/8
= 3 3/8
Therefore, 1 7/8 + 1 1/2 = 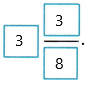
Talk About It
Question 1.
Mathematical PRACTICE 3 Draw a Conclusion Refer to Step 1 of the above activity. Explain why it was necessary to write 1\(\frac{1}{2}\) as 1\(\frac{4}{8}\).
Answer:
I need to find an equivalent fraction so that the denominators are the same.
Practice It
Shade the fraction circles to represent each mixed number. Then find each sum.
Question 2.
1\(\frac{1}{5}\) + 2\(\frac{3}{5}\) = ____
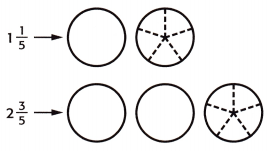
Answer:
1. shade the regions of the fraction circles to represent each mixed number.
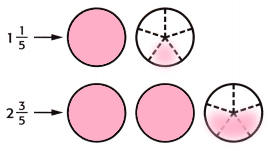
2. The number of whole fraction circles together = 3
The number of fifths together = 4
add:
1 1/5 + 2 3/5
1 + 2 + 1/5 + 3/5
3 + 4/5
= 3 4/5
Therefore, 1 1/5 + 2 3/5 = 3 4/5.
Question 3.
2\(\frac{5}{6}\) + 1\(\frac{1}{6}\) = ____
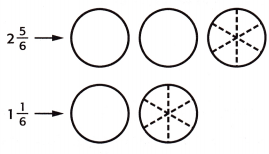
Answer:
1. shade the regions of the fraction circles to represent each mixed number.
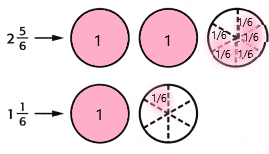
2. The number of whole fraction circles together = 3
The number of sixths together = 6
add:
2 5/6 + 1 1/6
= 2 + 1 + 5/6 + 1/6
= 3 + 6/6
= 3 + 1
= 4
Therefore, 2\(\frac{5}{6}\) + 1\(\frac{1}{6}\) = 4.
Question 4.
2\(\frac{2}{3}\) + 1\(\frac{1}{2}\) = ____
Answer:
1. shade the regions of the fraction circles to represent each mixed number.
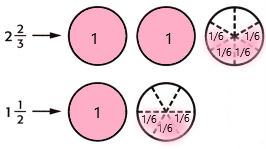
2. The number of whole fraction circles together = 3
The number of sixths together = 7
add:
2 2/3 + 1 1/2
if we convert mixed numbers to improper fractions.
2 2/3 = 3 x 2/3 + 2/3 = 6 + 2/3 = 8/3
1 1/2 = 2 x 1/2 + 1/2 = 2/2 + 1/2 = 3/2
Now add the improper fractions:
8/3 + 3/2
– 6 is the least common multiple of denominators 3 and 2. Use it to convert to equivalent fractions with this common denominator.
= 8 x 2/3 x 2 + 3 x 3/2 x 3
= 16/6 + 9/6
= 25/6
Step 2: Reduce the fraction to the lowest terms.
– 1 is the greatest common divisor of 25 and 6. The result can’t be further reduced.
so, what we do is: Convert improper fractions to mixed number
25/6 = 4 1/6 { 25 ÷ 6 = 4 remainder 1 }
Therefore, 2\(\frac{2}{3}\) + 1\(\frac{1}{2}\) = 4 1/6.
Question 5.
2\(\frac{7}{8}\) + 1\(\frac{1}{4}\) = ____
Answer:
1. shade the regions of the fraction circles to represent each mixed number.
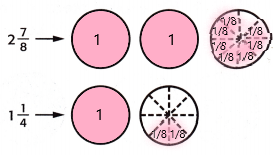
2. The number of whole fraction circles together = 3
The number of eighths together = 9
add:
2 7/8 + 1 1/4
Now convert mixed fraction to improper fraction
2 7/8 = 2 x 8/8 + 7/8 = 16/8 + 7/8 = 16 + 7/8 = 23/8
1 1/4 = 4 x 1/4 + 1/4 = 4 + 1/4 = 5/4
– Find the common denominator:
23/8 + 5/4
8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
= 23 x 1/8 x 1 + 5 x 2/4 x 2
= 23/8 + 10/8
= 23 + 10/8
= 33/8
Now reduce a fraction to the lowest terms.
– 1 is the greatest common divisor of 33 and 8. The result can’t be further reduced.
so, what we do is: Convert improper fractions to mixed number
33/8 = 4 1/8 { 33 ÷ 8 = 4 remainder 1 }
Therefore, 2\(\frac{7}{8}\) + 1\(\frac{1}{4}\) = 4 1/8.
Question 6.
2\(\frac{1}{2}\) + 2\(\frac{1}{4}\) = ____

Answer:
1. shade the regions of the fraction circles to represent each mixed number.
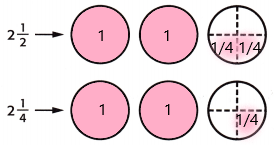
2. The number of whole fraction circles together = 4
The number of fourths together = 3
add:
2 1/2 + 2 1/4
= 2 + 2 + 1/2 + 1/4
= 4 + (2 + 1)/4
= 4 + 3/4
= 4 3/4
Therefore, 2\(\frac{1}{2}\) + 2\(\frac{1}{4}\) = 4 3/4.
Question 7.
2\(\frac{3}{4}\) + 2\(\frac{1}{8}\) = ____
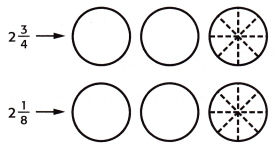
Answer:
1. shade the regions of the fraction circles to represent each mixed number.
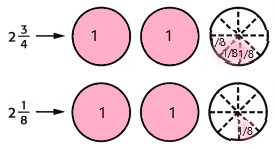
2. The number of whole fraction circles together = 4
The number of eighths together = 4
add:
2 3/4 + 2 1/8
= 2 + 2 + 3/4 + 1/8
= 4 + (6 + 1)/8
= 4 + 7/8
= 4 7/8
Therefore, 2\(\frac{3}{4}\) + 2\(\frac{1}{8}\) = 4 7/8
Apply It
Mathematical PRACTICE 5 Use Math Tools Use fraction circles to solve Exercises 8 and 9.
Question 8.
Eduardo worked 1\(\frac{1}{2}\) hours on Monday, 1\(\frac{1}{2}\) hours on Tuesday, and 2\(\frac{1}{2}\) hours on Wednesday. How many hours did he work in all?
Answer:
The above-given:
The number of hours Eduardo worked on Monday = 1 1/2
The number of hours Eduardo worked on Tuesday = 1 1/2
The number of hours Eduardo worked on Wednesday = 2 1/2
The total number of hours he worked = X
X = 1 1/2 + 1 1/2 + 2 1/2
X = 1 + 1 + 2 + 1/2 + 1/2 + 1/2
X = 4 + 3/2
X = 4 3/2
Therefore, the total number of hours he worked was 4 3/2.
Question 9.
Marissa walked 1\(\frac{1}{4}\) miles to the store. She walked the same distance back home. How far did Marissa walk altogether?
Answer:
The above-given:
The number of miles Marissa walked to the store = 1 1/4
From the store to the home she walked the same distance ( 1 1/4)
The total number of miles she walked = X
X = 1 1/4 + 1 1/4
X = 1 + 1 + 1/4 + 1/4
X = 2 + 2/4
X = 2 + 1/2
X = 2 1/2
Therefore, the total number of miles she walked was 2 1/2.
Question 10.
Mathematical PRACTICE 4 Model Math Write and solve a real-world problem that could be represented by the fraction circles shown.
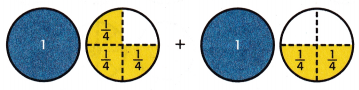
Answer:
a sample answer is given:
The real-world example will be
Marissa walked 1\(\frac{3}{4}\) miles to the store. She walked 1\(\frac{2}{4}\) miles the back home. How far did Marissa walk altogether?
The equation can be written as 1 3/4 + 1 2/4
Now add the equation:
1 + 1 + 3/4 + 2/4
2 + 5/4
The total number of miles she walked was 2 5/4.
Write About It
Question 11.
How can I use fractions circles to find the sum of mixed numbers?
Answer:
We can clearly know the whole fractions or portions of a whole. That means 1/2, 1/4, 2/3, 3/4, 1/3 and so on…
In circles, we can easily represent the parts of fractions and simplify the mixed numbers.
The circles for the mixed fractions in this shaded region in the right-most of each diagram represent the numerator of the mixed fraction so that we can have a clear idea of the numerator and the unshaded region is the remaining part.
McGraw Hill My Math Grade 5 Chapter 9 Lesson 10 My Homework Answer Key
Practice
Question 1.
Shade the fraction circles to represent each mixed number. Then find the sum.

Answer:
1. shade the regions of the fraction circles to represent each mixed number.

2. The number of whole fraction circles together = 2
The number of sixths together = 4
add:
1 1/2 + 1 2/3
= 1 + 1 + 1/2 + 2/3
= 2 + (3 + 4)/6
= 2 + 7/6
= 2 + 1 1/6
= 3 1/6
Therefore, 1 1/2 + 1 2/3 = 3 1/6.
Question 2.
Shade the fraction circles to represent each mixed number. Then find the sum.
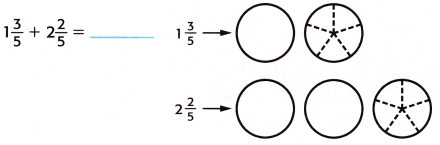
Answer:
1. shade the regions of the fraction circles to represent each mixed number.
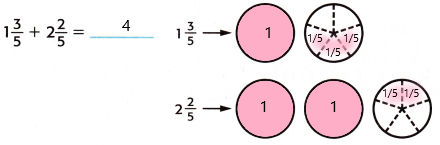
2. The number of whole fraction circles together = 3
The number of fifths together = 5
add:
1 3/5 + 2 2/5
= 1 + 2 + 3/5 + 2/5
= 3 + 5/5
= 3 + 1
= 4
Therefore, 1 3/5 + 2 2/5 = 4
Problem Solving
Question 3.
Andrew spent 1\(\frac{1}{6}\) hours studying for his science exam. He spent another 1\(\frac{1}{2}\) hours studying for his history exam. How many total hours did Andrew spend studying for his exams? Draw fraction circles to solve.
Answer:
The above-given:
The number of hours Andrew spent for studying his science exam = 1 1/6
The number of hours Andrew spent for studying his history exam = 1 1/2
The total number of hours she spent on both subjects = X
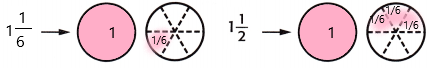
X = 1 1/6 + 1 1/2
X = 1 + 1 + 1/6 + 1/2
X = 2 + (1 + 3) / 6
X = 2 + 4/6
X = 2 + 2/3
X = 2 2/3.
Therefore, he spent 2 2/3 hours on both subjects.
Question 4.
Kimberly used 1\(\frac{1}{3}\) cups of sugar to bake a cake and 2\(\frac{3}{4}\) cups of sugar to make cookies. How many total cups of sugar did she use?
Answer:
The above-given:
The number of cups of sugar used by Kimberly to make a cake = 1 1/3
The number of cups of sugar used by Kimberly to make cookies = 2 3/4
The total number of cups of sugar she used = X
X = 1 1/3 + 2 3/4
X = 1 + 2 + 1/3 + 3/4
X = 3 + (4 + 9)/12
X = 3 + 13/12
X = 3 + 1 1/12
X = 4 1/12
Therefore, she used 4 1/12 cups of sugar.
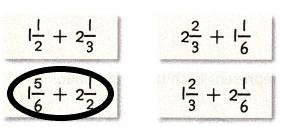
Question 5.
Mathematical PRACTICE 3 Which One Doesn’t Belong? Find each sum by drawing fraction circles. Then circle the expression that does not belong. Explain.
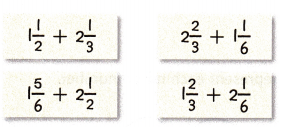
Answer:
The above-given:
1 1/2 + 2 1/3 = 1 + 2 + 1/2 + 1/3 = 3 + (3 + 2)/6 = 3 + 5/6 = 3 5/6
2 2/3 + 1 1/6 = 2 + 1 +2/3 + 1/6 = 3 + (4 + 1)/6 = 3 + 5/6 = 3 5/6
1 5/6 + 2 1/2 = 1 + 2 + 5/6 + 1/2 = 3 + (5 + 3)/6 = 3 + 8/6 = 3 + 4/3 = 3 4/3
1 2/3 + 2 1/6 = 1 + 2+ 2/3 + 1/6 = 3 + (4 + 1)/6 = 3 + 5/6 = 3 5/6