All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 1 Round Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 1 Round Fractions
You can use benchmark fractions, such as \(\frac{1}{2}\), to round a fraction to 0, \(\frac{1}{2}\), or 1.
Math in My World
Example 1
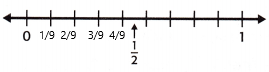
A poison dart frog is 2 inches long. This is equal to \(\frac{2}{12}\) foot. Is \(\frac{2}{12}\) closest to 0, \(\frac{1}{2}\), or 1?
Graph \(\frac{2}{12}\) on a number line. Mark off 12 equal increments from 0 to 1. You know \(\frac{1}{2}\) = \(\frac{6}{12}\).


Which number, 0, \(\frac{1}{2}\), or 1 is \(\frac{2}{12}\) closest to on the number line? ___
So, the length of a poison dart frog is closest to _____ feet.
Answer:

2/12 = 1/6
1/6 = 0.1666
1/6 is close to 0.
0 is closest to the number line.
Therefore, the length of a poison dart frog is closest to 0 feet.
Key Concepts Rounding Fractions
Round Down
If the numerator is much smaller than the denominator, round the fraction down to 0.
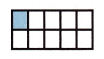
\(\frac{1}{10}\) rounds to 0.
Round to \(\frac{1}{2}\)
If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).

\(\frac{6}{10}\) rounds to \(\frac{1}{2}\).
Round Up
If the numerator is almost as large as the denominator, round the fraction up to 1.
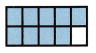
\(\frac{9}{10}\) rounds to 1.
Example 2
Round \(\frac{4}{9}\) to 0, \(\frac{1}{2}\), or 1.
The number 4\(\frac{1}{2}\) is half of 9.
The numerator in \(\frac{4}{9}\) is ____, which is very close to 4\(\frac{1}{2}\).
So, \(\frac{4}{9}\) rounds to 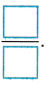
Check Graph \(\frac{4}{9}\) on a number line.
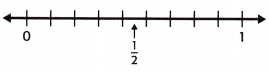
\(\frac{1}{2}\) is halfway between \(\frac{4}{9}\) and \(\frac{5}{9}\) since half of 9 is 4\(\frac{1}{2}\).
Answer:
The number 4 1/2 is half of the 9.
The numerator in 4/9 is 4, which is very close to 4 1/2.
Therefore, 4/9 rounds to 1/2.
Guided Practice
Graph each fraction on the number line. Then state whether each fraction is closest to 0, \(\frac{1}{2}\), or 1.
Talk Math
Tell how to round fractions in your own words.

Answer:
– Take any fraction.
– Convert the given fraction into decimals by dividing the numerator by the denominator.
– If the obtained number to the right of the decimal point is 0.5 or more, then add 1 to the left of the decimal point and remove the decimal part.
– If the obtained number to the right of the decimal point is lesser than 0.5, then leave the number to the left of the decimal point and remove the decimal part.
– Write the new number as a rounded number.
Question 1.
\(\frac{5}{6}\) ≈ ___
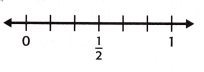
Answer:
The above-given fraction: 5/6
As per the above given key concepts, the rule is:
* If the numerator is almost as large as the denominator, round the fraction up to 1.
Hence, we can conclude that 5/6 is close to 1.
Question 2.
\(\frac{5}{8}\) ≈ ___
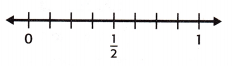
Answer:
The above-given fraction: 5/8
The number line:
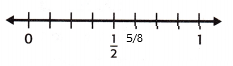
As per the above given key concepts, the rule is:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
From the above given key concept, the fraction 5/8 is close to 1/2.
Independent Practice
Round each fraction to 0, \(\frac{1}{2}\), or 1. Use a number line if needed.
Question 3.
\(\frac{1}{8}\) ≈ ___
Answer:
The above-given fraction: 1/8
The number line:
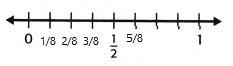
1/8 is close to the 0 on the number line. And also from the above key concepts, we can say that 1/8 is close to 0.
* If the numerator is much smaller than the denominator, round the fraction down to 0.
Question 4.
\(\frac{5}{9}\) ≈ ___
Answer:
The above-given fraction: 5/9
5/9 is close to the 1/2
* As per the above given key concepts, the rule is:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
Question 5.
\(\frac{7}{8}\) ≈ ___
Answer:
The above-given fraction: 7/8
The number line:
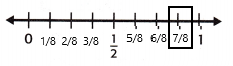
7/8 is close to 1 on the number line. And also from the above key concepts, we can say that 7/8 is close to 1.
* If the numerator is almost as large as the denominator, round the fraction up to 1.
Question 6.
\(\frac{3}{7}\) ≈ ___
Answer:
The above-given fraction: 3/7
3/7 is close to 1/2 on the number line.
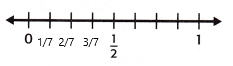
(or)
* As per the above given key concepts, the rule is:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
Question 7.
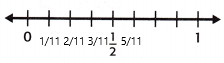
\(\frac{5}{11}\) ≈ ___
Answer:
The above-given fraction: 5/11
5/11 is closest to 1/2 on the number line:
(or)
* As per the above given key concepts, the rule is:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
Question 8.
\(\frac{4}{5}\) ≈ ___
Answer:
The above-given fraction: 4/5
4/5 is close to 1, from the above key concepts, we can say that 4/5 is close to 1.
* If the numerator is almost as large as the denominator, round the fraction up to 1.
Question 9.
\(\frac{1}{9}\) ≈ ___
Answer:
The above-given fraction: 1/9
1 is numerator and the 9 is denominator.
1 is smaller than 9.
* If the numerator is much smaller than the denominator, round the fraction down to 0.
From the above statement, we can say that the fraction 1/9 is close to 0.
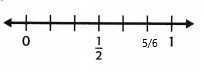
Question 10.
\(\frac{6}{7}\) ≈ ___
Answer:
The above-given fraction: 6/7
6/7 is close to 1.
The above concept rule:
* If the numerator is almost as large as the denominator, round the fraction up to 1.
6 is almost large as 7. As per the above statement, 6/7 is close to 1.
Question 11.
\(\frac{2}{5}\) ≈ ___
Answer:
The above-given fraction: 2/5
we go for the above key concepts:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
5 is half of the 2.5
Therefore, we can conclude that the fraction 2/5 is close to 1/2.
Question 12.
\(\frac{3}{8}\) ≈ ___
Answer:
The above-given fraction: 3/8
we go for the above key concepts:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
8 is the half of 4.
Therefore, we can conclude that the fraction 3/8 is close to 1/2.
We can check on the number line also.

On the number line also we can see that the 3/8 is close to 1/2.
Question 13.
\(\frac{1}{5}\) ≈ ___
Answer:
The above-given fraction: 1/5
1 is numerator and the 9 is denominator.
1 is smaller than 5.
* If the numerator is much smaller than the denominator, round the fraction down to 0.
From the above statement, we can say that the fraction 1/5 is close to 0.
Question 14.
\(\frac{15}{16}\) ≈ ___
Answer:
The above-given fraction: 15/16
we go for the above-given concept rules:
* If the numerator is almost as large as the denominator, round the fraction up to 1.
15 is almost large as 16. Therefore, we can conclude that 15/16 is close to 1.
Problem Solving
Question 15.
Mathematical PRACTICE 6 Be Precise Round the length of the ribbon to 0 inches, \(\frac{1}{2}\) inch, or 1 inch.

Answer:
Actually, the length of the ribbon is close to 1/2 on the measuring scale.
The ribbon is 1 unit more than 1/2. So we can conclude that it is close to 1/2.
Question 16.
Corri has finished about \(\frac{3}{5}\) of her daily chores. Has she finished about half of her chores or almost all of them?
Answer:
The above-given:
The number of daily chores finished by Corri = 3/5
We need to say how much she finished, 1/2 or almost all.
If we go for the above-given concept rules:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
From the above statement, we can conclude that 3/5 is close to 1/2.
Finally, we can say that she had finished about 1/2.
Question 17.
Peter has read about \(\frac{12}{15}\) of his book. Has he read about half of his book or almost all of his book?
Answer:
The above-given:
The number of books Peter has read = 12/15
We need to say he read half of his book or almost all.
If we go the above-given concept rules:
* If the numerator is almost as large as the denominator, round the fraction up to 1.
12 is almost large as 15.
Therefore, we can conclude that he had read the books almost all.
HOT Problems
Question 18.
Mathematical PRACTICE 3 Which One Doesn’t Belong? Circle the fraction that does not belong with the other three. Explain your reasoning.
\(\frac{2}{11}\) \(\frac{8}{15}\) \(\frac{7}{13}\) \(\frac{5}{12}\)
Answer:
The above-given fractions: 2/11, 8/15, 7/13, 5/12
2/11 is close to 0 because as the above-given concept rule:
* If the numerator is much smaller than the denominator, round the fraction down to 0.
2 is smaller than 11.
The next fraction is 8/15
15 is half of the 7.5
as per the statement, If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\). Therefore, we can conclude that 8/15 is close to 1/2.
The next fraction: 7/13
13 is half of the 6.5
as per the statement, If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\). Therefore, we can conclude that 7/13 is close to 1/2.
The last fraction: 5/12
12 is half of the 6.
as per the statement, If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\). Therefore, we can conclude that 5/12 is close to 1/2.
Finally, 2/11 does not belong to this group.
Question 19.
? Building on the Essential Question Describe two different ways of rounding fractions.
Answer:
There are two ways of rounding fractions:
One way is by using a number line.
and another method:
– Take any fraction.
– Convert the given fraction into decimals by dividing the numerator by the denominator.
– If the obtained number to the right of the decimal point is 0.5 or more, then add 1 to the left of the decimal point and remove the decimal part.
– If the obtained number to the right of the decimal point is lesser than 0.5, then leave the number to the left of the decimal point and remove the decimal part.
– Write the new number as a rounded number.
McGraw Hill My Math Grade 5 Chapter 9 Lesson 1 My Homework Answer Key
Practice
Round each fraction to 0, \(\frac{1}{2}\), or 1. Use a number line if needed.
Question 1.
\(\frac{5}{9}\) ≈ _____
Answer:
The above-given fraction: 5/9.
9 is half of 4.5
As per the above-given concept rules:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
Therefore, we can conclude that 5/9 is close to 1/2.
or else we can draw a number line also.
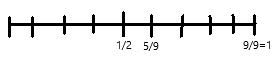
On the number line, 5/9 is close to 1/2.
Question 2.
\(\frac{1}{14}\) ≈ _____
Answer:
The above-given fraction: 1/14
1 is smaller than 14
As per the above-given concept statement:
* If the numerator is much smaller than the denominator, round the fraction down to 0.
Therefore, we can conclude that 1/14 is close to 0.
Question 3.
\(\frac{12}{13}\) ≈ _____
Answer:
The above-given fraction: 12/13
12 is almost large as 13.
Here we go for the concept rules that are given above:
* If the numerator is almost as large as the denominator, round the fraction up to 1.
Therefore, we can conclude that 12/13 is close to 1.
Question 4.
\(\frac{2}{13}\) ≈ _____
Answer:
The above-given fraction: 2/13
2 is smaller than 13.
As per the above-given concept statement:
* If the numerator is much smaller than the denominator, round the fraction down to 0.
Therefore, we can conclude that 2/13 is close to 0.
Question 5.
\(\frac{9}{11}\) ≈ _____
Answer:
The above-given fraction: 9/11
9 is almost large as 11.
Here we go for the concept rules that are given above:
* If the numerator is almost as large as the denominator, round the fraction up to 1.
Therefore, we can conclude that 9/11 is close to 1.
Question 6.
\(\frac{9}{17}\) ≈ _____
Answer:
The above-given fraction: 9/17
17 is half of 8.5
As per the above-given concept rules:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
Therefore, we can conclude that 9/17 is close to 1/2.
Problem Solving
Question 7.
Kevin ate \(\frac{5}{12}\) a pizza. Which is a better estimate for the amount of pizza that he ate: about half of the pizza or almost all of the pizza?
Answer:
The above-given:
The amount of pizza Kevin ate = 5/12
We need to estimate the amount of pizza that he ate 1/2 or almost all of the pizza.
12 is half of 6
As per the above-given concept rules:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
Therefore, we can conclude that he ate (1/2) half of the pizza.
Question 8.
Mathematical practice 1 Make Sense of Problems Darius has mowed \(\frac{1}{5}\) of his backyard. Which is a better estimate for how much of the lawn he has left to mow: almost all of the lawn or about half of the lawn?
Answer:
The above-given:
The amount of backyard that has been mowed by Darius = 1/5
We need to estimate how much lawn he has left to mow.
1 is smaller than 5
As per the above-given concept statement:
* If the numerator is much smaller than the denominator, round the fraction down to 0.
Therefore, we can conclude that 1/5 is close to 0.
Hence, he has to mow almost all of the lawn.
Question 9.
A bike path is 6\(\frac{3}{4}\) miles long. What whole number is closest to 6\(\frac{3}{4}\)?
Answer:
The above-given:
The number of miles a bike path long = 6 3/4
We need to find out the whole number that is closest to the 6 3/4.
3/4 is close to the 1.
Here we go for the concept rules that are given above:
* If the numerator is almost as large as the denominator, round the fraction up to 1.
as it was a mixed fraction, add 1 to the 6.
6 + 1 = 7
Therefore, 7 is closest to 6 3/4.
Question 10.
Savannah is making a quilt with squares having side lengths that are \(\frac{15}{16}\) foot each. Are the side lengths of the squares closer to \(\frac{1}{2}\) foot or 1 foot long?

Answer:
The above-given:
The side length of the foot = 15/16
15/16 is close to 1
Here we go for the concept rules that are given above:
* If the numerator is almost as large as the denominator, round the fraction up to 1.
Therefore, we can conclude that the side lengths of the square are close to 1.
Test Practice
Question 11.
Samantha shaded \(\frac{3}{7}\) of her design.
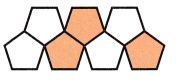
Which number is the best estimate for the shaded part of her design?
A. 0
B. \(\frac{1}{7}\)
C. \(\frac{1}{2}\)
D. 1
Answer: Option C is the correct answer.
The above-given fraction: 3/7
7 is half of 3.5
As per the above-given concept rules:
* If the numerator is about half of the denominator, round the fraction to \(\frac{1}{2}\).
Therefore, we can conclude that Samantha shaded 1/2 part of her design.