All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 9 Add and Subtract Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Add and Subtract Fractions
Essential Question
How can equivalent fractions help me add and subtract fractions?
Answer: Equivalent fractions are fractions that have different numerators and denominators but are equal to the same value. For example, 2/4 and 3/6 are equivalent fractions, because they both are equal to 1/2. Let us say, a/b and c/d are two fractions, after the simplification of these fractions, both result in equivalent fractions, say e/f, and then they are equal to each other.
Am I Ready?
Write each fraction in simplest form.
Question 1.
\(\frac{4}{8}\) = ____
Answer:
– The simplest form of a fraction is the fraction, whose numerator and denominator are relatively prime. It means the numerator (upper part or top) and denominator (lower part or bottom) of the fraction do not have any common factor between them, apart from 1.
– Finding the simplest form of any fraction is a simple method. We need to simplify the numerator and denominator of the fraction by dividing both the numerator and denominator by the greatest common factor that divides them completely. After division, both the numerator and denominator should remain whole numbers. This method of simplifying fractions is also known as reducing fractions.
The above-given fraction:
4/8
Find the greatest common factor (GCF) of 4 and 8. if it exists, and reduce our fraction by dividing both the numerator and denominator by it. GCF = 4, and getting our simplified answer:
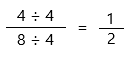
Therefore, the simplified answer is 1/2.
Question 2.
\(\frac{4}{12}\) = ____
Answer:
– The simplest form of a fraction is the fraction, whose numerator and denominator are relatively prime. It means the numerator (upper part or top) and denominator (lower part or bottom) of the fraction do not have any common factor between them, apart from 1.
– Finding the simplest form of any fraction is a simple method. We need to simplify the numerator and denominator of the fraction by dividing both the numerator and denominator by the greatest common factor that divides them completely. After division, both the numerator and denominator should remain whole numbers. This method of simplifying fractions is also known as reducing fractions.
The above-given fraction: 4/12
Find the greatest common factor (GCF) of 4 and 12. if it exists, reduce our fraction by dividing both the numerator and denominator by it. GCF = 4, and getting our simplified answer:
![]()
Therefore, the answer is 1/3.
Question 3.
\(\frac{15}{20}\) = ____
Answer:
– The simplest form of a fraction is the fraction, whose numerator and denominator are relatively prime. It means the numerator (upper part or top) and denominator (lower part or bottom) of the fraction do not have any common factor between them, apart from 1. A fraction is a value representing a part of a whole.
– Finding the simplest form of any fraction is a simple method. We need to simplify the numerator and denominator of the fraction by dividing both the numerator and denominator by the greatest common factor that divides them completely. After division, both the numerator and denominator should remain whole numbers. This method of simplifying fractions is also known as reducing fractions.
The above-given fraction: 15/20
Find the greatest common factor (GCF) of 15 and 20. if it exists, reduce our fraction by dividing both the numerator and denominator by it. GCF = 5, and getting our simplified answer:
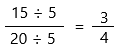
Therefore, the answer is 3/4.
Question 4.
\(\frac{4}{24}\) = ____
Answer:
– The simplest form of a fraction is the fraction, whose numerator and denominator are relatively prime. It means the numerator (upper part or top) and denominator (lower part or bottom) of the fraction do not have any common factor between them, apart from 1. A fraction is a value representing a part of a whole.
– Finding the simplest form of any fraction is a simple method. We need to simplify the numerator and denominator of the fraction by dividing both the numerator and denominator by the greatest common factor that divides them completely. After division, both the numerator and denominator should remain whole numbers. This method of simplifying fractions is also known as reducing fractions.
The above-given fraction: 4 /24
Find the greatest common factor (GCF) of 4 and 24. if it exists, reduce our fraction by dividing both the numerator and denominator by it. GCF = 4, and getting our simplified answer:
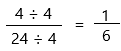
Therefore, the answer is 1/6.
Question 5.
\(\frac{16}{30}\) = ____
Answer:
– The simplest form of a fraction is the fraction, whose numerator and denominator are relatively prime. It means the numerator (upper part or top) and denominator (lower part or bottom) of the fraction do not have any common factor between them, apart from 1. A fraction is a value representing a part of a whole.
– Finding the simplest form of any fraction is a simple method. We need to simplify the numerator and denominator of the fraction by dividing both the numerator and denominator by the greatest common factor that divides them completely. After division, both the numerator and denominator should remain whole numbers. This method of simplifying fractions is also known as reducing fractions.
The above-given fraction: 16/30
Find the greatest common factor (GCF) of 16 and 30. if it exists, reduce our fraction by dividing both the numerator and denominator by it. GCF = 2, and getting our simplified answer:
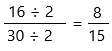
Therefore, the answer is 8/15.
Question 6.
\(\frac{24}{40}\) = ____
Answer:
– The simplest form of a fraction is the fraction, whose numerator and denominator are relatively prime. It means the numerator (upper part or top) and denominator (lower part or bottom) of the fraction do not have any common factor between them, apart from 1. A fraction is a value representing a part of a whole.
– Finding the simplest form of any fraction is a simple method. We need to simplify the numerator and denominator of the fraction by dividing both the numerator and denominator by the greatest common factor that divides them completely. After division, both the numerator and denominator should remain whole numbers. This method of simplifying fractions is also known as reducing fractions.
The above-given fraction: 24 / 40
Find the greatest common factor (GCF) of 24 and 40. if it exists, reduce our fraction by dividing both the numerator and denominator by it. GCF = 8, and getting our simplified answer:
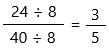
Therefore, the answer is 3/5.
Question 7.
Marcela made 4 out of 16 free throws. Write the fraction of free throws she made in simplest form.
Answer:
The above-given:
The total number of free throws = 16
The number of free throws Marcela made = 4
We need to write in a fraction form and simplify the answer.
The fraction form = number of throws / total throws.
The fraction form = 4 / 16
Find the greatest common factor (GCF) of 4 and 16. if it exists, reduce our fraction by dividing both the numerator and denominator by it. GCF = 4, and getting our simplified answer:
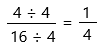
Therefore, the simplified answer is 1/4.
Write each improper fraction as a mixed number.
Question 8.
\(\frac{10}{7}\) = ____
Answer:
Conversion of the improper fraction to mixed number:
In order to convert an improper fraction to a mixed number, we need to divide the numerator by the denominator. After the division, the mixed number is formed in such a way that the quotient that is obtained becomes the whole number, the remainder becomes the new numerator and the denominator remains the same.
The above-given improper fraction: 10 / 7
step-by-step solution:
Step 1: Divide the numerator (10) by the denominator (7)
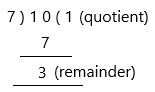
step 2: Now write the answer using the quotient (1) as the whole number and the remainder (3) as the numerator, keeping the same denominator (7). Thus, the improper fraction 10/7 is equivalent to 1 3/7 as a mixed number in its simplest form.
Therefore, the mixed number is 1 3/7.
Question 9.
\(\frac{3}{2}\) = ____
Answer:
Conversion of the improper fraction to mixed number:
In order to convert an improper fraction to a mixed number, we need to divide the numerator by the denominator. After the division, the mixed number is formed in such a way that the quotient that is obtained becomes the whole number, the remainder becomes the new numerator and the denominator remains the same.
The above-given improper fraction: 3/2
Step 1: Divide the numerator (3) by the denominator (2)
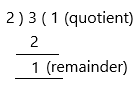
step 2: Now write the answer using the quotient (1) as the whole number and the remainder (1) as the numerator, keeping the same denominator (2). Thus, the improper fraction 3/2 is equivalent to 1 1/2 as a mixed number in its simplest form.
Therefore, the mixed number is 1 1/2.
Question 10.
\(\frac{14}{6}\) = ____
Answer:
Conversion of the improper fraction to mixed number:
In order to convert an improper fraction to a mixed number, we need to divide the numerator by the denominator. After the division, the mixed number is formed in such a way that the quotient that is obtained becomes the whole number, the remainder becomes the new numerator and the denominator remains the same.
The above-given improper fraction: 14 / 6
Step 1: Divide the numerator (14) by the denominator (6)
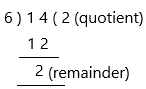
step 2: Now write the answer using the quotient (2) as the whole number and the remainder (2) as the numerator, keeping the same denominator (6). Thus, the improper fraction 14/6 is equivalent to 2 2/6 but the fraction part can still be reduced.
Dividing the fraction 26 by the GCD(2,6) = 2, we get 1/3.
so, 14/6 = 2 2/6 = 2 1/3 as a mixed number in its simplest form.
Question 11.
\(\frac{22}{4}\) = ____
Answer:
Conversion of the improper fraction to mixed number:
In order to convert an improper fraction to a mixed number, we need to divide the numerator by the denominator. After the division, the mixed number is formed in such a way that the quotient that is obtained becomes the whole number, the remainder becomes the new numerator and the denominator remains the same.
The above-given improper fraction: 14 / 6
Step 1: Divide the numerator (22) by the denominator (4)
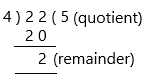
step 2: Now write the answer using the quotient (5) as the whole number and the remainder (2) as the numerator, keeping the same denominator (4). Thus, the improper fraction 22/4 is equivalent to 5 2/4 but the fraction part can still be reduced. Dividing the fraction 24 by the GCD(2,4) = 2, we get 1/2.
So, 22/4 = 5 2/4 = 5 1/2 as a mixed number in its simplest form.
Question 12.
\(\frac{30}{7}\) = ____
Answer:
Conversion of the improper fraction to mixed number:
In order to convert an improper fraction to a mixed number, we need to divide the numerator by the denominator. After the division, the mixed number is formed in such a way that the quotient that is obtained becomes the whole number, the remainder becomes the new numerator and the denominator remains the same.
Step 1: Divide the numerator (30) by the denominator (7)
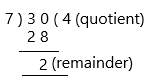
Step 2: Build your answer using the quotient (4) as the whole number and the remainder (2) as the numerator, keeping the same denominator (7). Thus, the improper fraction of 30/7 is equivalent to 4 2/7 as a mixed number in its simplest form.
Question 13.
\(\frac{41}{8}\) = ____
Answer:
Conversion of the improper fraction to mixed number:
In order to convert an improper fraction to a mixed number, we need to divide the numerator by the denominator. After the division, the mixed number is formed in such a way that the quotient that is obtained becomes the whole number, the remainder becomes the new numerator and the denominator remains the same.
Step 1: Divide the numerator (41) by the denominator (8)

Step 2: Build your answer using the quotient (5) as the whole number and the remainder (1) as the numerator, keeping the same denominator (8). Thus, the improper fraction 41/8 is equivalent to 5 1/8 as a mixed number in its simplest form.
Question 14.
A recipe for potato casserole calls for \(\frac{7}{4}\) cups of cheese. Write the fraction as a mixed number.
Answer:
The above-given improper fraction: 7/4
Step 1: Divide the numerator (7) by the denominator (4)
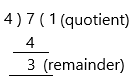
Step 2: Build your answer using the quotient (1) as the whole number and the remainder (3) as the numerator, keeping the same denominator (4). Thus, the improper fraction 7/4 is equivalent to 1 3/4 as a mixed number in its simplest form.
My Math Words
Review Vocabulary
factors greatest common factor (GCF)
least common multiple (LCM) mixed numbers multiples
Making Connections
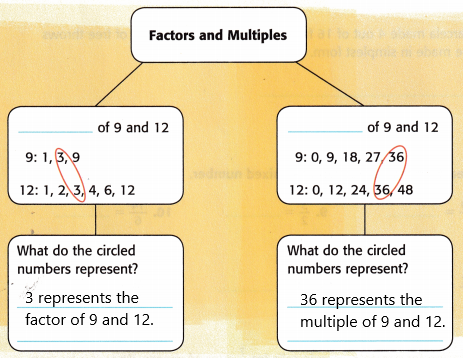
Use the review words to complete the diagram below which relates factors and multiples of the numbers 9 and 12.
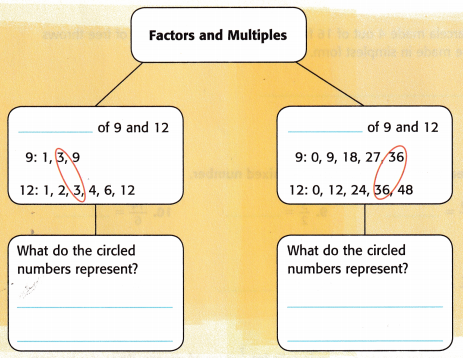
How can the greatest common factors and least common multiples help you work with fractions?
Answer:
Least common multiple:
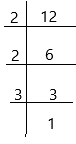
The least common multiple can be found by multiplying the highest exponent prime factors of 12 and 9. First, we will calculate the prime factors of 12 and 9.
prime factorization of 12:
Prime factorization of 9: 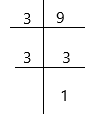
List of positive integer factors of 12 that divides 12 without a remainder: 1, 2, 3, 4, 6, 12
List of positive integer factors of 9 that divides 9 without a remainder: 1, 3, 9
by taking common prime factors GCFs of 12 and 9 are 3
The formula of LCM is LCM(a,b) = ( a × b) / GCF(a,b).
We need to calculate the greatest common factors 12 and 9 and then apply them to the LCM equation.
GCF(12,9) = 3
LCM(12,9) = ( 12 × 9) / 3
LCM(12,9) = 108 / 3
LCM(12,9) = 36
My Vocabulary Cards
Ideas for Use
- Practice your penmanship! Write this chapter’s essential question and each word in cursive.
- Use the back of the card to write or draw examples to help you answer the essential question.
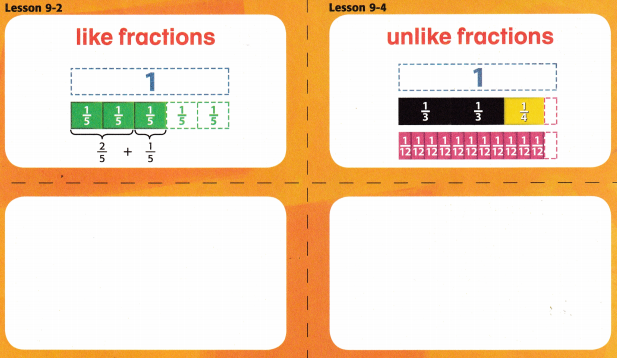
Fractions that have different denominators.
How can the prefix un- help you remember the meaning of unlike fractions?
Fractions that have the same denominator.
Like is used as an adjective in like fractions. Write a sentence using like as a verb.

My Foldable
Foldables Follow the steps on the back to make your Foldable.

Answer:

Foldables Study Organizer

For examples:
