All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 8 Lesson 8 Write Fractions as Decimals will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 8 Lesson 8 Write Fractions as Decimals
Math in My World
Example 1
The average weight of a tennis racquet is \(\frac{2}{5}\) pound. Write this weight as a decimal.
Write \(\frac{2}{5}\) as a decimal.
1. Write \(\frac{2}{5}\) as an equivalent fraction with a denominator of 10.
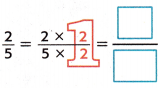
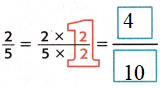
Since 5 × 2 = 10, multiply 2 × 2 to obtain 4.
2. Write the fraction with a denominator of 10 as a decimal. 2
\(\frac{2}{5}\) = ____ \(\frac{4}{10}\) means four tenths, or 0.4.
You can use a place-value chart to read the decimal.
Read the decimal. It reads four tenths
The average weight of a tennis racquet is 0.4 pound.

Example 2.
1. Write \(\frac{3}{4}\) as an equivalent fraction with a denominator of 100.
Helpful Hint
Multiplying the numerator and 8 denominator by the same number is the same as multiplying the fraction by 1. The result is an equivalent fraction.
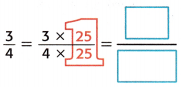
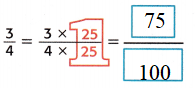
Since 4 × 25 = 100, multiply 3 × 25 to obtain 75.
2. Write the fraction with a denominator of 100 as a decimal.
\(\frac{3}{4}\) = \(\frac{75}{100}\) means seventy-five hundredths, or 0.75.
Read the decimal as seventy-five hundredths
Guided Practice
Question 1.
Write \(\frac{1}{5}\) as a decimal.
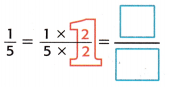
So, \(\frac{1}{5}\) = ____
Read the decimal as _____
Answer:
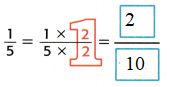
Explanation:
Since 5 × 2 = 10, multiply 1 × 2 to obtain 2.
Write the fraction with a denominator of 10 as a decimal.
\(\frac{3}{4}\) = \(\frac{75}{100}\) means seventy-five hundredths, or 0.75.
Read the decimal as seventy-five hundredths
Talk Math
Explain how to write a fraction as a decimal using equivalent fractions.

Question 2.
Write \(\frac{11}{25}\) as a decimal.
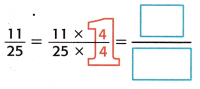
So, \(\frac{11}{25}\) = ____
Read the decimal as _____
Answer: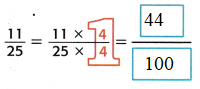
Explanation:
Since 25 × 4 = 100, multiply 11 × 4 to obtain 44.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{11}{25}\) = \(\frac{44}{100}\) means Forty four hundredths, or 0.44.
Read the decimal as Forty four hundredths
Independent Practice
Write each fraction as a decimal.
Question 3.
\(\frac{8}{10}\) = ____
Answer:
\(\frac{8}{10}\) = 0.8
Explanation:
Since it is the fraction with denominator 10 we can make it to decimal.
\(\frac{8}{10}\) = eight tenths or 0.8
Question 4.
\(\frac{1}{20}\) = ____
Answer:
\(\frac{1}{20}\) = 0.05
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20 × 5 = 100, multiply 1 × 5 to obtain 5.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{1}{20}\) = \(\frac{5}{100}\) means five hundredths, or 0.05.
Read the decimal as five hundredths
Question 5.
\(\frac{17}{20}\) = ____
Answer:
\(\frac{17}{20}\) = 0.85
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20 × 5 = 100, multiply 17 × 5 to obtain 85.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{17}{20}\) = \(\frac{85}{100}\) means eighty five hundredths, or 0.85.
Read the decimal as eighty five hundredths
Question 6.
\(\frac{4}{25}\) = ____
Answer:
\(\frac{4}{25}\) = 0.16
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4 = 100, multiply 4 × 4 to obtain 16.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{4}{25}\) = \(\frac{16}{100}\) means sixteen hundredths, or 0.16.
Read the decimal as sixteen hundredths
Question 7.
\(\frac{1}{10}\) = ____
Answer:
\(\frac{1}{10}\) = 0.1
Explanation:
Since it is the fraction with denominator 10 we can make it to decimal.
\(\frac{1}{10}\) = one tenths or 0.1
Question 8.
\(\frac{8}{25}\) = ____
Answer:
\(\frac{8}{25}\) = 0.32
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4 = 100, multiply 8 × 4 to obtain 32.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{8}{25}\) = \(\frac{32}{100}\) means thirty two hundredths, or 0.32.
Read the decimal as thirty two hundredths
Question 9.
\(\frac{14}{25}\) = ____
Answer:
\(\frac{14}{25}\) = 0.56
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4 = 100, multiply 14× 4 to obtain 56.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{14}{25}\) = \(\frac{56}{100}\) means fifty six hundredths, or 0.56.
Read the decimal as fifty six hundredths
Question 10.
\(\frac{1}{4}\) = ____
Answer:
\(\frac{1}{4}\) = 0.25
Explanation:
Find equivalent fractions with a denominator of 100.
Since 4× 25= 100, multiply 1× 25 to obtain 25.
Write the fraction with a denominator of 100 as a decimal.
So,\(\frac{1}{4}\) = \(\frac{25}{100}\) means twenty five hundredths, or 0.25.
Read the decimal as twenty five hundredths
Question 11.
\(\frac{7}{20}\) = ____
Answer:
\(\frac{7}{20}\) = 0.35
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20× 5= 100, multiply 7× 5 to obtain 35.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{7}{20}\) = \(\frac{35}{100}\) means thirty five hundredths, or 0.35.
Read the decimal as thirty five hundredths
Question 12.
\(\frac{1}{25}\) = ____
Answer:
\(\frac{1}{25}\) = 0.04
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4= 100, multiply 1× 4 to obtain 4.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{1}{25}\) = \(\frac{4}{100}\) means four hundredths, or 0.04.
Read the decimal as four hundredths
Question 13.
\(\frac{9}{10}\) = ____
Answer:
\(\frac{9}{10}\) = 0.9
Explanation:
Since it is the fraction with denominator 10 we can make it to decimal.
\(\frac{9}{10}\) = nine tenths or 0.9
Question 14.
\(\frac{9}{25}\) = ____
Answer:
\(\frac{9}{25}\) = 0.36
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4= 100, multiply 9 × 4 to obtain 36.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{9}{25}\) = \(\frac{36}{100}\) means thirty six hundredths, or 0.36.
Read the decimal as thirty six hundredths
Algebra Find each unknown.
Question 15.
\(\frac{g}{20}\) = 0.65
g = ____
Answer:
13
Explanation:
\(\frac{g}{20}\) = 0.65
Multiply all terms by the same value to eliminate fraction denominators
20 × \(\frac{g}{20}\) = 20 × 0.65
Cancel multiplied terms that are in the denominator
g = 20 × 0.65
Multiply the numbers
g = 13
Question 16.
0.7 = \(\frac{7}{w}\)
w = ____
Answer:
w = 10
Explanation:
w × 0.7 = 7
0.7w = 7
\(\frac{0.7w}{0.7}\) = \(\frac{7}{0.7}\)
w = \(\frac{7}{0.7}\)
w = 10
Question 17.
\(\frac{n}{50}\) = 0.18
n = ____
Answer:
n = 9
Multiply all terms by the same value to eliminate fraction denominators
\(\frac{n}{50}\) = 0.18
50 × \(\frac{n}{50}\) = 50 × 0.18
Cancel multiplied terms that are in the denominator
n = 50 × 0.18
Multiply the numbers
n = 9
Problem Solving
Question 18.
The smallest known female spider is \(\frac{23}{50}\) millimeter long. The smallest male spider is \(\frac{37}{100}\) millimeter long. Write each fraction as a decimal.
Answer:
\(\frac{23}{50}\) = 0.46
\(\frac{37}{100}\) = 0.46
Explanation:
Female spider is \(\frac{23}{50}\) millimeter long
Find equivalent fractions with a denominator of 100.
Since 50 × 2 = 100, multiply 23 × 2 to obtain 46.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{23}{50}\) = \(\frac{46}{100}\) means forty six hundredths, or 0.46.
Read the decimal as forty six hundredths
Smallest male spider is \(\frac{37}{100}\) millimeter long
Since it is the fraction with denominator 100 we can make it to decimal.
\(\frac{37}{100}\) = thirty seven hundredths or 0.46
Question 19.
Mathematical PRACTICE 4 Model Math Evan drank \(\frac{2}{25}\) gallon of water throughout the day. Write \(\frac{2}{25}\) as a decimal.
Answer:
\(\frac{2}{25}\) = 0.08
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4= 100, multiply 2 × 4 to obtain 8.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{2}{25}\)= \(\frac{8}{100}\) means eight hundredths, or 0.08.
Read the decimal as eight hundredths
Question 20.
At hockey practice, Savannah spent \(\frac{19}{20}\) hour practicing passing. Write \(\frac{19}{20}\) as a decimal.
Answer:
\(\frac{19}{20}\) = 0.95
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20× 5= 100, multiply 19 × 5 to obtain 95.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{19}{20}\) = \(\frac{95}{100}\) means ninety five hundredths, or 0.95.
Read the decimal as ninety five hundredths
HOT Problems
Question 21.
Mathematical PRACTICE 3 Find the Error Juliana wrote the steps below to write the fraction \(\frac{18}{25}\) as a decimal. Find her error and correct it.
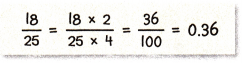
Answer:
\(\frac{18}{25}\) = 0.72
Error is Juliana should multiply 4 to numerator. She multiplied 2.
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25× 4= 100, multiply 18 × 4 to obtain 72.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{18}{25}\) = \(\frac{72}{100}\) means seventy two hundredths, or 0.72.
Read the decimal as seventy two hundredths
Question 22.
? Building on the Essential Question What is the relationship between fractions and decimals?
Answer:
Both fractions and decimals are just two ways to represent numbers.
Fractions are written in the form of p/q, where q≠0, while in decimals, the whole number part and fractional part are connected through a decimal point, for example, 0.5.
Fractions and decimals represent the relationship of part by whole.
McGraw Hill My Math Grade 5 Chapter 4 Lesson 8 My Homework Answer Key
Practice
Write each fraction as a decimal
Question 1.
\(\frac{1}{2}\) = _____
Answer:
\(\frac{1}{2}\) = 0.5
Explanation:
Find equivalent fractions with a denominator of 10.
Since 2 × 5= 10, multiply 1 × 5 to obtain 5.
Write the fraction with a denominator of 10 as a decimal.
So, \(\frac{1}{2}\) = \(\frac{5}{10}\) means five tenths, or 0.5.
Read the decimal as five tenths
Question 2.
\(\frac{11}{20}\) = _____
Answer:
\(\frac{11}{20}\) = 0.55
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20 × 5= 100, multiply 11 × 5 to obtain 55.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{11}{20}\) = \(\frac{55}{100}\) means fifty five hundredths, or 0.55.
Read the decimal as fifty five hundredths
Question 3.
\(\frac{13}{20}\) = _____
Answer:
\(\frac{13}{20}\) = 0.65
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20 × 5= 100, multiply 13 × 5 to obtain 65.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{13}{20}\) = \(\frac{65}{100}\) means sixty five hundredths, or 0.65.
Read the decimal as sixty five hundredths
Question 4.
\(\frac{6}{10}\) = _____
Answer:
\(\frac{6}{10}\) = 0.6
Explanation:
Since it is the fraction with denominator 10 we can make it to decimal.
\(\frac{6}{10}\) = six tenths or 0.6
Question 5.
\(\frac{13}{25}\) = _____
Answer:
\(\frac{13}{25}\) = 0.52
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4= 100, multiply 13 × 4 to obtain 52.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{13}{25}\) = \(\frac{52}{100}\) means fifty two hundredths, or 0.52.
Read the decimal as fifty two hundredths
Question 6.
\(\frac{14}{20}\) = _____
Answer:
\(\frac{14}{20}\) = 0.70
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20 × 5= 100, multiply 14 × 5 to obtain 70.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{14}{20}\) = \(\frac{70}{100}\) means seventy hundredths, or 0.70.
Read the decimal as seventy hundredths
Problem Solving
Question 7.
Courtney hit the bullseye \(\frac{3}{5}\) of the time when playing darts. Write \(\frac{3}{5}\) as a decimal.
Answer:
\(\frac{3}{5}\) = 0.6
Explanation:
Find equivalent fractions with a denominator of 10.
Since 5 × 2= 10, multiply 3 × 2 to obtain 6.
Write the fraction with a denominator of 10 as a decimal.
So, \(\frac{3}{5}\) = \(\frac{6}{10}\) means six tenths, or 0.6.
Read the decimal as six tenths
Question 8.
Mathematical PRACTICE 2 Use Number Sense Yesterday, it rained \(\frac{9}{20}\) inch. Write \(\frac{9}{20}\) as a decimal.
Answer:
\(\frac{9}{20}\) = 0.45
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20 × 5= 100, multiply 9 × 5 to obtain 45.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{9}{20}\) = \(\frac{45}{100}\) means forty five hundredths, or 0.45.
Read the decimal as forty five hundredths
Question 9.
Camille shaded \(\frac{12}{25}\) of a model. Write the decimal that represents the shaded portion of the model.
Answer:
\(\frac{12}{25}\) = 0.48
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4= 100, multiply 12 × 4 to obtain 48.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{12}{25}\) = \(\frac{48}{100}\) means forty eight hundredths, or 0.48.
Read the decimal as forty eight hundredths
Question 10.
Paolo built a model car that is \(\frac{7}{25}\) the size of his dad’s car. Write \(\frac{7}{25}\) as a decimal.
Answer:
\(\frac{7}{25}\) = 0.28
Explanation:
Find equivalent fractions with a denominator of 100.
Since 25 × 4= 100, multiply 7× 4 to obtain 28.
Write the fraction with a denominator of 100 as a decimal.
So,\(\frac{7}{25}\) = \(\frac{28}{100}\) means twenty eight hundredths, or 0.28.
Read the decimal as twenty eight hundredths
Question 11.
Bishon sold \(\frac{3}{20}\) of his collection of sports cards. Write \(\frac{3}{20}\) as a decimal.
Answer:
\(\frac{3}{20}\) = 0.15
Explanation:
Find equivalent fractions with a denominator of 100.
Since 20 × 5= 100, multiply 3 × 5 to obtain 15.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{3}{20}\) = \(\frac{15}{100}\) means fifteen hundredths, or 0.15.
Read the decimal as fifteen hundredths
Test Practice
Question 12.
Emilia bought \(\frac{9}{12}\) pound of sliced salami at the deli counter. Which of the following decimals did the scale show?
A. 0.25 pound
B. 0.34 pound
C. 0.7 pound
D. 0.75 pound
Answer:
D
Explanation:
The simplest form of \(\frac{9}{12}\) is \(\frac{3}{4}\)
Find equivalent fractions with a denominator of 100.
Since 4 × 25= 100, multiply 3 × 25 to obtain 75.
Write the fraction with a denominator of 100 as a decimal.
So, \(\frac{3}{4}\) = \(\frac{75}{100}\) means seventy five hundredths, or 0.75.
Read the decimal as seventy five hundredths