All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 8 Lesson 6 Compare Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 8 Lesson 6 Compare Fractions
Math in My World
Example 1
Trevor made 2 out of 3 goals and Tyler made 5 out of 6. Who made a greater fraction of goals?
1. Find the LCM of the denominators of \(\frac{2}{3}\) and \(\frac{5}{6}\).
3: 3, 6, 9, 12, 15, 18, 21, 24, 27 and 30
6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 ← The LCM of 3 and 6 is 6
2. Find equivalent fractions with a denominator of 6
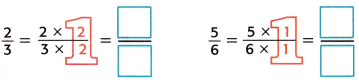
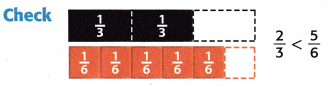
3. Compare the numerators.
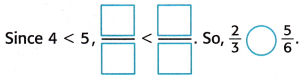
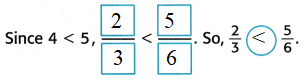
\(\frac{2}{3}\) < \(\frac{5}{6}\)
So, \(\frac{5}{6}\) made a greater fraction of goals.
Helpful Hint
Multiplying the numerator and denominator by the same number is the same as multiplying the fraction by 1. The result is an equivalent fraction.
Example 2
Compare \(\frac{3}{5}\) and \(\frac{1}{2}\) using the least common denominator.
1. Find the LCM of the denominators.
5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
2: 2, 4, 6, 8, 10, 12, 14, 16← The LCM of 2 and 5 is 10
2. Find equivalent fractions with a denominator of 10
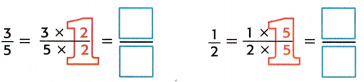
3. Compare the numerators.
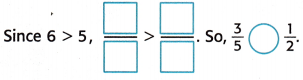
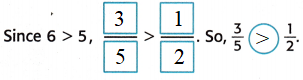
Check The models show that \(\frac{3}{5}\) > \(\frac{1}{2}\).
Guided Practice
Talk Math
Explain how the LCM and the LCD are alike. How are they different?
Answer:
The LCD and the LCM require the same math process.
Finding a common multiple of two (or more) numbers.
The only difference between LCD and LCM is that the LCD is the LCM in the denominator of a fraction. So, one could say that the least common denominators are a special case of least common multiples.
Question 1.
Compare \(\frac{1}{5}\) and \(\frac{1}{3}\) using the LCD.
5: _______
3: _______
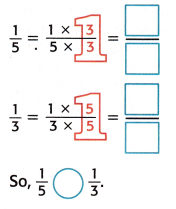
Answer:
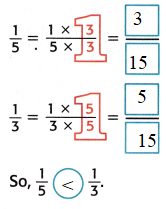
Explanation:
5 : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
3: 3, 6, 9, 12, 15, 18, 21, 24, 27
LCM of 5 and 3 is 15
\(\frac{1}{5}\) < \(\frac{1}{3}\)
Independent Practice
Mathematical PRACTICE 6 Be Precise Compare each pair of fractions by drawing models or using the LCD. Use the symbols <, >, or =.
Question 2.
\(\frac{3}{4}\) 
\(\frac{7}{8}\)
Answer:
4 : 4, 8, 12, 26, 20, 24, 28, 32, 36
8 : 8, 16, 24, 32, 40, 48, 56, 64
LCM of 4 and 8 is 8
Explanation:
Find equivalent fractions with a denominator of 8
\(\frac{6}{8}\) and \(\frac{7}{8}\)
Compare numerators 6 is less than 7 so,
\(\frac{3}{4}\) 
\(\frac{7}{8}\)
Question 3.
\(\frac{2}{3}\) \(\frac{7}{10}\)
Answer:
3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
10 : 10, 20, 30, 40, 50, 60, 70, 80, 90
LCM of 3 and 10 is 30
Explanation:
Find equivalent fractions with a denominator of 30
\(\frac{20}{30}\) and \(\frac{21}{30}\)
Compare numerators 20 is less than 21 so,
\(\frac{2}{3}\) \(\frac{7}{10}\)
Question 4.
\(\frac{2}{3}\) \(\frac{7}{12}\)
Answer:
3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
12 :12, 24, 36, 48, 60, 72, 84
LCM of 3 and 12 is 12
Explanation:
Find equivalent fractions with a denominator of 12
\(\frac{8}{12}\) and \(\frac{7}{12}\)
Compare numerators 8 is greater than 7 so,
\(\frac{2}{3}\) 
\(\frac{7}{12}\)
Question 5.
\(\frac{1}{3}\) \(\frac{5}{9}\)
Answer:
3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
9 : 9, 18, 27, 36, 45, 54, 63, 72
LCM of 3 and 9 is 9
Explanation:
Find equivalent fractions with a denominator of 9
\(\frac{3}{9}\) and \(\frac{5}{9}\)
Compare numerators 3 is less than 5 so,
\(\frac{1}{3}\) \(\frac{5}{9}\)
Question 6.
\(\frac{1}{4}\) \(\frac{1}{6}\)
Answer:
4 : 4, 8, 12, 26, 20, 24, 28, 32, 36 and 40
6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
LCM of 4 and 6 is 12
Explanation:
Find equivalent fractions with a denominator of 12
\(\frac{3}{12}\) and \(\frac{2}{12}\)
Compare numerators 3 is greater than 2 so,
\(\frac{1}{4}\) \(\frac{1}{6}\)
Question 7.
\(\frac{2}{5}\) \(\frac{6}{15}\)
Answer:
5 : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
15 : 15, 30, 45, 60, 75, 90, 105, 120
LCM of 5 and 15 is 15
Explanation:
Find equivalent fractions with a denominator of 15
\(\frac{6}{15}\) and \(\frac{6}{15}\)
Compare numerators 6 is equal to 6 so,
\(\frac{2}{5}\) 
\(\frac{6}{15}\)
Question 8.
\(\frac{2}{3}\) \(\frac{3}{4}\)
Answer:
3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
4 : 4, 8, 12, 26, 20, 24, 28, 32, 36 and 40
LCM of 3 and 4 is 12
Explanation:
Find equivalent fractions with a denominator of 12
\(\frac{8}{12}\) and \(\frac{9}{12}\)
Compare numerators 8 is less than 9 so,
\(\frac{2}{3}\) \(\frac{3}{4}\)
Question 9.
\(\frac{1}{5}\) \(\frac{3}{15}\)
Answer:
5 : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
15 : 15, 30, 45, 60, 75, 90, 105, 120
LCM of 5 and 15 is 15
Explanation:
Find equivalent fractions with a denominator of 15
\(\frac{3}{15}\) and \(\frac{3}{15}\)
Compare numerators 3 is equal to 3 so,
\(\frac{1}{5}\) \(\frac{3}{15}\)
Question 10.
\(\frac{1}{6}\) \(\frac{1}{3}\)
Answer:
6 : 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
LCM of 6 and 3 is 6
Explanation:
Find equivalent fractions with a denominator of 6
\(\frac{1}{6}\) and \(\frac{2}{6}\)
Compare numerators 1 is less than 2 so,
\(\frac{1}{6}\) \(\frac{1}{3}\)
Algebra Find each unknown in each equation that shows equivalent fractions.
Question 11.
\(\frac{3 \times m}{4 \times 5}\) = \(\frac{P}{20}\)
m = ____
P = _____
Answer:
\(\frac{3 \times m}{4 \times 5}\) = \(\frac{P}{20}\)
3 × m × 20 = 4 × 5 × P
60m = 20P
3m = P
m = P/3
Question 12.
\(\frac{7 \times g}{8 \times k}\) = \(\frac{21}{24}\)
g = ____
k = _____
Answer:
\(\frac{7 \times g}{8 \times k}\) = \(\frac{21}{24}\)
\(\frac{7 \times g}{8 \times k}\) = \(\frac{7 × 3}{8 × 3}\)
g = 3
k = 3
Question 13.
\(\frac{5}{6}\) = \(\frac{b}{48}\)
b = _____
Answer:
40
Multiply all terms by the same value to eliminate fraction denominators
\(\frac{5}{6}\) = \(\frac{b}{48}\)
48 × \(\frac{5}{6}\) = 48 × \(\frac{b}{48}\)
Cancel multiplied terms that are in the denominator
8 × 5 = b
Multiply the numbers
b = 40
Problem Solving
Question 14.
The amounts of water four runners drank are shown at the right. Who drank the most?
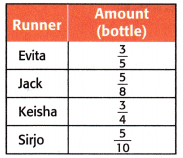
Answer:
5 : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
8 : 8, 16, 24, 32, 40, 48, 56, 64
4 : 4, 8, 12, 26, 20, 24, 28, 32, 36 and 40
10 : 10, 20, 30, 40, 50, 60, 70, 80, 90
LCM of 5, 8, 4, 10 is 40
Explanation:
Find equivalent fractions with a denominator of 40
\(\frac{24}{40}\) , \(\frac{25}{40}\), \(\frac{30}{40}\), \(\frac{20}{40}\)
Comparing numerators,30 is greater than all so,
Keisha drank the most that is \(\frac{3}{4}\)
Question 15.
Mathematical PRACTICE 6 Be Precise A recipe calls for \(\frac{5}{8}\) cup of brown sugar and \(\frac{2}{3}\) cup of flour. Which ingredient has the greater amount?
Answer:
8 : 8, 16, 24, 32, 40, 48, 56, 64
3: 3, 6, 9, 12, 15, 18, 21, 24, 27
LCM of 8 and 3 is 24
Explanation:
Find equivalent fractions with a denominator of 24
\(\frac{15}{24}\) and \(\frac{16}{24}\)
Comparing numerators,15 is less than 16 so,
\(\frac{2}{3}\) cup of flour has the greater amount.
Question 16.
A trail mix has \(\frac{1}{2}\) cup of raisins and \(\frac{2}{3}\) cup of peanuts. Which ingredient has the greater amount?
Answer:
2 : 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
3: 3, 6, 9, 12, 15, 18, 21, 24, 27 and 30.
LCM of 2 and 3 is 6
Explanation:
Find equivalent fractions with a denominator of 6
\(\frac{3}{6}\) and \(\frac{4}{6}\)
Comparing numerators,3 is less than 4 so,
\(\frac{2}{3}\) cup of peanuts has the greater amount
HOT Problems
Question 17.
Mathematical PRACTICE 2 Use Number Sense Explain why multiplying the numerator and denominator of a fraction by the same number results in an equivalent fraction.
Answer:
If you multiply both the numerator and denominator of a fraction by the same non-zero number, the fraction remains unchanged in value.
Therefore, equivalent fractions can be created by multiplying (or dividing) the numerator and denominator by the same number.
This number is referred to as a multiplier.
Question 18.
? Building on the Essential Question What is one way to compare fractions with unlike denominators?
Answer:
We can compare fractions with unlike denominators by finding the least common denominator, or the smallest multiple the denominators share.
Then we make equivalent fractions, or fractions that represent the same part of the whole.
McGraw Hill My Math Grade 5 Chapter 4 Lesson 6 My Homework Answer Key
Practice
Compare each pair of fractions by drawing models or using the LCD. Use the symbols <, >, or =.
Question 1.
\(\frac{3}{4}\) 
\(\frac{7}{8}\)
Answer:
4: 4, 8, 12, 26, 20, 24, 28, 32, 36 and 40.
8 : 8, 16, 24, 32, 40, 48, 56, 64
LCM of 4 and 8 is 8
Explanation:
Find equivalent fractions with a denominator of 8
\(\frac{6}{8}\) and \(\frac{7}{8}\)
Comparing numerators,6 is less than 7 so,
\(\frac{3}{4}\) \(\frac{7}{8}\)
Question 2.
\(\frac{1}{3}\) \(\frac{3}{9}\)
Answer:
3: 3, 6, 9, 12, 15, 18, 21, 24, 27
9 : 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
LCM of 3 and 9 is 9
Explanation:
Find equivalent fractions with a denominator of 9
\(\frac{3}{9}\) and \(\frac{3}{9}\)
Comparing numerators,3 is equal to 3 so,
\(\frac{1}{3}\) \(\frac{3}{9}\)
Question 3.
\(\frac{3}{4}\) \(\frac{2}{3}\)
Answer:
4 : 4, 8, 12, 26, 20, 24, 28, 32, 36 and 40
3: 3, 6, 9, 12, 15, 18, 21, 24, 27
LCM of 4 and 3 is 12
Explanation:
Find equivalent fractions with a denominator of 12
\(\frac{9}{12}\) and \(\frac{8}{12}\)
Comparing numerators,9 is greater than 8 so,
\(\frac{3}{4}\) \(\frac{2}{3}\)
Problem Solving
Question 4.
A survey showed that \(\frac{7}{15}\) of a class liked soccer and \(\frac{2}{5}\) liked baseball. Which sport was liked less?
Answer:
15 : 15, 30, 45, 60, 75, 90, 105, 120
5 : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
LCM of 15 and 5 is 15
Explanation:
Find equivalent fractions with a denominator of 15
\(\frac{7}{15}\) and \(\frac{6}{15}\)
Comparing numerators,7 is greater than 6 so,
\(\frac{2}{5}\) was liked less
Question 5.
The fifth graders were given sandwiches for lunch during their field trip. Nathan ate \(\frac{5}{6}\) of his sandwich, Leroy ate \(\frac{7}{8}\) of his sandwich, and Sofia ate \(\frac{5}{8}\) of her sandwich. Who ate the greatest amount of their sandwich?
Answer:
6 : 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
8 : 8, 16, 24, 32, 40, 48, 56, 64
LCM of 6, 8, 8 is 24
Explanation:
Find equivalent fractions with a denominator of 24
\(\frac{20}{24}\), \(\frac{21}{24}\), \(\frac{15}{24}\)
Comparing numerators, 21 is greater than 20 and 15 so,
Leroy ate \(\frac{7}{8}\) the greatest amount of sandwich.
Question 6.
Mathematical PRACTICE 2 Use Symbols Replace 
with a number to make 
a true statement.
Answer:
7
Explanation:
4 : 4, 8, 12, 26, 20, 24, 28, 32, 36 and 40
24 : 24, 48, 72, 96, 120
LCM of 4 and 24 is 24
Explanation:
Find equivalent fractions with a denominator of 24
\(\frac{7}{24}\) and \(\frac{6}{24}\)
Comparing numerators, 7 is greater than 6 so,
The unknown value is 7 to make that statement true.
Vocabulary Check
Question 7.
Fill in the blank with the correct word to complete the sentence. The least common denominator (LCD) is the least common multiple of the ____ of the fractions.
Answer:
Denominator
Explanation:
The least common denominator (LCD) is the least common multiple of the denominator of the fractions.
Test Practice
Question 8.
Eighteen out of 24 of Emil’s CDs are country music. Five out of 8 of Imani’s CDs are country music. Which is a true statement?
A. Half of each CD collection consists of country music.
B. Less than half of each CD collection consists of country music.
C. Emil has a greater fraction of country music than Imani.
D. Imani has a greater fraction of country music than Emil.
Answer:
C
Explanation:
24 : 24, 48, 72, 96, 120
8 : 8, 16, 24, 32, 40, 48, 56, 64
LCM of 24 and 8 is 24
Explanation:
Find equivalent fractions with a denominator of 24
\(\frac{18}{24}\) and \(\frac{15}{24}\)
Comparing numerators, 18 is greater than 15 so,
Emil has a greater fraction of country music than Imani.