All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 6 Lesson 3 Multiply Decimals by Whole Numbers will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 6 Lesson 3 Multiply Decimals by Whole Numbers
Math in My World
Example 1
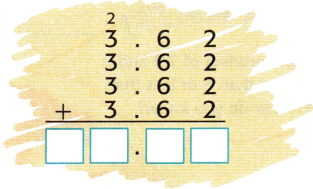
Find the area of a rectangular board that is 4 feet by 3.62 feet.

One Way:
Use repeated addition.
4 × 3.62 means __________ + ___________ + ___________ + _____________
Helpful Hint
The area of a rectangle is found by multiplying the length by the width.
Another Way:
Multiply as with whole numbers. Then count decimal places.

Check: The answer is the same whether you use repeated addition or multiplication. So, the answer is reasonable.
Answer:
14.48 square feet.
Explanation:
The area of a rectangular board that is 4 feet by 3.62 feet.
The area of a rectangular = length x width
4 × 3.62 means= 3.62 + 3.62 + 3.62 + 3.62
A= 14.48 square feet.
Another Way:
Multiply as with whole numbers. Then count decimal places.
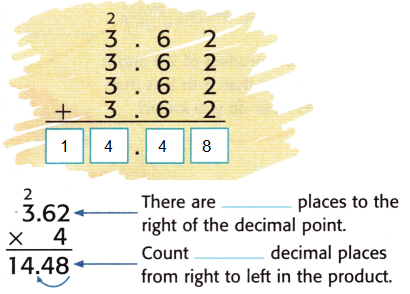
Check: The answer is the same whether you use repeated addition or multiplication. So, the answer is reasonable.
Example 2
Find 3 × 0.96.
Estimate 3 × 1 = _____________
1. Multiply as with whole numbers.
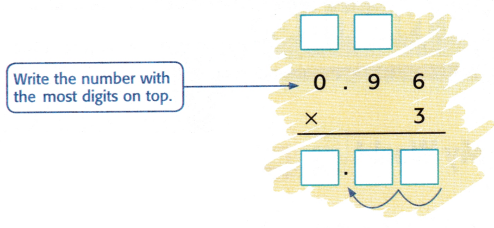
2. Count the decimal places. There are 2 places to the right of the decimal point in 0.96. So, count 2 places from right to left in the product.
So, 3 × 0.96 = ____________.
Check The product, ___________, is close to the estimate, ____________.
The answer is reasonable.
Answer:
3 x 0.96 = 2.88
Estimate: 3
Explanation:
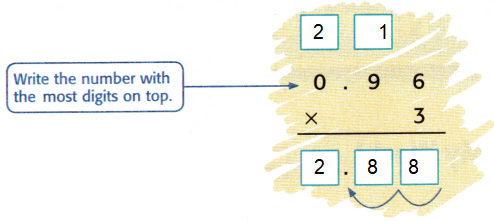
Count the decimal places.
There are 2 places to the right of the decimal point in 0.96.
So, count 2 places from right to left in the product.
So, 3 × 0.96 = 2.88.
Check The product 2.88 is close to the estimate 3.
So, the answer is reasonable.
Talk Math
Is the product of 2.8 and 2 greater than 6 or less than 6? How do you know?

Answer:
2 less than 6.
Explanation:
3 × 0.96 = 2.88.
The product 2.88 is close to the estimate 3.
2 less than 6.
Guided Practice
Multiply. Check for reasonableness.
Question 1.
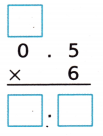
Answer:
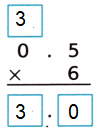
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 0.5.
So, count one place from right to left in the product.
So, 6 × 0.5 = 3.
Check The product 3.0 is close to the estimate 3.
So, the answer is reasonable.
Question 2.
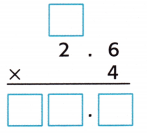
Answer:
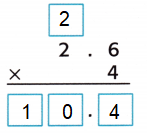
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 2.6.
So, count one place from right to left in the product.
So, 4 × 2.6 = 10.4.
Check The product 10.4 is close to the estimate 10.
So, the answer is reasonable.
Independent Practice
Multiply. Check for reasonableness.
Question 3.
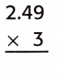
Answer:
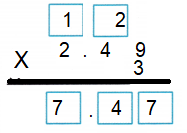
Explanation:
Count the decimal places.
There are two places to the right of the decimal point in 2.49.
So, count two places from right to left in the product.
So, 3 × 2.49 = 7.47.
So, the answer is reasonable.
Question 4.
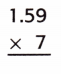
Answer:
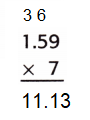
Explanation:
Count the decimal places.
There are two places to the right of the decimal point in 1.59.
So, count two places from right to left in the product.
So, 7 × 1.59 = 11.13.
So, the answer is reasonable.
Question 5.
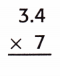
Answer:
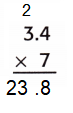
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 3.4.
So, count one place from right to left in the product.
So, 7 × 3.4 = 23.8.
So, the answer is reasonable.
Question 6.
2 × 1.3 = __________
Answer:
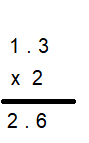
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 1.3.
So, count one place from right to left in the product.
So, 2 × 1.3 = 2.6.
So, the answer is reasonable.
Question 7.
3 × 0.5 = ___________
Answer:
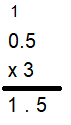
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 0.5.
So, count one place from right to left in the product.
So, 3 × 0.5 = 1.5.
So, the answer is reasonable.
Question 8.
1.8 × 9 = ____________
Answer:
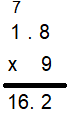
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 1.8.
So, count one place from right to left in the product.
So, 9 × 1.8 = 16.2.
So, the answer is reasonable.
Question 9.
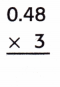
Answer:
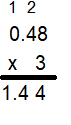
Explanation:
Count the decimal places.
There are two places to the right of the decimal point in 0.48.
So, count two places from right to left in the product.
So, 7 × 0.48 = 1.44.
So, the answer is reasonable.
Question 10.
![]()
Answer:
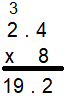
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 2.4.
So, count one place from right to left in the product.
So, 8 × 2.4 = 19.2.
The answer is reasonable.
Question 11.
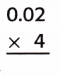
Answer:
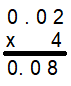
Explanation:
Count the decimal places.
There are two places to the right of the decimal point in 0.02.
So, count two places from right to left in the product.
So, 4 × 0.02 = 0.08.
So, the answer is reasonable.
Question 12.
0.66 × 5 = _____________
Answer:
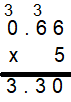
Explanation:
Count the decimal places.
There are two places to the right of the decimal point in 0.66.
So, count two places from right to left in the product.
So, 5 × 0.66 = 3.3.
So, the answer is reasonable.
Question 13.
67 × 4.3 = _____________
Answer:
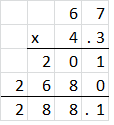
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 4.3.
So, count one place from right to left in the product.
So, 67 × 4.3 = 288.1.
So, the answer is reasonable.
Question 14.
52 × 2.1 = _____________
Answer:
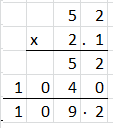
Explanation:
Count the decimal places.
There is one place to the right of the decimal point in 2.1.
So, count one place from right to left in the product.
So, 52 × 2.1 = 109.2.
So, the answer is reasonable.
Algebra Find each unknown.
Question 15.
0.8 × 9 = h
h = ___________
Answer:
7.2
Explanation:
0.8 × 9 = h
h = 7.2
Count the decimal places.
There are 1 place to the right of the decimal point in 0.8.
So, count one place from right to left in the product.
Question 16.
6 × 0.05 = x
x = ____________
Answer:
0.3
Explanation:
6 × 0.05 = x
x = 0.3
Ignore the decimals, then multiply with whole numbers.
6 x 5 = 30
Count the decimal places.
There are two places to the right of the decimal point in 0.66.
So, count two places from right to left in the product.
Question 17.
1.48 × 7 = m
m = ___________
Answer:
10.36
Explanation:
1.48 × 7 = m
m = 10.36
Ignore the decimals, then multiply with whole numbers.
148 x 7 = 1036
Count the decimal places.
There are two places to the right of the decimal point in 10.36.
So, count two places from right to left in the product.
Problem Solving

Question 18.
Mr. Thomas’ car can travel 17.6 miles per gallon of gas. If his gas tank holds 11 gallons, how far can he travel on a full tank of gas?
Answer:
193.6 miles.
Explanation:
Mr. Thomas’ car can travel 17.6 miles per gallon of gas.
If his gas tank holds 11 gallons,
Total distance he travel on a full tank of gas,
17.6 x 11 = 193.6 miles.
Question 19.
Tom and Sonia both mowed lawns last week. Tom mowed five lawns and charged $10.75 per lawn. Sonia mowed four lawns but charged $2.25 more per lawn than Tom. Who made the most money?
Answer:
Tom made the most money.
Explanation:
Tom moved five lawns and charged $10.75 per lawn.
$10.75 x 5 = $53.75
Sonia moved four lawns but charged $2.25 more per lawn than Tom.
$10.75 + $2.25 = $13
$13 x 4 = $52
compare both the lawns charged by both Tom and Sonia,
Tom made the most most.
HOT Problems
Question 20.
Mathematical PRACTICE Plan Your Solution Write a multiplication problem in which the product has two decimal places.
Answer:
Evan worked five days and earns $10.75 per day. Sonia worked four days but earned $2.25 more per day than Evan. Who earned more?
Explanation:
Evan worked five days and earned $10.75 per day.
$10.75 x 5 = $53.75
Sonia worked four days but charged $2.25 more per day than Evan.
$10.75 + $2.25 = $13
$13 x 4 = $52
So, Evan earned more than Sonia.
Question 21.
Mathematical PRACTICE Use Number Sense Place the decimal point in the answer below to make it correct. Explain your reasoning.
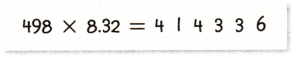
Answer:
4143.36
Explanation:
498 x 8.32 = 4143.36
Count the decimal places.
There are two places to the right of the decimal point in 8.32.
So, count two places from right to left in the product.
Question 22.
building on the Essential Question How is multiplying a decimal by a whole number similar to and different from multiplying two whole numbers?
Answer:
The only difference between multiplying whole numbers and multiplying decimals is that we have the added step of moving the decimal point after performing the multiplication when multiplying decimals.
Explanation:
For example:
48 x 3 = 144
When we multiply the whole number with the other whole number,
the product is also whole number.
4.8 x 3 = 14.4
multiplying decimals is that we have the added step of moving the decimal point after performing the multiplication when multiplying decimals.
McGraw Hill My Math Grade 5 Chapter 6 Lesson 3 My Homework Answer Key
Practice
Multiply. Check for reasonableness.
Question 1.
![]()
Answer:
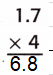
Explanation:
Multiplication is a repeated division.
1.7 + 1.7 + 1.7 + 1.7 = 6.8
Question 2.
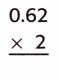
Answer:
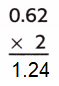
Explanation:
Multiplication is a repeated division.
0.62 + 0.62 = 1.24
Question 3.
![]()
Answer:
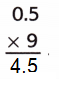
Explanation:
Multiplication is a repeated division.
0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 = 4.5
Question 4.
3.6 × 8 = ____________
Answer:
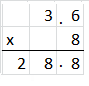
Explanation:
Multiplication is a repeated division.
3.6 + 3.6 +3.6 + 3.6 + 3.6 + 3.6 + 3.6 + 3.6 = 28.8
Question 5.
5.1 × 7 = ____________
Answer:
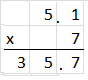
Explanation:
Multiplication is a repeated division.
5.1 + 5.1 + 5.1 + 5.1 + 5.1 + 5.1 + 5.1 = 35.7
Question 6.
4 × 2.3 = ____________
Answer:
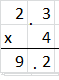
Explanation:
Multiplication is a repeated division.
2.3 + 2.3 + 2.3 + 2.3 = 9.2
Algebra Find each unknown.
Question 7.
2 × 0.33 = p
p = __________
Answer:
Explanation:
2 × 0.33 = p
p = 0.66
Ignore the decimals, then multiply with whole numbers.
2 x 33 = 66
Count the decimal places.
There are two places to the right of the decimal point in 0.33.
So, count two places from right to left in the product.
2 × 0.33 = 0.66
Question 8.
5 × 2.4 = n
n = ____________
Answer:
12
Explanation:
5 × 2.4 = n
n = 12
Ignore the decimals, then multiply with whole numbers.
5 x 24 = 12
Count the decimal places.
There is one place to the right of the decimal point in 2.4.
So, count one place from right to left in the product.
5 × 2.4 = 12
Question 9.
7 × 8.1 = s
s = _____________
Answer:
56.7
Explanation:
7 × 8.1 = s
s = 56.7
Ignore the decimals, then multiply with whole numbers.
7 x 81 = 567
Count the decimal places.
There is one place to the right of the decimal point in 8.1.
So, count one place from right to left in the product.
7 × 8.1 = 56.7
Problem Solving
Question 10.
Justin bought 9 packs of trading cards. Each pack of cards costs $3.27. What was the total cost for all 9 packs?
Answer:
$29.43
Explanation:
Justin bought 9 packs of trading cards.
Each pack of cards costs $3.27.
The total cost for all 9 packs = 9 x $3.27 = $29.43
As, multiplication is a repeated addition.
$3.27 + $3.27 + $3.27 + $3.27 + $3.27 + $3.27 + $3.27 + $3.27 + $3.27 = $29.43
Question 11.
Richard paints a picture on a rectangular canvas that is 3 feet by 2.64 feet. What is the area of Richard’s painting?
Answer:
7.92 square feet.
Explanation:
Area of rectangle = length x width
Richard paints a picture on a rectangular canvas that is 3 feet by 2.64 feet.
A = 3 x 2.64 = 7.92 square feet.
Question 12.
Mathematical PRACTICE Explain to a Friend Taylor wants to buy a bicycle that costs $48.75. She works for her mom after school to earn the money. If Taylor is paid $4.50 per hour, will she be able to buy the bicycle after working 9 hours? Explain to a friend.
Answer:
No, she can’t buy still she need $8.25.
Explanation:
Taylor wants to buy a bicycle that costs $48.75.
If Taylor is paid $4.50 per hour,
she will be able to buy the bicycle after working 9 hours,
9 x $4.50 = $40.5
Actual cost of bicycle is $48.75, but she has only $40.5.
still she need $48.75 – $40.5 = $8.25
Question 13.
Janita practices on the track field 1.5 hours each day before a track meet. If there are 6 days until the track meet, how many hours will Janita practice?

Answer:
9 hours.
Explanation:
Janita practices on the track field 1.5 hours each day before a track meet.
If there are 6 days until the track meet,
Number of hours will Janita practice 1.5 x 6 = 9hours.
Test Practice
Question 14.
Kent buys a pen that costs $1.21. How much will 4 pens?
(A) $3.63
(B) $3.84
(C) $4.21
(D) $4.84
Answer:
Option(D)
Explanation:
Kent buys a pen that costs $1.21.
Cost of 4 pens = $1.21 x 4 = $4.84