All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 2 Lesson 2 Prime Factorization Patterns will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 2 Lesson 2 Prime Factorization Patterns
Build It
You can make a pattern using paper and a hole punch. By folding the paper, hole punching it, and counting the holes, you can discover a pattern.

Question 1.
Fold a piece of paper in half and make one hole punch. Open the paper.
How many holes are in the paper? ____
Find the prime factorization for the number of holes. ____
Answer:
2 holes and the prime factorization for the number of holes are 2 × 1
Explanation:
There are 2 holes in the paper after making one hole punch.
The prime factorization for the number of holes are 2 × 1
Question 2.
Fold another piece of paper in half twice. Make one hole punch.
Unfold the paper. How many holes are in the paper? ____
What is the prime factorization for the number of holes? ____ × ____

Answer:
Number of holes = 4
Prime factorization = 2 × 2
Explanation:
The number of holes in the paper is 4.
The prime factorization for the number of holes are 2 × 2 for 4.
Question 3.
Complete the table for one, two, and three folds.
Answer:
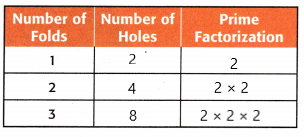
Explanation:
I have completed the given table for one, two, and three folds that is shown in the above table.
Question 4.
What pattern do you notice between the number of factors in each prime factorization and the number of folds?
Answer:
The pattern we noticed is the multiplication of even numbers.
Explanation:
The pattern between the number of factors in each prime factorization is the multiplication of even numbers.
For one fold we will get 2 number of holes
2 folds 2 × 2 = 4 number of holes.
Question 5.
Using the pattern you found in Step 4, complete the table for four and five folds.
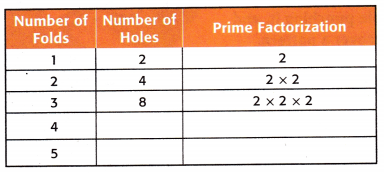
Answer:
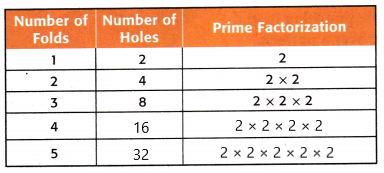
Explanation:
By using the pattern we have found in step 4 we have completed the table for four and five folds. The figure is shown above.
Talk about it
Question 1.
Which prime number did you record in each prime factorization?
Answer:
The prime number did you record in each prime factorization is 2.
Question 2.
How many holes will you make if you fold the paper eight times? Write the prime factorization of that number.
Answer:
256 and the prime factorization of that number is 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
Explanation:
The number of holes that makes it if you fold the paper eight times is 256.
The prime factorization of that number is 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
Question 3.
Mathematical PRACTICE 1 Make Sense of Problems How can you check that you have the correct prime factorization?

Answer:
A composite number is written as a multiplication of all the prime factors we can have the prime factorization of the number.
Practice It
Question 4.
Use paper and a hole punch to complete the table below. Start by folding a piece of paper in half and making 3 holes. Use a new piece of paper each time you increase the number of folds.
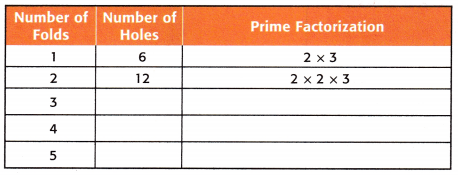
Answer:
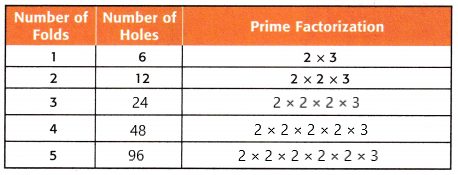
Explanation:
we have folded a piece of paper in half and made 3 holes then the prime factorization of 3 is 3 × 1
Next, the paper was folded into one and made into 6 holes then the prime factorization of 6 is 2 × 3
The above pattern repeats 5 folds.
The folds and the number of holes are shown in the above figure.
Find a pattern to complete the tables in Exercises 5—7.
Question 5.
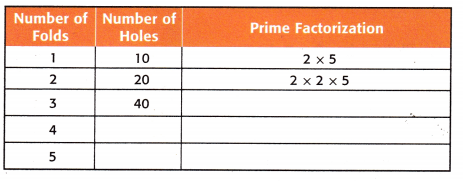
Answer:
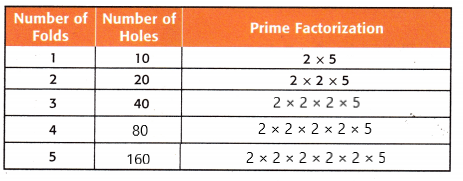
Explanation:
In the given figure the pattern follows the multiples of 10.
The prime factorization and the number of holes were shown in the above figure.
Question 6.
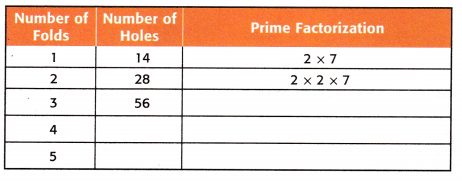
Answer:
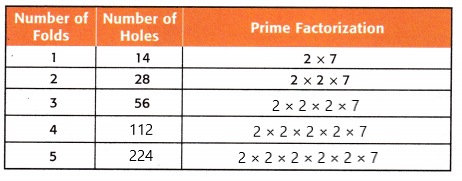
Explanation:
The prime factorization and the number of holes were shown in the above figure.
Here the pattern is multiples of 14.
Question 7.
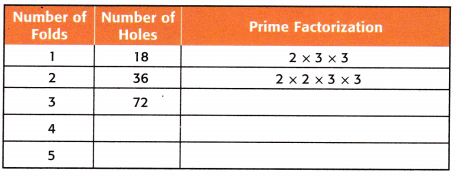
Answer:
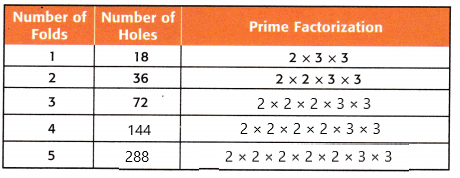
Explanation:
The prime factorization and the number of holes were shown in the above figure.
Here the pattern is multiples of 18.
Apply It
Use the information below to solve Exercises 8—11. There is one skin cell used in a science lab. Each day,
the skin cell will split into two cells. The next day the cell then splits into two cells again.
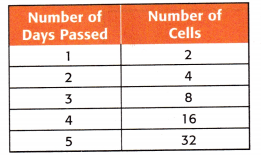
Question 8.
After several splits, there are 64 cells. How many have passed?
Answer:
6
Explanation:
The number of days passed is 6 for 64 cells.
5 days the number of cells is 32
In 6 days the number of cells is 64.
Question 9.
How many skin cells will there be after 8 days have passed?
Answer:
There will be 256 cells after 8 days have passed.
Explanation:
for 5 days the number of cells is 32
for 6 days the number of cells is 64
for 7 days the number of cells is 128
for 8 days the number of cells is 256.
Question 10.
How many days would need to pass before there were over 2,000 cells?
Answer:
The number of days would need to pass before there were over 2000 cells are 11 days.
Explanation:
Given for 8 days the number of cells is 256.
for 9 days the number of cells is 512.
for 10 days the number of cells is 1024.
for 11 days the number of cells is 2048.
Approximately number of days would need to pass before there were over 2000 cells are 11 days.
Question 11.
Mathematical PRACTICE 1 Make a Plan After 15 days, there were 32,768 cells. After how many days were there 16,384 cells?
Answer:
14 days were there 16,384 cells.
Explanation:
Given for 8 days the number of cells is 256.
for 9 days the number of cells is 512.
for 10 days the number of cells is 1024.
for 11 days the number of cells is 2048.
for 12 days the number of cells is 4096.
for 13 days the number of cells is 8192.
for 14 days the number of cells is 16,384.
Write About Ìt
Question 12.
How can I use patterns to describe relationships?
Answer:
It is a sequence that tells you how to process numbers to get an answer.
McGraw Hill My Math Grade 5 Chapter 2 Lesson 2 My Homework Answer Key
Practice
Question 1.
Complete the table for Figures 4 and 5 if the above pattern continues.

Answer:
Problem Solving
Question 2.
A population of rabbits triples every month. The population starts with two rabbits. How many rabbits are there after three months?

Answer:
54 rabbits are there after three months.
Explanation:
A population of rabbits triples every month
2 × 3 = 6
6 × 3 = 18
18 × 3 = 54
Question 3.
Three friends each create 4 bags of starter bread dough. After ten days, each of those four bags is then divided into four more bags of dough. How many days pass before 192 bags of dough are created?
Answer:
After 20 days.
Explanation:
Each of the friends has made 4 bags of dough.
This gives you 12 bags at the outset.
After 10 days all 12 bags are made into 4 × 12 = 48 bags
After 20 days the 48 bags are made into 48 × 4 = 192 bags.
Question 4.
Sam sent an E-mail to 3 friends on Monday. Each of the friends then sent an E-mail to 3 friends on Tuesday. On Wednesday, each of those friends then sent an E-mail to 3 friends. Write the prime factorization of the number of E-mails that were sent on Wednesday.
Answer:
The prime factorization of the number of E-mails that were sent on Wednesday is 21.
Explanation:
Sam sent 3 friends an email on Monday and each friend sent an email to 3 friends on Tuesday
Total of 3 + (3 × 3) = 12 emails were sent by Tuesday.
The prime factorization of the number of E-mails that were sent on Wednesday.
3 + (3 × 3) + (3 × 3)
3 + 9 + 9
21
The prime factorization is 21 = 3 × 7
Question 5.
Mathematical PRACTICE 8 Look for a Pattern Annie opened a savings account and deposited $10. If the balance in her account doubles each month, what is the account balance after 4 months?
Answer:
$160.
Explanation:
10 × 2 =20
20 × 2 = 40
40 × 2 = 80
80 × 2 =160
Therefore $160 would be in her account.
Question 6.
Elyse folded a piece of paper in half 3 times. She then punched 3 holes in the paper. How many holes are in the paper when she unfolds it?
Answer:
24 holes.
Explanation:
Elyse folded a piece of paper in one half then the surfaces of the paper will become 2.
The surfaces formed again will be 2 × 2 = 4
Then the paper is folded again for the third time then the surfaces become 2 × 2 × 2 = 8
Elyse punched a hole in the folded paper so the total holes will be 8
If we punch 3 holes then the total holes in unfolded paper will be 8 × 3 = 24 holes.
Therefore, the holes formed when the paper is unfolded are 24 holes.