All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 12 Lesson 6 Build Three-Dimensional Figures will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 12 Lesson 6 Build Three-Dimensional Figures
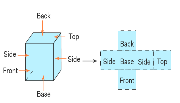
A three-dimensional figure has length, width, and height A net is a two-dimensional pattern of a three-dimensional figure. You can use a net to build a three-dimensional figure.

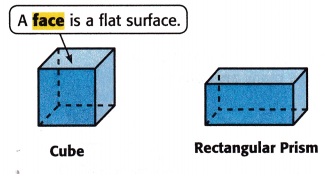
A cube is a three-dimensional figure with six faces that are congruent squares. Congruent figures have the same size and shape.
A rectangular prism is a three-dimensional figure with six rectangular faces. Opposite faces are parallel and congruent.
Build It
1. Copy the net shown onto grid paper.
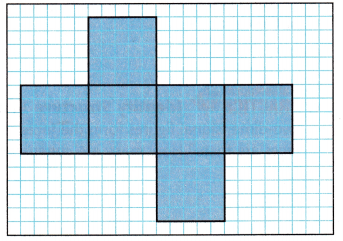
2. Cut out the net. Fold along the lines to form a three-dimensional figure. What figure did you form?
Answer: cube
Explanation:
Nets of a cube:
– A geometry net is a two-dimensional shape that can be folded to form a 3-dimensional figure.
– A net is a pattern made when the surface of a three-dimensional figure is folded such that it shows each face of the figure.
The six cubes form the faces that join the bottom to the top. As these begin to fold up in the fourth dimension, we see their shadows become distorted in three dimensions (as one face of the cubes moves closer to the light source, its shadow gets larger). Eventually, the faces of the cubes come together and are joined, just as the edges of the squares that form a cube are glued when they are folded together.
Try It
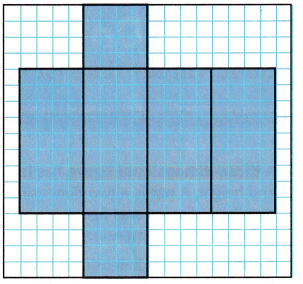
1. Copy the net shown onto grid paper.
2. Cut out the net Fold along the lines to form a three-dimensional figure. What figure did you form?
How are the two figures you just built alike?
How are the two figures you just built differently?
Answer: rectangular prism
Explanation:
The above-given three-dimensional figure forms a rectangular prism.
– The net of any prism is its surface area. It shows when we open the prism in a plane; then all its sides could be visible at the same time. If we calculate the individual area of all its sides using the net, we will get the total surface area.
– A rectangular prism has 6 faces, 12 edges and 8 vertices
– The top and base of the rectangular prism are always a rectangle
– Like a cuboid, it also has three dimensions, i.e., length width and height
– Pairs of opposite faces are identical or congruent
* How are the two figures you just built alike?
Answer: They each have six faces. The faces meet at right angles.
* How are the two figures you just built differently?
Answer: The first figure has faces that are all congruent.
Talk About It
Question 1.
In the first activity, what two-dimensional figure forms the faces of the figure? How many faces are there? How many are congruent?
Answer:
The square (two-dimensional figure) forms the faces of the cube.
– It has 6 square faces.
– The 6 faces are congruent.
– Since the faces are square in shape, the sides of a cube have equal dimensions i.e., L = B = H.
Question 2.
Identify the length, width, and height of the cube you formed in the first activity.
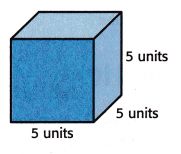
Answer:
The above-given units:
length = 5 units; width = 5 units; height = 5 units.
– Volume is the quantity of space enclosed within a three-dimensional closed surface. Volume is often measured numerically using the SI unit, the cubic metre. So, the volume of a cube = S^3.
Question 3.
What do you notice about the length, width, and height of the cube?
Answer:
– They are congruent.
– Since the faces are square in shape, the sides of a cube have equal dimensions i.e., L = B = H.
Question 4.
Mathematical PRACTICE Identify Structure In the second activity, what two-dimensional figures form the faces of the figure? How many faces are there? How many are congruent?
Answer:
– In the second activity, the two-dimensional figures are rectangular and square.
– A rectangular prism has 6 faces including bases.
– The four rectangles are congruent and 2 squares are congruent. (Pairs of opposite faces are identical and congruent).
Practice It
For Exercises 5 and 6, refer to the grid at the right.
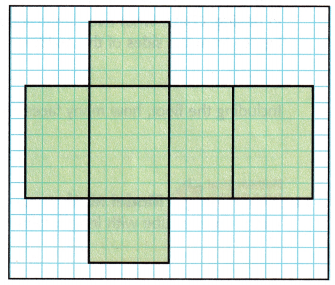
Question 5.
Copy the net onto grid paper. Cut out the net and fold along the lines to form a three-dimensional figure. What figure did you form?
Answer: rectangular prism
Explanation:
The above-given three-dimensional figure forms a rectangular prism.
– The net of any prism is its surface area. It shows when we open the prism in a plane; then all its sides could be visible at the same time. If we calculate the individual area of all its sides using the net, we will get the total surface area.
* A prism with rectangular bases is called a rectangular prism.
Question 6.
What two-dimensional figure forms the faces of the figure? How many faces are there? Describe the congruent faces.
Answer:
– Rectangles form the faces of the figure.
– A rectangular prism is a three-dimensional shape, that has six faces (two at the top and bottom and four lateral faces). All the faces of the prism are rectangular in shape. Hence, there are three pairs of identical faces here.
For Exercises 7-9, refer to the grid at the right.
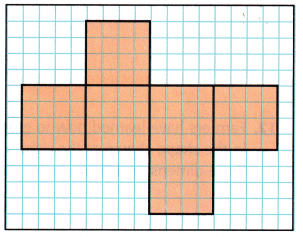
Question 7.
Copy the net onto grid paper. Cut out the net and fold along the lines to form a three-dimensional figure. What figure did you form?
Answer: cube
Explanation:
Nets of a cube:
– A geometry net is a two-dimensional shape that can be folded to form a 3-dimensional figure.
– A net is a pattern made when the surface of a three-dimensional figure is folded such that it shows each face of the figure.
Question 8.
What two-dimensional figure forms the faces of the figure?
__________________
How many faces are there?
__________________
Describe the congruent faces.
__________________
Answer:
The square (two-dimensional figure) forms the faces of the cube.
– It has 6 square faces.
– The 6 faces are congruent.
– Since the faces are square in shape, the sides of a cube have equal dimensions i.e., L = B = H.
Question 9.
Identify the length, width, and height of the figure you formed.
Answer:
a sample answer is given:
length = 5 units; width = 5 units; height = 5 units
– Since the faces are square in shape, the sides of a cube have equal dimensions i.e., L = B = H.
– Volume is the quantity of space enclosed within a three-dimensional closed surface. Volume is often measured numerically using the SI unit, the cubic metre. So, the volume of a cube = S^3.
Apply It
Question 10.
The rectangular prism-shaped building shown on the right was used for the 2008 Olympics in Beijing, China. What two-dimensional figures form the sides of the building?

Including the floor, how many faces are there?
Answer:
– The squares and rectangles form the sides of the building.
– It has 6 faces.
Question 11.
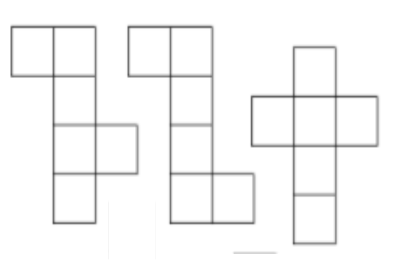
Mathematical PRACTICE Model Math Draw two different nets that would fold to form a cube with length, width, and height each 4 units.
Answer:
Nets of a cube:
– A geometry net is a two-dimensional shape that can be folded to form a 3-dimensional figure.
– A net is a pattern made when the surface of a three-dimensional figure is folded such that it shows each face of the figure.
The net of a cube means the different orientations in which the faces of a cube can be opened and aligned on a flat surface.
Question 12.
Farmers have learned how to grow watermelons in the shape shown at the right. What three-dimensional figure is the watermelon?

Answer:
Cube
Explanation:
– It looks like a square face.
– A cube is a solid three-dimensional object which has six square faces, eight vertices and twelve edges. Since the cube has six faces we can call it a regular hexahedron.
– It has 6 square faces.
– It has 8 corner points which are known as vertices.
Write About It
Question 13.
How are nets used to build three-dimensional figures?
Answer:
– A net for a three-dimensional shape is nothing but a skeleton outline in two-dimension which, when folded, results in three-dimensional shapes. To understand this, let us perform the following activity: Take a cardboard box. Cut the edges to lay the box flat. You have now a net for that box. A net is a skeleton outline in 2D as shown in the first figure, which, when folded, results in a 3D shape as shown in the second figure.
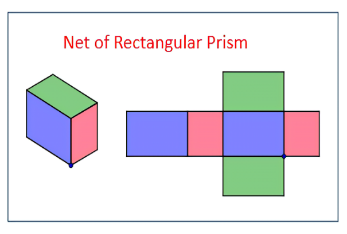
McGraw Hill My Math Grade 5 Chapter 12 Lesson 6 My Homework Answer Key
Vocabulary Check
Fill in each blank with the correct word(s) to complete each sentence.
Question 1.
A three-dimensional figure has _____________, width, and _____________.
Answer: length and height
Definition:
Shapes that can be measured in 3 directions are called three-dimensional shapes. These shapes are also called solids. Length, width, and height (or depth or thickness) are the three measurements of three-dimensional shapes.
Question 2.
A net is a two-dimensional _____________ of a three-dimensional figure.
Answer: representation
Explanation:
A net is a two-dimensional representation of a three-dimensional figure that is unfolded along its edges so that each face of the figure is shown in two dimensions. A net is a pattern made when the surface of a three-dimensional figure is laid out felt showing each face of the figure. A solid may have different nets.
Question 3.
A cube is a three-dimensional figure with six square faces that are _______________.
Answer: congruent
Explanation:
A cube is a three-dimensional object that has 6 congruent square faces. Dimensions of all 6 square faces of the cube are the same.
Practice
For Exercises 4-6. refer to the grid at the right.
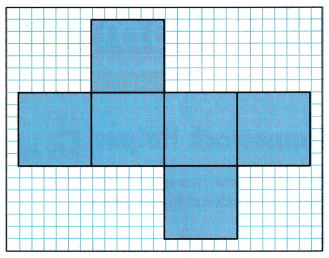
Question 4.
What three-dimensional figure is formed using the net shown?
Answer: cube
Explanation:
Nets of a cube:
– A geometry net is a two-dimensional shape that can be folded to form a 3-dimensional figure.
– A net is a pattern made when the surface of a three-dimensional figure is folded such that it shows each face of the figure.
The six cubes form the faces that join the bottom to the top. As these begin to fold up in the fourth dimension, we see their shadows become distorted in three dimensions (as one face of the cubes moves closer to the light source, its shadow gets larger). Eventually, the faces of the cubes come together and are joined, just as the edges of the squares that form a cube are glued when they are folded together.
Question 5.
What two-dimensional figure forms the sides of the figure? Describe the congruent faces.
Answer:
The square (two-dimensional figure) forms the faces of the cube.
– It has 6 square faces.
– The 6 faces are congruent.
– Since the faces are square in shape, the sides of a cube have equal dimensions i.e., L = B = H.
Question 6.
Identify the length, width, and height of the figure formed.
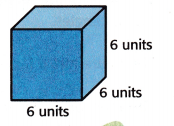
Answer:
Shapes that can be measured in 3 directions are called three-dimensional shapes. These shapes are also called solids. Length, width, and height (or depth or thickness) are the three measurements of three-dimensional shapes.
length = 6 units
width = 6 units
height = 6 units
– Since the faces are square in shape, the sides of a cube have equal dimensions i.e., L = B = H.
Problem Solving
Question 7.
Rachel used a rectangular prism-shaped box to ship a package to her friend. What two-dimensional figure forms the faces of the box?

Including the bottom, how many faces are there? Describe the faces.
Answer:
– A rectangular prism is a three-dimensional shape, that has six faces (two at the top and bottom and four lateral faces). All the faces of the prism are rectangular in shape. Hence, there are three pairs of identical faces here.
– A rectangular prism has 6 faces, 12 edges and 8 vertices
– The top and base of the rectangular prism are always a rectangle
– Like cuboid, it also has three dimensions, i.e., length width and height
– Pairs of opposite faces are identical or congruent.
Question 8.
Joseph is forming a three-dimensional figure using a net. The figure has six congruent square faces. What type of figure did he make?
Answer: cube.
Explanation:
– A cube is a three-dimensional object that has 6 congruent square faces. Dimensions of all 6 square faces of the cube are the same.
– The length, breadth, and height are of the same measurement in a cube since the 3D figure is a square that has all sides of the same length.
Using a net: The net of a cube is formed when the 3D figure with the square faces is flattened by separating at the edges making it into a 2D figure. Through the net of the cube, we can clearly see the six faces i.e. the six square faces that combine together at the edges to form a cube. Here is an image for your reference: