All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 12 Lesson 2 Sides and Angles of Triangles will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 12 Lesson 2 Sides and Angles of Triangles
A triangle is a polygon with three sides and three angles.
Measure It
Measure the sides of each pair of triangles below to the nearest tenth of a centimetre. Then record the measures.
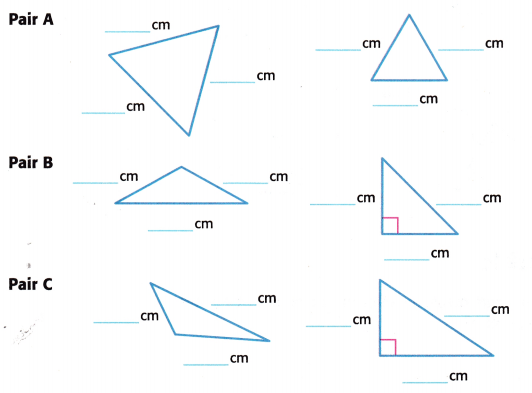
Answer:
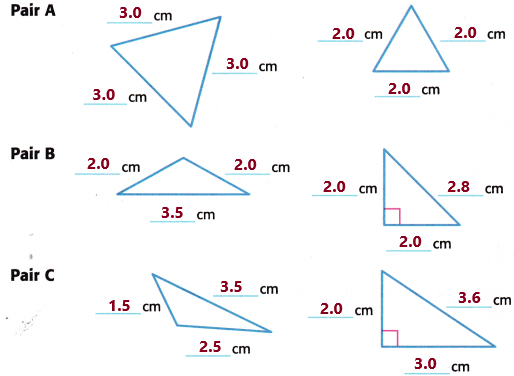
Talk About It
Question 1.
Compare the side lengths of each pair of triangles above. What do you notice?
Answer:
Now we have to compare the above diagram and its measurements:
Pair A:
In pair A, the two triangles have equal sides. So it is said to be all sides are congruent.
In pair B, two sides are congruent.
In pair C, no sides are congruent.
Try It
Measure the angles of each pair of triangles below to the nearest degree. Then record the measures.
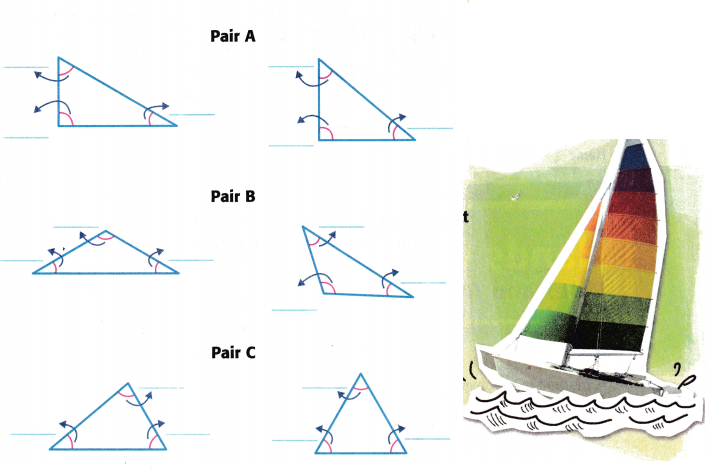
Answer:
Take the protector and measure the angles.
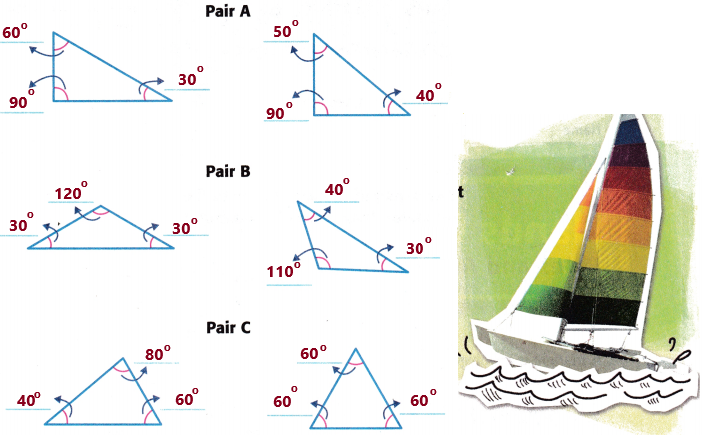
Talk About It
Question 2.
Compare the angle measures of each pair of triangles above. What do you notice?
Answer:
From the above diagram and the angles measured we noticed that:
In pair A: Each has one right angle
In pair B: Each has one obtuse angle.
Obtuse triangle: An obtuse-angled triangle or obtuse triangle is a type of triangle whose one of the vertex angles is bigger than 90°. An obtuse-angled triangle has one of its vertex angles as obtuse and other angles as acute angles i.e. if one of the angles measures more than 90°, then the sum of the other two angles is less than 90°. The side opposite to the obtuse angle is considered the longest.
In pair C: All are acute angles.
Acute triangle: An acute triangle is a triangle in which all three interior angles are less than 90º. Although the three interior angles of the acute triangle lie between 0° to 90°, their sum is always 180 degrees.
Question 3.
Mathematical PRACTICE Make Sense of Problems Explain how a triangle is a special kind of polygon.
Answer: Triangle is a special kind of polygon as it is a polygon that can be formed using the least number of sides which are required to form a polygon. The minimum number of straight lines required to form a polygon is 3 and a polygon formed with it is called a triangle.
Here we need to show why a triangle is a special kind of a polygon. A polygon is any two-dimensional shape that is made by using straight lines and the shape so formed must be a close shape. Hence we must know the minimum of three sides that can be used. So the polygon that can be formed using such three sides can be a triangle. 
Practice It
Measure the sides of each triangle to the nearest tenth of a centimetre. Then describe the number of congruent sides.
Question 4.
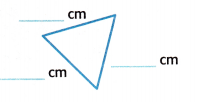
Answer:
Take the scale and measure the sides of the given triangle
Here we need to write the number of congruent sides also.
Now observe the triangle and its measurements:
All sides are having the same measurement which is 2 centimetres.
Therefore, the triangle has 3 congruent sides.
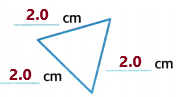
Question 5.
Answer:
Take the scale and measure the sides of the given triangle.
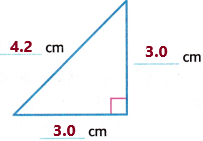
Here we need to write the number of congruent sides also.
Now observe the triangle and its measurements:
Two sides are having the same measurement which is 3 centimetres.
Therefore, the triangle has 2 congruent sides.
Question 6.
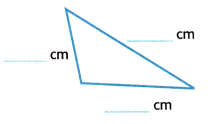
Answer:
Take the scale and measure the sides of the given triangle.
Here we need to write the number of congruent sides also.
Now observe the triangle and its measurements:
No sides are having the same measurement.
Therefore, the triangle has no congruent sides.
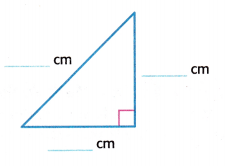
Question 7.
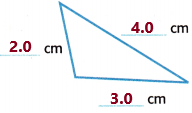
Answer:
Take the scale and measure the sides of the given triangle.
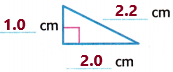
Here we need to write the number of congruent sides also.
Now observe the triangle and its measurements:
No sides are having the same measurement.
Therefore, the triangle has no congruent sides.
Measure the angles of each triangle to the nearest degree. Then describe the number of acute, right, or obtuse angles.
Question 8.
Answer:
Here take a protractor and measure the angles.
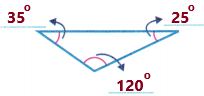
we need to write the number of obtuse, right and acute angles. Observe the diagram and its measurements.
From the above diagram, we can say that the triangle has one obtuse angle and 2 acute angles.
Obtuse angle: “an obtuse angle is an angle which is greater than 90° and less than 180°”. In other words, an obtuse angle is between a right angle and a straight angle.
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
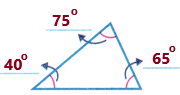
Question 9.
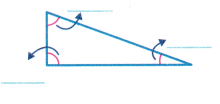
Answer:
Here take a protractor and measure the angles.
we need to write the number of obtuse, right and acute angles. Observe the diagram and its measurements.
From the above diagram, we can say that the triangle has one right angle and 2 acute angles.
Right angle: If the measure of the angle between two rays is exactly equal to 90 degrees or π/2, then the angle is called a right angle.
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
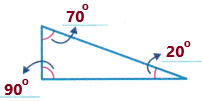
Question 10.
Answer:
Here take a protractor and measure the angles.
we need to write the number of obtuse, right and acute angles. Observe the diagram and its measurements.
From the above diagram, we can say that the triangle has 3 acute angles.
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
Question 11.
Answer:
Here take a protractor and measure the angles.
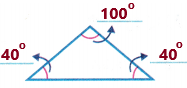
we need to write the number of obtuse, right and acute angles. Observe the diagram and its measurements.
From the above diagram, we can say that the triangle has one obtuse angle and 2 acute angles.
Obtuse angle: “an obtuse angle is an angle which is greater than 90° and less than 180°”. In other words, an obtuse angle is between a right angle and a straight angle.
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
Apply It
Question 12.
In music, the “triangle is an instrument with three congruent sides. If you know that the perimeter of the triangle is 18 inches, what is the measure of one side?

Answer:
The above-given:
The perimeter of a triangle = 18
we need to find out the measure of one side. Let it be S.
The sum of the lengths of the sides is the perimeter of any polygon. In the case of a triangle,
Perimeter = Sum of the three sides
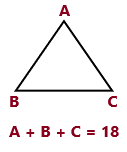
The triangle has 3 sides. so divide the perimeter and number of sides of the triangle to get the answer.
S = 18 / 3
S = 6
Therefore, the measure of one side is 6 inches.
Question 13.
Mathematical PRACTICE Use Math Tools Measure the angles in the triangle shown. What type(s) of angles are in the triangle shown?
Answer: Acute angle
Explanation:
Take a protractor and measure the angle. It is less than 90 degrees.
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
Question 14.
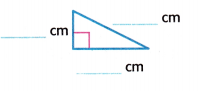
Refer to Exercise 13. Measure the sides of the triangle. Then describe the number of congruent sides.
Answer:
Take a scale and measure the triangle given
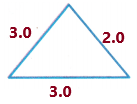
Here we need to write the number of congruent sides also.
Now observe the triangle and its measurements:
Two sides are having the same measurement which is 3 centimetres.
Therefore, the triangle has 2 congruent sides.
Question 15.
Mathematical PRACTICE Which One Doesn’t Belong? Circle the triangle that does not belong with the other three. Explain your reasoning.

Answer:
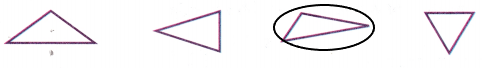
It is the only triangle that does not have at least two congruent sides.
Write About It
Question 16.
How are all triangles the same and how can they be different?
Answer:
Two triangles will be similar if the angles are equal (corresponding angles) and the sides are in the same ratio or proportion (corresponding sides). Similar triangles may have different individual lengths of the sides of triangles but their angles must be equal and their corresponding ratio of the length of the sides must be the same. They can differ in the number of congruent sides and angles measures.
McGraw Hill My Math Grade 5 Chapter 12 Lesson 2 My Homework Answer Key
Practice
Measure the sides of each triangle to the nearest tenth of a centimetre. Then describe the number of congruent sides.
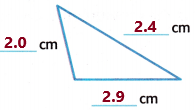
Question 1.
Answer:
Take a scale and measure the triangle given.
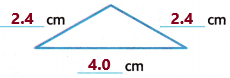
Here we need to write the number of congruent sides also.
Now observe the triangle and its measurements:
Two sides are having the same measurement which is 2.4 centimetres.
Therefore, the triangle has 2 congruent sides.
Question 2.
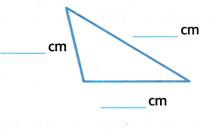
Answer:
Take a scale and measure the triangle given.
Here we need to write the number of congruent sides also.
Now observe the triangle and its measurements:
No sides are having the same measurement.
Therefore, the triangle has no congruent sides.
Measure the angles of each triangle to the nearest degree. Then describe the number of acute, right, or obtuse angles.
Question 3.
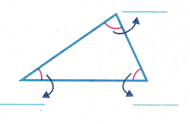
Answer:
Take the protractor and measure the angles.
we need to write the number of obtuse, right and acute angles. Observe the diagram and its measurements.
From the above diagram, we can say that the triangle has 3 acute angles.
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
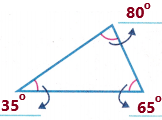
Question 4.
Answer:
Take the protractor and measure the angles.
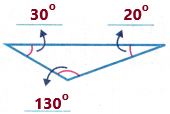
we need to write the number of obtuse, right and acute angles. Observe the diagram and its measurements.
From the above diagram, we can say that the triangle has one obtuse angle and 2 acute angles.
Obtuse angle: “an obtuse angle is an angle which is greater than 90° and less than 180°”. In other words, an obtuse angle is between a right angle and a straight angle.
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
Problem Solving
Question 5.
Measure the sides of the triangle shown. How many sides of the triangle are congruent?
Answer:
Take the scale and measure the sides of the above-given triangle
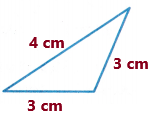
Here we need to write the number of congruent sides also.
Now observe the triangle and its measurements:
Two sides are having the same measurement which is 3 centimetres.
Therefore, the triangle has 2 congruent sides.
Question 6.
Refer to the triangle in Exercise 5. Measure the angles of the triangle shown. How many angles of the triangle are congruent?
Answer:
Take the protractor and measure the angles.
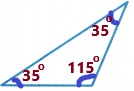
we need to write the number of obtuse, right and acute angles. Observe the diagram and its measurements.
From the above diagram, we can say that the triangle has one obtuse angle and 2 acute angles.
Therefore, 2 angles are congruent.
Obtuse angle: “an obtuse angle is an angle which is greater than 90° and less than 180°”. In other words, an obtuse angle is between a right angle and a straight angle.
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
Question 7.
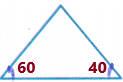
In billiards, a rack is used to organize billiard balls at the beginning of the game. Jason is making the wood rack and found that each angle is congruent and that the sum of the angles is 180°. What is the measure of each angle?

Answer:
The above-given:
The sum of angles = 180 degrees.
We need to measure each angle. Let it be A.
The triangle has 3 sides and 3 angles.
A = 180 / 3
A = 60
Therefore, each angle measures 60 degrees.
Question 8.
Measure each angle of the triangle. How many acute angles does the triangle have?
Answer:
The triangle has 3 sides and 3 angles.
We need to write the number of acute angles the triangle has.
The diagram and angles measured are shown below:
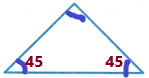
Acute angles: An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees).
The angle measured is 45 degrees.
Therefore, there are two acute angles.