All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 12 Lesson 10 Build Composite Figures will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 12 Lesson 10 Build Composite Figures
A composite figure is made up of two or more three-dimensional figures.
Build It
A composite figure is shown below. Use centimetre cubes to build the figure.


Answer:
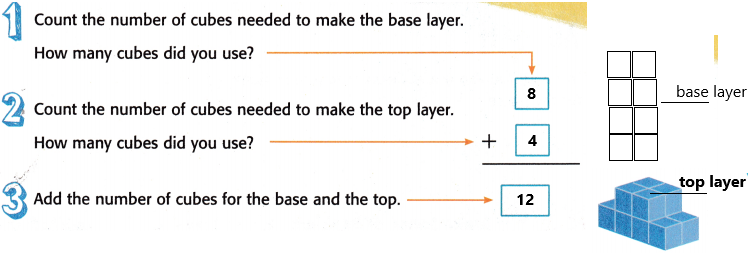
Talk About It
Question 1.
How many cubes did it take to build the figure?
Answer:
The number of cubes taken to build the figure is 12.

Question 2.
What is the volume of the composite figure?
_____________ cubic centimeters
Answer:
The volume of the composite figure is 12 cubic centimetres.
Try It
Separate the composite figure into two rectangular prisms. Then find the volume of each prism.
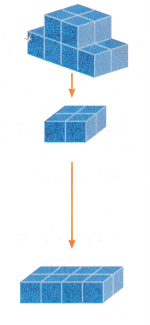
1. Find the volume of the top prism.
V = l × w × h
V = __________ × ___________ × ____________
V = ___________
The volume of the top prism is _____________ cubic centimeters.
Answer:
To find the volume of the top prism, we need to know the length, width, and height.

from the top prism, length = 2; width = 2; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 2 x 2 x 1
V = 4
Therefore, the volume of the top prism is 4 cubic centimetres.
2. Find the volume of the bottom prism.
V = l × w × h
V = __________ × ___________ × ____________
V = ___________
The volume of the bottom prism is _____________ cubic centimeters.
Answer:
To find the volume of the bottom prism, we need to know the length, width, and height.
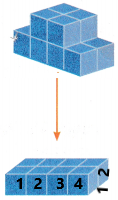
from the bottom prism, length = 4; width = 2; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 2 x 1
V = 8
Therefore, the volume of the bottom prism is 8 cubic centimetres.
3. Add the volumes to find the volume of the composite figure.
________ + ___________ = ____________
So, the volume of the composite figure is ______________ cubic centimeters.
Answer:
Now add the volumes of top and bottom prisms.
V(add) = 4 + 8
V(add) = 12
Therefore, the volume of the composite figure is 12 cubic centimetres.
Talk About It
Question 3.
Explain how you can use addition to find the volume of a composite figure.
Answer:
To calculate the volume of a composite solid, simply split it into smaller solids and calculate their separate volumes. The volumes of each of the individual solids are then added to give the total volume of the composite solid.
Question 4.
Mathematical PRACTICE Make Sense of Problems Explain how you would find the volume of the composite figure shown.

Answer:
Now we split the composite figure into two types.
Divide the figure into 4 prisms and find the volume of each prism. Then add the volumes of each prism.
Question 5.
What is the volume of the figure in Exercise 4?
_______________ cubic centimeters
Answer:
The above figure is divided into 4 prisms:
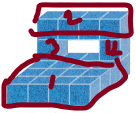
1. from the base prism, length = 4; width = 4; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 4 x 1
V = 16
Therefore, the volume of the base prism is 16 cubic centimetres.
2. from the top prism, length = 4; width = 1; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 1 x 1
V = 4
Therefore, the volume of the top prism is 4 cubic centimetres.
The remaining two prisms are height = 1; width = 1; length = 1
Volume = length x width x height
3. V = 1 x 1 x 1 = 1 and 4. V = 1 x 1 x 1 = 1
Now add all the volumes of all 4 prisms:
V(add) = 16 + 4 + 1 + 1
V(add) = 22
Therefore, the volume of the composite figure is 22 cubic centimetres.
Practice It
Use the model at the right to build the composite figure using centimetre cubes.

Question 6.
Separate the figure into prisms. Make a drawing of each prism used to build the composite figure.
Answer:
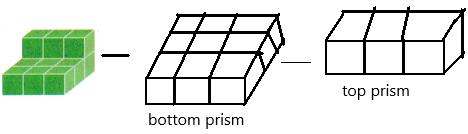
The prism is divided into bottom and top
Now we need to find out the volume of the two prisms and then add both values.
Question 7.
How many cubes did it take to build the figure?
_____________ cubic centimeters
Answer:
1. from the base prism, length = 3; width = 3; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 3 x 3 x 1
V = 9
Therefore, the volume of the base prism is 9 cubic centimetres.
2. from the top prism, length = 4; width = 1; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 3 x 1 x 1
V = 3
The volume of the cube is 3 cubic centimetres.
Now add all the volumes of all 2 prisms:
V(add) = 9 + 3
V(add) = 12
Therefore, the number of the composite figure to build is 12 cubic centimetres.
Question 8.
What is the volume of this figure?
_____________ cubic centimeters
Answer: 12 cubic centimetres
Explanation:
Now add all the volumes of all 2 prisms:
V(add) = 9 + 3
V(add) = 12
Therefore, the volume of the composite figure is 12 cubic centimetres.
Use the model at the right to build the composite figure using centimetre cubes.

Question 9.
Separate the figure into prisms. Make a drawing of each prism used to build the composite figure.
Answer:

Question 10.
How many cubes did it take to build the figure?
Answer:
1. from the base prism, length = 4; width = 3; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 3 x 1
V = 12
Therefore, the volume of the base prism is 12 cubic centimetres.
2. from the top prism, length = 4; width = 2; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 2 x 1
V = 8
The volume of the cube is 8 cubic centimetres.
3. from the top prism, length = 4; width = 1; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 1 x 1
V = 4
The volume of the cube is 8 cubic centimetres.
Now add all the volumes of all 3 prisms:
V(add) = 12 + 8 + 4
V(add) = 24.
Therefore, the number of the composite figure to build is 24 cubic centimetres.
Question 11.
What is the volume of this figure?
_____________ cubic centimeters
Answer:
Now add all the volumes of all 3 prisms:
V(add) = 12 + 8 + 4
V(add) = 24.
Therefore, the volume of the composite figure to build is 24 cubic centimetres.
Apply It
Tanela arranged centimeter cubes into the composite figure shown. Use the composite figure for Exercises 12 and 13.

Question 12.
Mathematical PRACTICE Model Math Separate the figure into prisms. Make a drawing of each prism used to build the composite figure.
Answer:
The above-given figure can be split into two prisms.
The figure can be shown as:
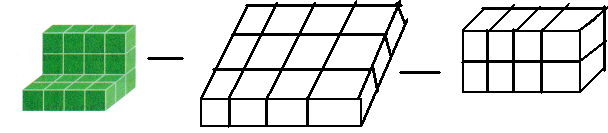
Question 13.
What is the volume of the composite figure? Check your answer by building a model and counting the number of cubes.
______________ cubic centimeters
Answer:
1. from the base prism, length = 4; width = 3; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 3 x 1
V = 12
Therefore, the volume of the base prism is 12 cubic centimetres.
2. from the top prism, length = 4; width = 2; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 2 x 1
V = 8
The volume of the cube is 8 cubic centimetres.
Now add all the volumes of all 2 prisms:
V(add) = 12 + 8
V(add) = 20
Therefore, the volume of the composite figure to build is 20 cubic centimetres.
Question 14.
Circle the composite figure that has a volume of 24 cubic centimetres.

Answer:
The volume of the first figure:
1. from the base prism, length = 4; width = 4; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 4 x 1
V = 16
Therefore, the volume of the base prism is 16 cubic centimetres.
2. from the top prism, length = 4; width = 1; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 1 x 1
V = 4
The volume of the cube is 4 cubic centimetres.
The other two prism volumes are 1 and 1
Now add all the prisms: 16 + 4 + 1 + 1 = 22
So, the first one is not correct.
Now let’s check for the second prism:
1. from the base prism, length = 4; width = 4; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 4 x 1
V = 16
Therefore, the volume of the base prism is 16 cubic centimetres.
2. from the top prism, length = 4; width = 2; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 2 x 1
V = 8
The volume of the cube is 8 cubic centimetres.
Now add the prism values we got: 16 + 8 = 24
Therefore, the answer is the second prism.
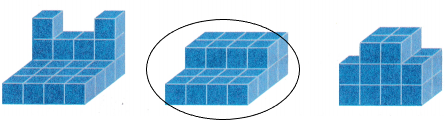
Question 15.
Mathematical PRACTICE Make Sense of Problems Explain how to use the formula of a rectangular prism to find the volume of a composite figure that is composed of rectangular prisms.
Answer:
The formula for the volume of a rectangular prism = base area × height of the prism. Since the base of a rectangular prism is a rectangle, its area will be l × w. This area is then multiplied by the height of the prism to get the volume of the prism.
I can find the volume of each rectangular prism and then add them together to find the total volume.
Write About It
Question 16.
How can you use models to find the volume of composite figures?
Answer:
break up a composite figure into multiple shapes. apply the volume formulas of prisms, to calculate the volume of a composite figure Composite figures is just a combination of simpler figures in disguise. To find the volume of a composite figure, the composite figure must first be divided into simpler figures
The number of cubes in the model represents the volume, In cubic units of the figure.
McGraw Hill My Math Grade 5 Chapter 12 Lesson 10 My Homework Answer Key
Practice
Refer to the composite figure at the right.

Question 1.
How many cubes are needed to build the bottom layer?
Answer:
1. from the base prism, length = 5; width = 4; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 5 x 4 x 1
V = 20
Therefore, the volume of the base prism is 20 cubic centimetres.
Question 2.
How many cubes are needed to build the top two layers?
Answer:
from the top prism, length = 5; width = 1; height = 2
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 5 x 1 x 2
V = 10
The volume of the cube is 10 cubic centimetres.
Question 3.
Use addition to add the bottom and top layers.
Answer:
Now add the bottom and top prism values.
V(add) = bottom prism value + top prism value.
V(add) = 20 + 10
V(add) = 30
The volume of the cube is 30 cubic centimetres.
Question 4.
What is the volume of the composite figure?
____________ cubic centimeters
Answer:
From the above calculations of questions (1), (2), (3).
The volume of the composite figure is 30 cubic centimetres.
Problem Solving
Jared built the composite figure at the right using centimetre cubes.

Question 5.
Separate the figure into prisms. Make a drawing of each prism used to build the composite figure.
Answer:
The figure is split into two prisms. The diagram is shown below:
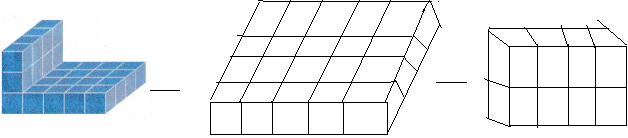
Question 6.
How many cubes did it take Jared to build the figure?
Answer:
1. from the base prism, length = 5; width = 4; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 5 x 4 x 1
V = 20
Therefore, the volume of the base prism is 20 cubic centimetres.
2. from the top prism, length = 4; width = 2; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 4 x 2 x 1
V = 8
The volume of the cube is 8 cubic centimetres.
Question 7.
What is the volume of this figure?
_______________ cubic centimeters
Answer:
From the above calculation question(6)
We need to add the bottom and top prism to get to know the volume of the figure.
V(add) = 20 + 8
V(add) = 28
Therefore, the volume of the figure is 28 cubic centimetres.
Question 8.
Mathematical PRACTICE Find the Error Gabriele built a composite figure using 12 cubes for the bottom layer and 10 cubes for the top layer. She said that the volume of the composite figure was 12 × 10, or 120 cubic centimetres. Find and correct her error.
Answer:
The above-given:
The bottom layer of the prism = 12
The top layer of the prism = 10
She was multiplied so she gets 120 cubic centimetres.
Actually, she should add the two layers but she multiplied. It is the error she did.
The correct answer is she should add that two layers.
12 + 10 = 22
The correct volume is 12 + 10 = 22 cubic centimetres.
Vocabulary Check
Fill in the blank with the correct term or number to complete the sentence.
Question 9.
A composite figure is made up of two or more _______________ figures.
Answer: three-dimensional
The composite figure can be defined as a shape that constitutes more than two-dimensional shapes. When deconstructed, a composite shape is made up of a number of other shapes. A more technical definition of the term is based on the constituent shapes that make up the composite figure. The composite figure is a two-dimensional figure constructed up of basic two-dimensional shapes such as triangles, rectangles, circles, semi-circles, and so on.
Question 10.
The composite figure was built using centimetre cubes. What is the volume of the composite figure shown?

V = ______________ cubic centimeters
Answer:
1. from the base prism, length = 5; width = 2; height = 1
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 5 x 2 x 1
V = 10
Therefore, the volume of the base prism is 10 cubic centimetres.
2. from the top prism, length = 3; width = 2; height = 2
Now we know the values. So substitute the values in the formula.
Volume (V) = length (l) x width (w) x height (h)
V = 3 x 2 x 2
V = 12
The volume of the cube is 12 cubic centimetres.
Now add both layers:
V(add) = bottom layer + top layer
V(add) = 10 + 12
V(add) = 22
Therefore, the volume of the given prism is 22 cubic centimetres.