All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 12 Geometry will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 12 Geometry
Essential Question
How does geometry help me solve problems in everyday life?
Answer:
– When you learn to use geometry you also learn to think logical. This is very important in everyday life, as not everything is easy and understandable. When thinking logically many difficult problems can be erased and simple solutions can be found.
– When we know how to apply and understand the relationship between shapes and sizes we will be better prepared to use them in our everyday lives. Geometry will assist us in doing that because it provides the knowledge of how to deal with measurements and relationships of lines, angles, surfaces and solids.
Am I Ready
Name the number of sides and the number of angles in each figure.
Question 1.

____________ sides and ____________ angles
Answer:
The name of the shape is a parallelogram.
a parallelogram has 4 sides and 4 angles.
– A parallelogram is a two-dimensional shape. It has four sides, in which two pairs of sides are parallel.
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. The Sum of all the interior angles equals 360 degrees.
Angles of parallelogram:
A parallelogram is a flat 2d shape which has four angles. The opposite interior angles are equal. The angles on the same side of the transversal are supplementary, which means they add up to 180 degrees. Hence, the sum of the interior angles of a parallelogram is 360 degrees.
Question 2.
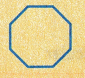
____________ sides and ____________ angles
Answer:
The name of the shape is an octagon
There are 8 sides and 8 angles.
Octagon sides: The octagon is an 8-sided polygon. That means an octagon contains 8 sides. Also, based on the length of these sides, octagons are classified as regular and irregular octagons.
Octagon angles: The octagonal shape contains 8 angles at 8 vertices. Thus, the octagon holds 8 sides and 8 angles. There are 8 interior angles and 8 exterior angles in an octagon. Octagon interior angles sum is equal to 1080 degrees. Also, the sum of all eight exterior angles is equal to 360 degrees. Based on the type of angles, octagons are classified as convex and concave octagons.
Question 3.
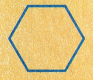
____________ sides and ____________ angles
Answer:
The name of the shape is a hexagon
It has 6 sides and 6 angles.
In geometry, a hexagon is a closed two-dimensional six-sided polygon. It is made up of six line segments and six vertices that form six internal angles. The sum of all the internal angles of a hexagon is 720°.
Question 4.

____________ sides and ____________ angles
Answer:
The shape of the given figure is a triangle
It has 3 sides and 3 angles.
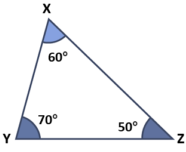
– Triangle is a closed two-dimensional shape. It is a three-sided polygon. All sides are made of straight lines. The point where two straight lines join is the vertex. Hence, the triangle has three vertices. Each vertex forms an angle.
– There are three angles in a triangle. These angles are formed by two sides of the triangle, which meet at a common point, known as the vertex. The sum of all three interior angles is equal to 180 degrees.
Use the figure below for Exercises 5 and 6.

Question 5.
Which side appears to have the same length as side AD?
Answer:

The same length in a rectangle is one side is AD and the other same side is BC.
Question 6.
At which point do sides AB and BC meet?
Answer:
The side AB and BC meet at point B.
The figure is shown below:

Question 7.
Kai is drawing a triangle with all three sides that are equal. Draw a sketch of this triangle.
Answer:
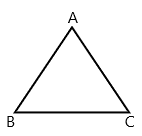
Def: a triangle is a type of polygon, which has three sides, and the two sides are joined end to end is called the vertex of the triangle. An angle is formed between two sides. This is one of the important parts of geometry.
Shape: Triangle is a closed two-dimensional shape. It is a three-sided polygon. All sides are made of straight lines. The point where two straight lines join is the vertex. Hence, the triangle has three vertices. Each vertex forms an angle.
How Did I Do?
Shade the boxes to show the problems you answered correctly.
![]()
Answer:
![]()
My Math Words
Review Vocabulary
acute angle
angles lines
obtuse angle
parallel
perpendicular
right angle
Making Connections
Use the review word; to classify geometric shapes.
Draw an example of two of the words used above.
Answer:
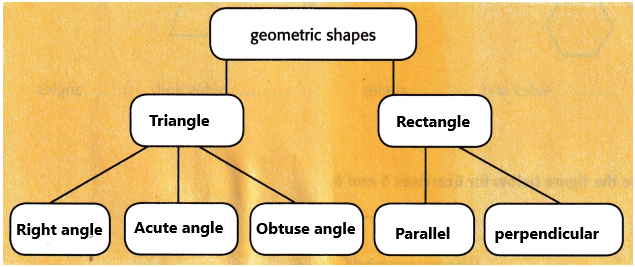
Triangle:
Rectangle: 
My Vocabulary Cards
Ideas for Use
- Design a crossword puzzle. Use the definition for each word as the clues.
- Group 2 or 3 common words. Add a word that is unrelated to the group. Then work with a friend to name the unrelated word.
A characteristic of a figure.
Use attributes to describe the sides or angles of a rectangle.
Answer:
– It has four sides and four vertices
– Each vertex has an angle equal to 90 degrees
– The opposite sides are equal and parallel
– Diagonals bisect each other
– Perimeter is equal to twice the sum of its length and breadth
– The area is equal to the product of its length and breadth
– It’s a parallelogram with four right angles.
– Sum of all interior angles equal to 360 degrees
A triangle with 3 acute angles.
Explain how to determine if a triangle is an acute triangle.
Answer:
Triangles can be classified on the basis of angles and sides. An acute triangle is one that is classified on the basis of the measurement of angles. If all the interior angles of a triangle are less than 90°, then the triangle is said to be an acute triangle.
There are a few important properties that help us identify an acute triangle:
– According to the angle sum property, all the three interior angles of an acute triangle add up to 180°.
– A triangle cannot be a right-angled triangle and an acute-angled triangle at the same time.
– A triangle cannot be an acute-angled triangle and an obtuse-angled triangle at the same time.
– The angle property of the acute triangle says the interior angles of an acute triangle are always less than 90° or lie between (0° to 90°). The side opposite to the smallest angle is the smallest side of the triangle.
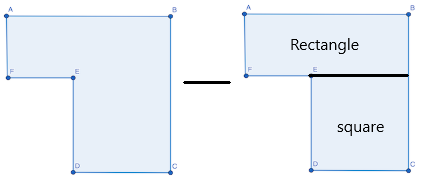
A figure is made of two or more three-dimensional figures.
Composite comes from composing, “to put together.” How does this help you understand a composite figure?
Answer:
A composite figure is a combination of two or more shapes. The name composite comes from the Latin word ”componere” which translates as ”put together.” A composite shape is also known as a combined figure and can be made up of the same or different shapes. For example, a composite figure may be made by combining two rectangles together. A composite figure may also be formed by a square and a triangle.
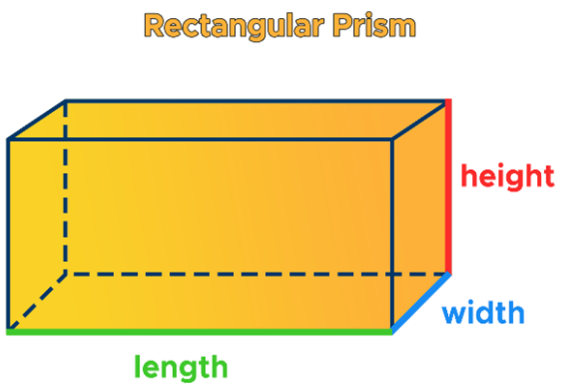
Two parallel congruent faces in a prism.
Describe the base of a rectangular prism.
Answer:
– In geometry, a rectangular prism is a polyhedron with two congruent and parallel bases. It is also called a cuboid. A rectangular prism has six faces, and all the faces are in a rectangle shape and have twelve edges.
– A prism with rectangular bases is called a rectangular prism. A right rectangular prism is a prism that has six faces that are rectangles, and all angles are right angles.
– Vertices of a rectangular prism = 8
– Edges of a rectangular prism = 12
– Faces of a rectangular prism= 6 (including bases)
There are some properties:
– A rectangular prism has 6 faces, 12 edges and 8 vertices
– The top and base of the rectangular prism are always a rectangle
– Like a cuboid, it also has three dimensions, i.e., length width and height
– Pairs of opposite faces are identical or congruent
– For a right rectangular prism, the lateral faces are rectangle
– For oblique rectangular prims, the lateral faces are parallelogram
– It has a rectangular cross-section
– It looks exactly like a cuboid
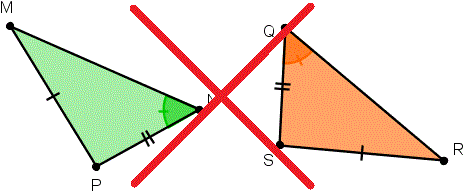
Two figures that have the same size and shape.
Draw 2 congruent figures in the space below.
Answer:
In geometry, congruent means identical in shape and size. Congruence can be applied to line segments, angles, and figures. Any two line segments are said to be congruent if they are equal in length. Two angles are said to be congruent if they are of equal measure. Two triangles are said to be congruent if their corresponding sides and angles are equal.

Angles of a figure that are equal in measure.
Draw an example of a figure with congruent angles. Then draw a non-example. Cross out the non-example.
Answer:
Congruent angles are two or more angles that are identical to each other. Thus, the measure of these angles is equal to each other. The type of angles does not make any difference in the congruence of angles, which means they can be acute, obtuse, exterior, or interior angles.
Below is the list of rules for congruence angles:
– The only condition for two angles to be congruent is that the measures of angle measures are the same.
– The length and direction of the two arms making up these congruent angles are irrelevant.
congruent angles:
A three-dimensional figure with six faces that are congruent squares.
What does a cube mean when it is used as a verb?
Answer:
The verb CUBE has 2 senses: 1. raise to the third power. 2. cut into cubes. CUBE used as a verb is rare.
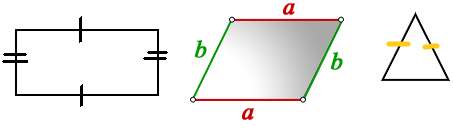
Sides of a figure that are equal in length.
Draw two figures that each has at least two congruent sides.
Answer:
In geometry, congruent means identical in shape and size. Congruence can be applied to line segments, angles, and figures. Any two line segments are said to be congruent if they are equal in length. Two angles are said to be congruent if they are of equal measure. Two triangles are said to be congruent if their corresponding sides and angles are equal. Here we need to draw the figures that are having at least two congruent sides.
Ideas for Use
- Write a tally mark on each card every time you read the word in this chapter or use it in your writing. Challenge yourself to use at least 10 tally marks for each word card.
- Draw or write additional examples for each card. Be sure your examples are different from what is on the front of the card.
The line segment is where two faces of a three-dimensional figure meet.
Describe a real-world example of an edge.
Answer:
The line segment which acts as an interface between two faces is called an edge. Sometimes it is also described as the line segment joining two vertices.
The unit of measure for volume.
Name three other units of measurement in math and what they measure.
Answer:
Volume Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI-derived units (such as the cubic meter and litre) or by various imperial units (such as the gallon, quart, and cubic inch).
A flat surface.
Read and solve this riddle: I am a triangular prism. I have nine edges and six vertices. How many faces do I have?
Answer:
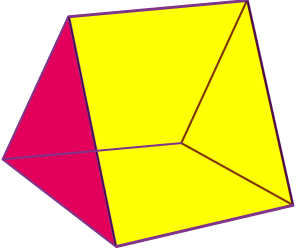
– It has a total of 9 edges, 5 faces, and 6 vertices (which are joined by the rectangular faces).
– It has two triangular bases and three rectangular sides
– If the triangular bases are equilateral and the other faces are squares, instead of a rectangle, then the triangular prism is said to be semiregular
A triangle with three congruent sides.
The prefix Equi- means equal.n Lot is a Latin root meaning “side. Explain how these word parts can help you remember this definition.
Answer:
In geometry, an equilateral triangle is a triangle that has all its sides equal in length. Since the three sides are equal therefore the three angles, opposite to the equal sides, are equal in measure. Therefore, it is also called an equiangular triangle, where each angle measure 60 degrees. the three angles of the equilateral triangle are congruent and equal to 60 degrees. The sum of all three angles of an equilateral triangle is equal to 180 degrees. 60° + 60° + 60° = 180°.
– The shape of an equilateral triangle is regular. The word ‘Equilateral’ is formed by the combination of two words, i.e., “Equi” meaning equal and “Lateral” meaning sides. An equilateral triangle is also called a regular polygon or regular triangle since all its sides are equal.
A triangle with at least two congruent sides.
Draw an example of an isosceles triangle.
Answer:
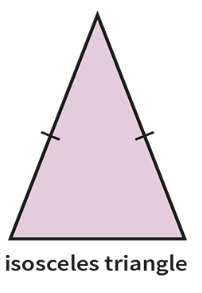
An Isosceles triangle is a triangle that has two equal sides. Also, the two angles opposite the two equal sides are equal. In other words, we can say that “An isosceles triangle is a triangle which has two congruent sides“.
Properties:
– As the two sides are equal in this triangle, the unequal side is called the base of the triangle
– The angles opposite to the two equal sides of the triangle are always equal
– The altitude of an isosceles triangle is measured from the base to the vertex (topmost) of the triangle
– A right isosceles triangle has a third angle of 90 degrees
A polygon with six sides and six angles.
How are hexagons a subcategory of polygons?
Answer:

A hexagon is a polygon with six angles.
– Hexagons are polygons enclosed by six sides. We’ve learned that polygons are two-dimensional figures enclosed by straight lines, so hexagons are 2D figures enclosed by six straight lines. Hexagons also have six vertices, edges, and angles each.
A triangle with 1 obtuse angle and 2 acute angles.
Compare a right triangle to an obtuse triangle. Use the space below to draw your comparison.
Answer:
– A right triangle is a triangle where one of its angles is a right angle (i.e. 90°). The other two angles are acute angles.
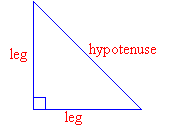
– A right triangle can be isosceles if the two legs are equal in length. A right isosceles triangle will have a 90º angle and two 45º angles.
An obtuse-angled triangle is a triangle in which one of the interior angles measures more than 90° degrees. In an obtuse triangle, if one angle measures more than 90°, then the sum of the remaining two angles is less than 90°.
– Since the sum of all the angles in a triangle is 180º, only one angle in the triangle can be an obtuse angle, the other two angles must be acute angles.
A two-dimensional pattern of a three-dimensional figure.
What does net mean in this sentence? The soccer player’s hand become tangled in the goal’s net
Answer:
Net is a two-dimensional pattern of a three-dimensional figure that can be folded to form the figure.
– In other words, net is a flattened three-dimensional figure which can be turned into the solid by folding it.
Ideas for Use
- Develop categories for the words. Sort them by category. Ask another student to guess each category.
- Draw or write examples for each card. Be sure your examples are different from what is shown on each card.
A quadrilateral in which each pair of opposite sides is parallel and congruent.
How does parallel help you remember the meaning of parallelogram?
Answer:
– A parallelogram is a flat shape with four straight, connected sides so that opposite sides are congruent and parallel. This means a parallelogram is a plane figure, a closed shape, and a quadrilateral.
– A parallelogram is a two-dimensional shape. It has four sides, in which two pairs of sides are parallel. Also, the parallel sides are equal in length. If the length of the parallel sides is not equal in measurement, then the shape is not a parallelogram. Similarly, the opposite interior angles of parallelogram should always be equal. Otherwise, it is not a parallelogram.
A polygon with eight sides.
Okto is a Greek root meaning TMeight” How can this help you remember this vocabulary word?
Answer:
Octo is the greek word for eight
TMeight means ‘eight’ in Greek.
We know that A polygon with eight sides is octagon. In that way we can easily remember the word.
– An octagon is a closed two-dimensional figure with eight sides, eight vertices and eight interior angles. If all the sides and interior angles of an octagon are of equal measure, then it is called a regular octagon otherwise an irregular octagon.
A closed figure is made up of line segments that do not cross each other.
Explain why a circle is not a polygon.
Answer:
The closed figures made up of only line segments that do not cross each other are called polygon.
– A circle is not a polygon. A polygon is a closed figure on a plane created by a finite number of end-to-end linked line segments. Because a circle is curved, it cannot be constructed from line segments and so does not meet the criteria for being a polygon.
A polygon with five sides.
How can the Pentagon, a government building in Washington, D.C., help you remember the pentagon?
Answer:
A polygon with five sides is called a pentagon.
The Pentagon is the headquarters building of the United States Department of Defense. It was constructed on an accelerated schedule during World War II. As a symbol of the U.S. military, the phrase The Pentagon is often used as a metonym for the Department of Defense and its leadership.
A quadrilateral with four right angles; opposite sides are equal and parallel.
Compare a rectangle with a square.
Answer:
A quadrilateral with four right angles is square
opposite sides are equal and parallel is a rectangle.
– The difference between a square and a rectangle is that a square has all equal sides, whereas, in a rectangle, the opposite sides are equal. Squares and rectangles are the most common shapes seen around us. Apparently, they seem to be quite similar, however, mathematically, they are different. In other words, a square is a rectangle in which the adjacent sides are equal and the interior angles are equal to 90°.
– Although squares and rectangles are quadrilaterals, there are certain properties that differentiate them:
square: A square is a flat two-dimensional shape (2D shape) that has four equal sides, four interior right angles, and four vertices. Diagonals of a square are the perpendicular bisector of each other.
Rectangle: A rectangle is a two-dimensional shape in which the opposite sides are equal. It has four equal angles and four vertices. All four angles of a rectangle measure 90°. Diagonals of a rectangle are not perpendicular bisectors of each other.
A three-dimensional figure with two parallel, congruent faces, called bases. At least three faces are rectangles.
Look at the orange prism on the front of the card. What shape are its bases?
Answer:
A prism is a three-dimensional figure with two parallel, congruent bases. The bases, which are also two of the faces, can be any polygon.
– The name of the orange prism is a triangular prism.
– Triangular prism bases are of triangle shape.
A polygon in which all sides and angles are congruent
What is one way to determine if a polygon is regular?
Answer:
A polygon in which all sides and angles are congruent is a regular polygon.
The only way we determine is all the sides and interior angles of a regular polygon are all equal.
– The most common examples of regular polygons are square, rhombus, equilateral triangle etc.
A prism that has rectangular bases.
Describe the faces of any rectangular prism.
Answer:
Note: The faces of rectangular prisms are the plane surfaces. In total, a prism has six faces and they are all rectangular. An important feature of faces is that each face meets four other faces at right angles, that is, 90-degree angles.
A rectangular prism is a prism whose bases (the top face and the bottom face) are also rectangles. It has 6 faces in all, out of which there are 3 pairs of identical opposite faces, i.e., all the opposite faces are identical in a rectangular prism. It has three dimensions, length, width, and height. Some examples of a rectangular prism in real life are rectangular tissue boxes, school notebooks, laptops, fish tanks, large structures such as cargo containers, rooms, storage sheds, etc.
Ideas for Use
- Practice your penmanship! Write each word in cursive.
- Sort cards so that only polygons are displayed. Explain your sorting to a partner.
A triangle with 1 right angle and 2 acute angles.
Is it possible for a right triangle to have more than one right angle? Explain.
Answer:
A triangle with one right angle and two acute angles is called a right-angled triangle.
No, a triangle can never have 2 right angles. A triangle has exactly 3 sides and the sum of interior angles sum up to 180°. So, if a triangle has two right angles, the third angle will have to be 0 degrees which means the third side will overlap with the other side. Thus, it is not possible to have a triangle with 2 right angles.
A parallelogram with four congruent sides.
Explain whether a rectangle is a rhombus.
Answer:
Parallelograms with four congruent sides are Square and Rhombus.
A rhombus is a parallelogram with all its sides equal. This means that for a rectangle to be a rhombus, its sides must be equal. When this is satisfied, we have a square. A rectangle can be a rhombus only if has extra properties which would make it a square.
A rectangle and a rhombus are both types of parallelograms.
However, they have different properties in their sides, angles and diagonals.
A rectangle has all its angles at 90°
A rectangle has two pairs of equal sides – two longer sides and two shorter sides.
The diagonals of a rectangle are equal but do not intersect at 90°
The opposite angles of a rhombus are equal. There are two obtuse angles and two acute angles.
All four sides of a rhombus are equal.
The diagonals are not equal, but they intersect at 90°
Therefore, a rectangle is not a rhombus.
A parallelogram with four congruent sides and four right angles.
Is a square also a rectangle? Explain.
Answer:
A square is one of the most basic geometric shapes. It is a special case of a parallelogram that has four congruent sides and four right angles. Asquare is also a rectangle because it has two sets of parallel sides and four right angles. Yes, a square is a special type of rectangle because it possesses all the properties of a rectangle. Similar to a rectangle, a square has:
– interior angles which measure 90∘ each.
– opposite sides that are parallel and equal.
– two diagonals that bisect each other and are equal.
A triangle with no congruent sides.
Draw a scalene triangle below.
Answer:
A scalene triangle has no congruent sides, all sides are different.
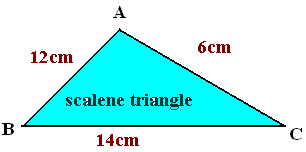
In geometry, Scalene Triangle is a triangle that has all its sides of different lengths. It means all the sides of a scalene triangle are unequal and all the three angles are also of different measures.
Some of the important properties of the scalene triangle are as follows:
– It has no equal sides.
– It has no equal angles.
– It has no line of symmetry.
– It has no point symmetry.
– The angles inside this triangle can be acute, obtuse or right angles.
– If all the angles of the triangle are less than 90 degrees(acute), then the centre of the circumscribing circle will lie inside a triangle.
– In a scalene obtuse triangle, the circumcenter will lie outside the triangle.
– A scalene triangle can be an obtuse-angled, acute-angled or right-angled triangle.
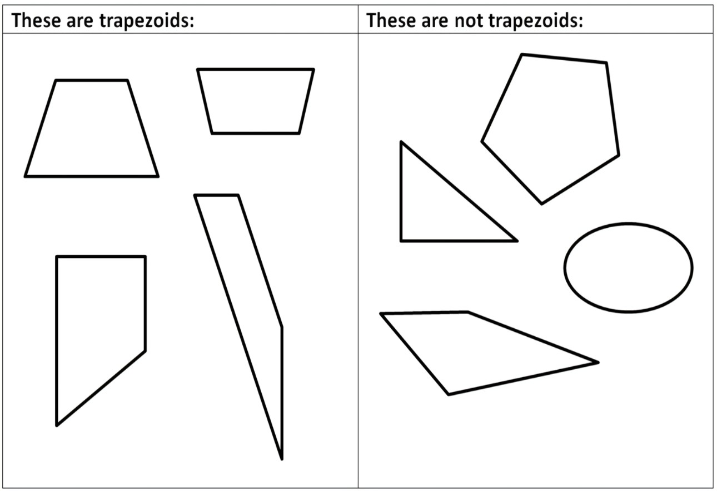
A quadrilateral with exactly one pair of opposite sides parallel.
Draw a picture of two quadrilaterals-one that is a trapezoid and one that is not.
Answer:
A trapezium is a quadrilateral with exactly one pair of parallel sides. One pair of opposite sides is parallel and the other pair is not parallel.
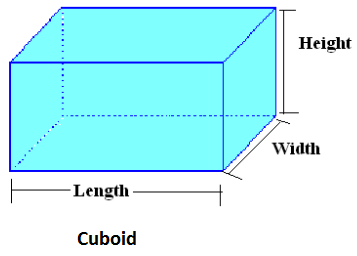
A figure that has length, width, and height
Write a tip to help you remember the number of dimensions for three-dimensional figures.
Answer:
A figure that has length, width, and height is a three-dimensional shape.
Tip: shapes that can be measured in 3 directions are called three-dimensional shapes.
Length, width, and height are the tools that are used to find the dimensions of an object. When we refer to two-dimensional shapes (2D shapes), we use the length and width, whereas when we refer to three-dimensional shapes (3D shapes) we use the height along with the length and width.
The longer side of the shape is length; the shorter side of the shape is width.
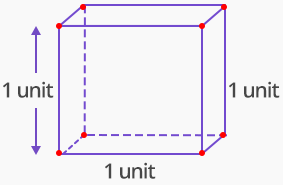
A cube with a side length of one unit
Draw a rectangular prism below that has a volume of 8 unit cubes.
Answer:
A cube with a side length of one unit is a unit cube.
A unit cube, more formally a cube of side 1, is a cube whose sides are 1 unit long. The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units.
Rectangular prism:
Finding the volume of a rectangular prism is to do is to multiply the length, width, and height together:
The volume of a Rectangular Prism (V) = l × b × h
The base length, base width and height of the rectangular prism as 2 units, 2 units and 2 units respectively. Find the volume of the rectangular prism
Solution:
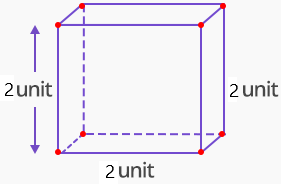
Given,
b = 2 units
l = 2 units
h = 2 units
Using the volume of a rectangular prism formula,
The volume of a Rectangular Prism = lbh
= 2 × 2 × 2
= 8 cubic units.
A prism that has triangular bases.
Describe the bases of any triangular prism.
Answer:
A prism that has triangular bases is called a triangular prism.
A triangular prism is a polyhedron made up of two triangular bases and three rectangular sides. It is a three-dimensional shape that has three side faces and two base faces, connected to each other through the edges.
Right triangular prism: A right triangular prism has its three rectangular sides congruent. Also, the two triangular bases are parallel and congruent to each other. The rectangular or lateral faces are perpendicular to the triangular bases.
Ideas for Use
- Write key concepts from some lessons on the front of blank cards. Write a few examples on the back of each card to help you study.
- Use a blank card to write this chapter’s essential question. Use the back of the card to write or draw examples that help you answer the question.
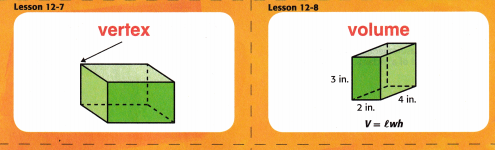
The amount of space inside a three-dimensional figure.
How many measurements do you need to find the volume of a rectangular prism? What are they?
Answer:
The amount of space inside a three-dimensional figure is called volume.
To find the volume of a rectangular prism, multiply its 3 dimensions: length x width x height. The volume is expressed in cubic units.
The point where three or more faces meet on a three-dimensional figure.
How many vertices does a rectangular prism have?
Answer:
The point where three or more faces meet on a three-dimensional figure is called the vertex.
A rectangular prism is a three-dimensional shape, that has six faces (two at the top and bottom and four lateral faces). All the faces of the prism are rectangular in shape. Hence, there are three pairs of identical faces here. Due to its shape, a rectangular prism is also called a cuboid.
The rectangular prism has 8 vertices.
My Foldable
Follow the steps on the back to make your Foldable.

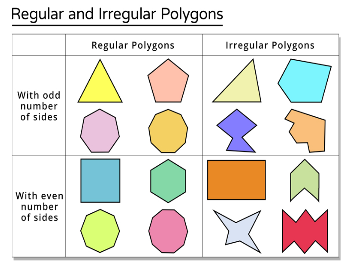
Answer:
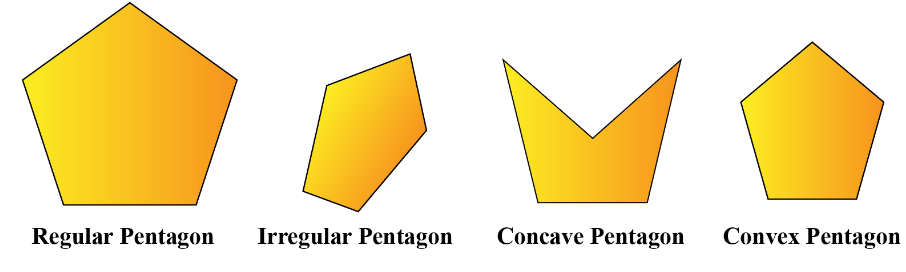
A polygon is said to be regular if all the sides and angles of it are equal. A pentagon with all sides equal and all angles equal is called a regular pentagon. Pentagons that aren’t regular are called irregular pentagons.
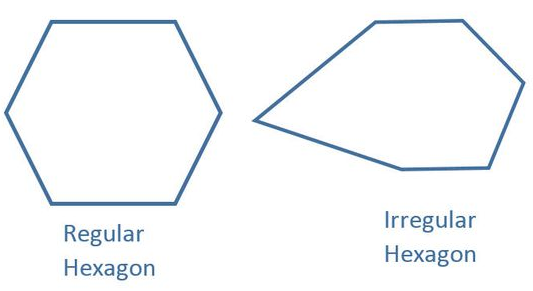
Hexagon:
– A hexagon having all its sides of the same length and equal vertex angles are called a Regular Hexagon.
– An irregular hexagon has unequal sides and angles.
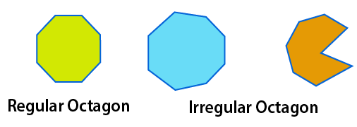
Octagon:
– Regular Octagon: A type of octagon that has all sides and angles equal. Each angle of a regular octagon measures 135° each.
– Irregular Octagon: A type of octagon that has all sides and all angles not equivalent. Angle measurement of an irregular octagon is not similar but remembers that they all sum to 1080°.
Quadrilateral:
A regular quadrilateral is a type of quadrilateral with four sides of equal length and four angles of equal measure. An irregular quadrilateral is a type of quadrilateral having one or more sides of unequal length and one or more angles of unequal measure.
Triangle:
polygons:
– A regular polygon has all its sides equal and all its angles equal in measure. Examples of a regular polygon are square, equilateral triangle, rhombus, etc.
– An irregular polygon does not have all its sides equal and not all the angles are equal in measure. Examples of irregular polygons are scalene triangle, right triangle, isosceles triangle, rectangle, parallelogram, irregular pentagon, irregular hexagon, etc.