All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 7 Multiply Mixed Numbers will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 7 Multiply Mixed Numbers
Math in My World
Example 1
A blueberry muffin recipe calls for \(\frac{1}{2}\) cup of blueberries. A blueberry pie recipe calls for 3\(\frac{1}{2}\) times more blueberries. How many cups of blueberries are needed to make the pie?
1. The model shows \(\frac{1}{2}\) × 3\(\frac{1}{2}\). Shade the squares that represent the product.
How many squares did you shade? _____
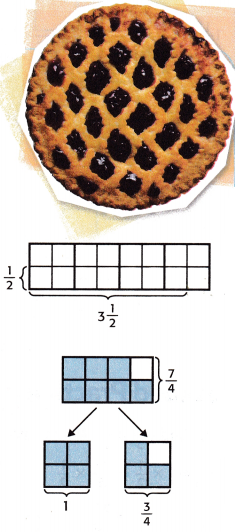
Answer:
The above-given:
1/2 x 3 1/2
3 1/2 = 7/2
Now multiply both the fractions
1/2 x 7/2 = 7/4
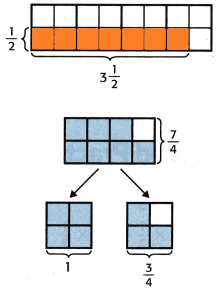
The shaded squares are 7.
2. The shaded squares can be rearranged to form part of the model to the right.
3. Write the product as an improper fraction.
As a mixed number, this is 1\(\frac{3}{4}\)
So, the blueberry pie recipe calls for 
cups of blueberries.
Answer:
The improper fraction is 7/4
Therefore, the blueberry pie recipe calls for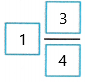 
cups of blueberries.
Key Concept Multiply Mixed Numbers
To multiply mixed numbers, write the mixed numbers as improper fractions. Then multiply as with fractions.
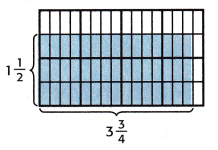
Example 2
Find the unknown in 1\(\frac{1}{2}\) × 3\(\frac{3}{4}\) = 
.
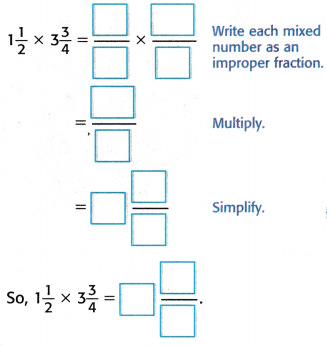
Answer:
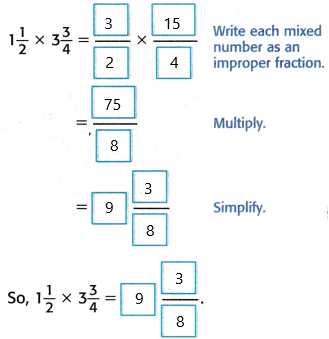
Helpful Hint
To write a mixed number as an improper fraction, multiply the denominator by the whole number and add the numerator. Keep the original denominator.
1\(\frac{1}{2}\) → 2 × 1 + 1 = \(\frac{3}{2}\)
Talk Math
Explain how to find the product of two mixed numbers.
Answer:
Knowing how to multiply fractions will help when it comes to multiplying two mixed numbers. This is because when multiplying mixed numbers, you first have to change them to improper fractions. You then multiply the numerators and denominators, and reduce the results, if possible. Then, in the end, you can change the fraction back to a mixed number.
Guided Practice
Question 1.
Find 4\(\frac{1}{5}\) × \(\frac{1}{2}\). Write in simplest form.
4\(\frac{1}{5}\) × \(\frac{1}{2}\) = \(\frac{21}{5}\) × \(\frac{1}{2}\)
= \(\frac{21}{10}\)
= 
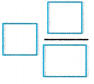
So, 4\(\frac{1}{5}\) × \(\frac{1}{2}\) =
Answer:
The above-given equation:
4 1/5 x 1/2
Now solve the equation.
4 1/5 is a mixed fraction. Now convert it into an improper fraction.
4 1/5 = 21/5
Now multiply the fractions.
21/5 x 1/2 = 21/10
In mixed fractions, we can write as 2 1/10.
Therefore, 4\(\frac{1}{5}\) × \(\frac{1}{2}\) =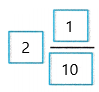 
Independent Practice
Multiply. Write in simplest form.
Question 2.
1\(\frac{1}{3}\) × \(\frac{2}{3}\) = ____
Answer:
The above-given equation:
1 1/3 x 2/3
1 1/3 is a mixed fraction. So convert it into an improper fraction.
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 3 with 1 in the given problem (1 1/3)
3 x 1 = 3
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 3 + 1 = 4
Step 3: Keep the Denominator the same i.e. 3.
Step 4: The Improper fraction obtained is: 4/3
Now we get an improper fraction. And multiply the fractions.
4/3 x 2/3
= 4 x 2/ 3 x 3
= 8/9
In order to simplify a fraction there must be:
1. A number that will divide evenly into both the numerator and denominator so it can be reduced. No such number exists for 8 and 9. (or)
2. The numerator must be greater than the denominator, (an improper fraction), so it can be converted to a mixed number. 8 is not greater than 9.
Therefore, this fraction is in its simplest form.
Question 3.
\(\frac{2}{5}\) × 2\(\frac{3}{4}\) = ____
Answer:
The above-given equation:
2/5 x 2 3/4
2 3/4 is a mixed fraction. So convert it into an improper fraction.
2 3/4 = 11/4
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 4 with 2 in the given problem (2 3/4)
4 x 2 = 8
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 8 + 3 = 11
Step 3: Keep the Denominator the same i.e. 4.
Step 4: The Improper fraction obtained is: 11/3
Now we get an improper fraction. And multiply the fractions.
2/5 x 11/4
= 2 x 11/ 5 x 4
= 22/20
reduce our fraction by dividing both numerator and denominator by it. GCF = 2,
22 ÷2/20 ÷2
= 11/10
Converting to a mixed number using long division with remainders 11÷10
11 ÷ 10 = 1 R1
Therefore,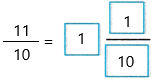 
Question 4.
3\(\frac{3}{5}\) × \(\frac{1}{4}\) = ____
Answer:
The above-given equation:
3 3/5 and 1/4
3 3/5 is a mixed fraction. So convert it into an improper fraction.
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 5 with 3 in the given problem (3 3/5)
5 x 3 = 15
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 15 + 3 = 18
Step 3: Keep the Denominator the same i.e. 5.
Step 4: The Improper fraction obtained is: 18/5
Now we get an improper fraction. And multiply the fractions.
18/5 x 1/4
= 18 x 1/ 5 x 4
= 18/20
reduce our fraction by dividing both numerator and denominator by it. GCF = 2, and getting our simplified answer:
18 ÷ 2/ 20 ÷ 2
= 9/10
Therefore, 3\(\frac{3}{5}\) × \(\frac{1}{4}\) = 9/10
Question 5.
2\(\frac{1}{2}\) × 4\(\frac{1}{5}\) = ____
Answer:
The above-given equation:
2 1/2 x 4 1/5
2 1/2 and 4 1/5 are mixed fractions. So convert it into an improper fraction.
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 2 with 2 in the given problem (2 1/2)
2 x 2 = 4 and for another mixed fraction multiply 4 and 5 (4 1/5) 5 x 4 = 20
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 4 + 1 = 5; 20 + 1 = 21
Step 3: Keep the Denominator the same i.e. 2 and 5.
Step 4: The Improper fraction obtained is: 5/2 and 21/5
Now we get an improper fraction. And multiply the fractions.
5/2 x 21/5
= 5 x 21/ 2 x 5
= 105/10
reduce our fraction by dividing both numerator and denominator by it. GCF = 5,
105 ÷ 5/ 10 ÷ 5
= 21/2
In mixed fractions, we can write: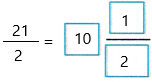 
Question 6.
1\(\frac{1}{3}\) × 3\(\frac{2}{3}\) = ____
Answer:
The above-given equation:
1 1/3 x 3 2/3
1 1/3 and 3 2/3 are mixed fractions. So convert it into an improper fraction.
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 3 with 1 in the given problem (1 1/3)
3 x 1 = 3 and for another mixed fraction multiply 3 and 3 ( 3 2/3) 3 x 3 = 9
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 3 + 1 = 4; 9 + 2 = 11
Step 3: Keep the Denominator the same i.e. 3 and 3.
Step 4: The Improper fraction obtained is: 4/3 and 11/3
Now we get an improper fraction. And multiply the fractions.
4/3 x 11/3
= 4 x 11/ 3 x 3
= 44/9
Converting to a mixed number using long division with remainders 44 ÷ 9
44 ÷ 9 = 4 R8
Therefore,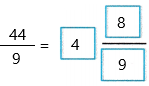 
Question 7.
4\(\frac{2}{5}\) × 1\(\frac{3}{4}\) = ____
Answer:
The above-given equation:
4 2/5 x 1 3/4
4 2/5 and 1 3/4 are mixed fractions. So convert it into an improper fraction.
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 5 with 4 in the given problem (4 2/5)
5 x 4 = 20 and for another mixed fraction, multiply 4 and 1 ( 1 3/4) 4 x 1 = 4
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 20 + 2 = 22; 4 + 3 = 7
Step 3: Keep the Denominator the same i.e. 5 and 4.
Step 4: The Improper fraction obtained is: 22/5 and 5/7
Now we get an improper fraction. And multiply the fractions.
22/5 x 7/4
= 22 x 7/ 5 x 4
= 154/ 20
reduce our fraction by dividing both numerator and denominator by it. GCF = 2,
154 ÷ 2/ 20 ÷ 2
= 77/10
In mixed fractions we can write: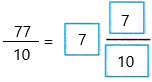 
Question 8.
2\(\frac{4}{5}\) × 6\(\frac{1}{8}\) = ____
Answer:
The above-given equation:
2 4/5 x 6 1/8
2 4/5 and 6 1/8 are mixed fractions. So convert it into an improper fraction.
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 5 with 2 in the given problem (2 4/5)
5 x 2 = 10 and for another mixed fraction, 6 x 8 = 48 ( 6 1/8)
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 10 + 4 = 14 and 48 + 1 = 49
Step 3: Keep the Denominator the same i.e. 5 and 8.
Step 4: The Improper fraction obtained is: 14/5 and 49/8
Now we get an improper fraction. And multiply the fractions.
14/5 x 49/8
= 14 x 49/ 5 x 8
= 686 / 40
reduce our fraction by dividing both numerator and denominator by it. GCF = 2,
686 ÷ 2/ 40 ÷ 2
= 343/20
Converting to a mixed number using long division with remainders for 343 ÷ 20
343 ÷ 20 = 17 R3
Therefore,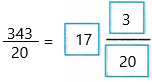 
Question 9.
1\(\frac{5}{6}\) × 4\(\frac{1}{3}\) = ____
Answer:
The above-given equation:
1 5/6 x 4 1/3
1 5/6 and 4 1/3 are mixed fractions. So convert it into an improper fraction.
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 6 with 1 in the given problem (1 5/6)
6 x 1 = 6 and for another mixed fraction, 3 x 4 = 12 ( 4 1/3)
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 6 + 5 = 11 and 12 + 1 = 13
Step 3: Keep the Denominator the same i.e. 6 and 3.
Step 4: The Improper fraction obtained is: 11/5 and 13/3
Now we get an improper fraction. And multiply the fractions.
11/6 x 13/3
= 11 x 13/ 6 x 3
= 143/18
This is a simple fraction.
Converting to a mixed number using long division with remainders for 143 ÷ 18
143 ÷ 18 = 7 R17
Therefore,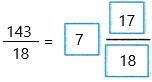 
Question 10.
2\(\frac{3}{5}\) × 3\(\frac{7}{8}\) = ____
Answer:
The above-given equation:
2 3/5 x 3 7/8
2 3/5 and 3 7/8 are mixed fractions. To convert them into an improper fraction.
Mixed fraction to improper fraction:
Step 1: Multiply the denominator with the whole number, i.e. Multiply 5 with 2 in the given problem (2 3/5)
5 x 2 = 10 and for another mixed fraction, the improper fraction will be 8 x 3 = 24 (3 7/8)
Step 2: Add the numerator of the Fraction to the result in step 1. i.e Add 10 + 3 = 13 & 24 + 7 = 31
Step 3: Keep the Denominator the same i.e. 5 and 8.
Step 4: The Improper fraction obtained is: 13/5 and 31/8
Now we get an improper fraction. And multiply the fractions.
13/5 x 31/8
= 13 x 31/ 5 x 8
= 403/40
Converting to a mixed number using long division with remainders for 403 ÷ 40
403 ÷ 40 = 10 R3
Therefore, 403/40 =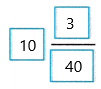 
Algebra Write a multiplication equation represented by each model. Shade the product on the model.
Question 11.
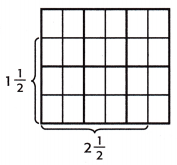
Answer:
A combination of a whole number and a proper fraction is called a mixed fraction.
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Question 12.
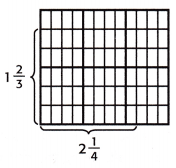
Answer:
A combination of a whole number and a proper fraction is called a mixed fraction.
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Question 13.
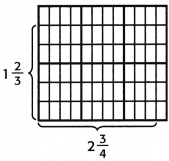
Answer:
A combination of a whole number and a proper fraction is called a mixed fraction.
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Problem Solving
Question 14.
Mathematical PRACTICE 4 Model Math Alexandra made a rectangular quilt that measured 3\(\frac{1}{4}\) feet in length by 2\(\frac{3}{4}\) feet in width. To find the area, multiply the length and width. What is the area of the quilt in square feet? Write an equation to solve.
Answer:
The above-given:
The length of the rectangular quilt = 3 1/4 feet
The width of the rectangular quilt = 2 3/4
we need to find out the area of the rectangle. Let it be A.
The area of the rectangle = length x width
A = 3 1/4 x 2 3/4
Therefore, the area of the rectangle = 8 15/16 square feet.
Question 15.
Laney bought 1\(\frac{2}{3}\) pounds of grapes. She also bought bananas that were 2\(\frac{1}{4}\)– times the weight of the grapes. How much did the bananas weigh?
Answer:
The above-given:
The number of pounds of grapes Laney bought = 1 2/3
The bananas she bought that were the weight of the grapes = 2 1/4
The weight of bananas = W
W = 1 2/3 x 2 1/4
Now convert the mixed fractions into improper fractions.
W = 5/3 x 9/4
W = 5 x 9/ 3 x 4
W = 45/12
reduce our fraction by dividing both numerator and denominator by it. GCF = 3,
45 ÷ 3/ 12 ÷ 3
= 15/4
In mixed fractions, we can write as 3 3/4
Therefore, the weight of bananas is 3 3/4 pounds.
Question 16.
Mrs. Plesich has a 16\(\frac{1}{2}\) ounce bag of chocolate chips. She will only use \(\frac{1}{4}\) of the bag for decorating a cake. How many ounces will she use for decorating?
Answer:
The above-given:
The bag of chocolate chips Mrs Plesich has = 16 1/2 ounce
The chips she used for decorating the chocolate cake = 1/4
The number of ounces she used for decorating = O
O = 16 1/2 x 1/4
16 1/2 is a mixed fraction. Convert it into an improper fraction.
16 1/2 = 16 x 2/2 + 1/2 = 32/2 + 1/2 = 33/2
Now multiply the fractions:
O = 33/2 x 1/4
O = 33 x 1/ 2 x 4
O = 33/8
In mixed fractions, we can write as 33/8 = 4 1/8
Therefore, she uses 4 1/8 ounces of chocolate chips to decorate a cake.
HOT Problems
Question 17.
Mathematical Practice 2 Use Number Sense Write and solve a real-world problem that involves finding the product of a fraction and a mixed number.
Answer:
Jasp spent 2/3 of the 2 1/2 working hours mowing. How much time did he spend on mowing?
Let the time he spends on mowing be ‘T’
T = 2/3 x 2 1/2
2 1/2 is a mixed fraction. Convert it into improper fractions.
2 1/2 = 2 x 2/2 + 1/2 = 4/2 + 1/2 = 5/2
T = 2/3 x 5/2
T= 2 x 5/ 3 x 2
T = 10/6
reduce our fraction by dividing both numerator and denominator by it. GCF = 2,
T = 10 ÷ 2/ 6 ÷ 2
T = 5/3
In mixed fractions, we can write as 5/3 = 1 2/3
Therefore, he spent 1 2/3 hours mowing.
Question 18.
? Building on the Essential Question How is multiplying mixed numbers different from multiplying fractions?
Answer:
When multiplying a regular fraction there is no whole number in front of it so all you would do is multiply the fractions. But a mixed number does have a whole number in front of it so you would multiply the fraction part the exact same way it’s just after the end you would have to add the whole numbers in front of each fraction together.
(or)
In order to multiply mixed numbers, I need to change the mixed number to the improper fractions first. Then I can multiply as I do with fractions.
McGraw Hill My Math Grade 5 Chapter 10 Lesson 7 My Homework Answer Key
Multiply. Write in the simplest form.
Question 1.
5\(\frac{1}{3}\) × 1\(\frac{1}{4}\) = ____
Answer:
A combination of a whole number and a proper fraction is called a mixed fraction.
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
Question 2.
1\(\frac{2}{5}\) × 3\(\frac{1}{6}\) = ____
Answer:
A combination of a whole number and a proper fraction is called a mixed fraction.
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
Question 3.
7\(\frac{1}{8}\) × 2\(\frac{5}{6}\) = ____
Answer:
A combination of a whole number and a proper fraction is called a mixed fraction.
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
Problem Solving
Question 4.
The table shows some ingredients in lasagna. If you make three times the recipe, how many cups of cheese are needed?
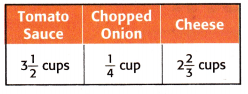
Answer:
The above-given:
The cheese = 2 2/3 cups
now convert it into a fraction
2 2/3 = 8/3
If we want to make three cups then the equation will be:
C = 8/3 x 3
C = 24/3
C = 8
Therefore, 8 cups of cheese is needed.
Question 5.
Karyn purchased a square picture frame. Each side measures 1\(\frac{1}{4}\) feet. What is the area of the picture frame in square feet?
Answer:
The area of square = a x a
The above-given side: 1 1/4
Now convert the mixed fraction into a fraction
1 1/4 = 5/4
The area of the picture frame = A
A = 5/4 x 5/4
X = 25/16
Therefore, the area of the picture frame is 25/16 square feet.
Question 6.
It takes Marty 1\(\frac{1}{4}\) hours to get ready for school. If \(\frac{1}{5}\) of that time is used to shower, what fraction of an hour does it take him to shower?
Answer:
The above-given:
The number of hours to get ready for school = 1 1/4 = 5/4
The time used for shower = 1/5
The fraction of an hour it take him to shower = S
S = 5/4 x 1/5
S = 5/20
S = 1/4
Therefore, 1/4 of an hour he takes for the shower.
Question 7.
Mathematical PRACTICE 2 Use Algebra Kallisto built a rectangular sign that measured 2\(\frac{3}{4}\) feet in length by 1\(\frac{1}{2}\) feet in width. To find the area, multiply the length and width. What is the area of the sign in square feet? Write an equation to solve.
Answer:
The length of the rectangular sign = 2 3/4 = 11/4
The width of the rectangular sign = 1 1/2 = 3/2
The area of the sign = A
The area of the rectangle = length x width
A = 11/4 x 3/2
A = 33/8
Therefore, the area of the rectangle is 33/8 square feet.
Test Practice
Question 8.
Antoinette bought 2\(\frac{2}{3}\) pounds of grapes. If she bought bananas that weighed 1\(\frac{1}{4}\) times as much as the grapes, how much did the bananas weigh?
A. 2\(\frac{1}{6}\) pounds
B. 3\(\frac{1}{3}\) pounds
C. 3\(\frac{1}{4}\) pounds
D. 3\(\frac{1}{2}\) pounds
Answer: Option B is correct.
The above-given:
The number of pounds of grapes he bought = 2 2/3 = 8/3
The weight of bananas as much as grapes = 1 1/4 = 5/4
The weight of bananas = W
W = 8/3 x 5/4
W = 40/12
reduce our fraction by dividing both numerator and denominator by it. GCF = 4,
W = 10/3
Converting to a mixed number using long division with remainders for 10 ÷ 3
10 ÷ 3 = 3 R1
The mixed fraction is 3 1/3.