All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 6 Multiply Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 6 Multiply Fractions
Math in My World
Example 1
Franco ate some pizza. Two-thirds of a pizza is left. Diandra ate \(\frac{3}{4}\) of the leftover pizza. How much of a whole pizza did Diendra eat?
Find \(\frac{3}{4}\) of \(\frac{2}{3}\) ← \(\frac{3}{4}\) of \(\frac{2}{3}\) is the same as \(\frac{3}{4}\) × \(\frac{2}{3}\)
One Way Multiply first. Then simplify.
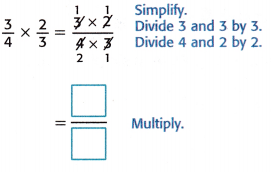
\(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{3 \times 2}{4 \times 3}\)
= \(\frac{6}{12}\) Multiply
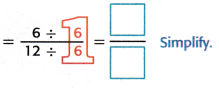
Another Way Simplify first.
So, Diandra ate ![]() of the whole pizza.
of the whole pizza.
Answer:
The above-given:
The amount of pizza left = 2/3
The amount of pizza Diandra ate from the leftover pizza = 3/4
The amount of whole pizza did Diandra ate = P
P = 2/3 x 3/4
P = 2 x 3/ 3 x 4
P = 6/12
P = 1/2
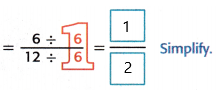
Another simplification:
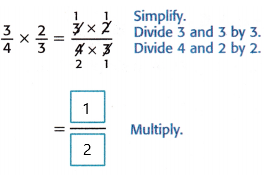
Therefore, Diandra ate 1/2 of the whole pizza.
To find the area of a rectangle, multiply the length and the width.
Example 2
Find the area of the rectangle with a length of \(\frac{3}{4}\) inch and a width of \(\frac{5}{9}\) inch.
One Way Tile the rectangle as part of a unit square.
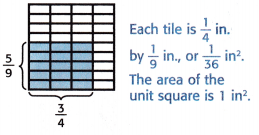
Count the shaded tiles.
There are 15 tiles shaded.
15 × \(\frac{1}{36}\) = \(\frac{15}{36}\)
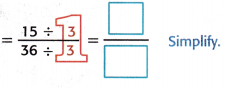
So, the area of the rectangle is  square inch.
square inch.
Another Way Multiply the side lengths.
\(\frac{3}{4}\) × \(\frac{5}{9}\) = \(\frac{3 \times 5}{4 \times 9}\)
= \(\frac{15}{36}\) Multiply
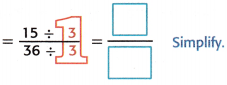
Answer:
The length of the rectangle = 3/4
The width of the rectangle = 5/9
The area of the rectangle = A
A = 3/4 x 5/9
One method
– Counting the number of tiles that are shaded.
The number of tiles shaded = 15
15 x 1/36 = 15/36
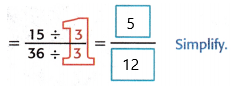
so, the area of the rectangle is 5/12 square inches.
Another Way Multiply the side lengths.
3/4 x 5/9
= 3 x 5/ 4 x 9
= 15/36
= 5/12

Talk Math
Will the product of \(\frac{2}{9}\) × \(\frac{1}{3}\) be the same as the product of
\(\frac{2}{6}\) × \(\frac{2}{6}\)? Explain.
Answer:
The above-given equation:
2/9 x 1/3
= 2 x 1/ 9 x 3
= 2/27
Another equation:
2/6 x 2/6
= 2 x 2/ 6 x 6
= 4/36
if we divide with 2
= 2/19
Therefore, both products are not the same.
Guided Practice
Question 1.
Find \(\frac{1}{7}\) × \(\frac{1}{2}\). Write in simplest form.
\(\frac{1}{7}\) × \(\frac{1}{2}\) = \(\frac{1 \times 1}{7 \times 2}\)
= 
So, \(\frac{1}{7}\) × \(\frac{1}{2}\) = 
Answer:
The above-given equation:
1/7 x 1/2
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
this can be simplified as:
= 1/14
Therefore, 1/7 x 1/2 = 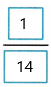
Independent Practice
Shade the models to find each product. Write in simplest form.
Question 2.
\(\frac{5}{6}\) × \(\frac{3}{4}\) = ____

Answer:
The above-given equation:
5/6 x 3/4
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
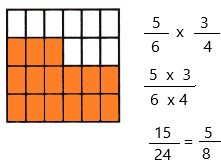
Divide the square into 4 equal rows since the denominator of the fraction is 4.
Divide the square into 6 equal columns since the denominator of the fraction is 6.
Therefore, out of 24 sections, we shaded 15 portions
Question 3.
\(\frac{3}{10}\) × \(\frac{5}{6}\) = ____

Answer:
The above-given equation:
3/10 x 5/6
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
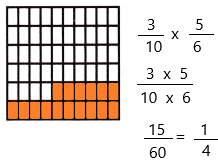
Divide the square into 6 equal rows since the denominator of the fraction is 6.
Divide the square into 10 equal columns since the denominator of the fraction is 10.
Therefore, out of 60 sections, we shaded 15 portions.
Question 4.
\(\frac{3}{4}\) × \(\frac{2}{7}\) = ____
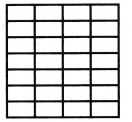
Answer:
The above-given equation:
3/4 x 2/7
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
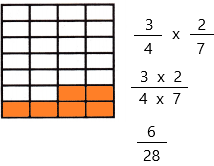
Divide the square into 6 equal rows since the denominator of the fraction is 6.
Divide the square into 4 equal columns since the denominator of the fraction is 4.
Therefore, out of 28 sections, we shaded 6 portions.
Multiply. Write in the simplest form.
Question 5.
\(\frac{3}{5}\) × \(\frac{5}{6}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Rules to find the simplest form of a fraction:
Let the given fraction be a/b and the HCF of a and b be h. Then, a/b = a ÷ h/b ÷ h is the simplest form.
The above-given equation:
3/5 x 5/6
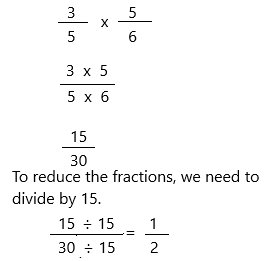
Therefore, \(\frac{3}{5}\) × \(\frac{5}{6}\) = 1/2
Question 6.
\(\frac{3}{4}\) × \(\frac{5}{12}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Rules to find the simplest form of a fraction:
Let the given fraction be a/b and the HCF of a and b be h. Then, a/b = a ÷ h/b ÷ h is the simplest form.
The above-given equation:
3/4 x 5/12

Therefore, \(\frac{3}{4}\) × \(\frac{5}{12}\) = 5/16
Question 7.
\(\frac{2}{9}\) × \(\frac{1}{3}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Rules to find the simplest form of a fraction:
Let the given fraction be a/b and the HCF of a and b be h. Then, a/b = a ÷ h/b ÷ h is the simplest form.
The above-given equation:
2/9 x 1/3
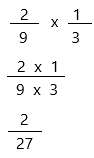
In order to simplify a fraction there must be:
1. A number that will divide evenly into both the numerator and denominator so it can be reduced. No such number exists for 2 and 27. (or)
2. The numerator must be greater than the denominator, (an improper fraction), so it can be converted to a mixed number. 2 is not greater than 27.
Therefore, This fraction is in its simplest form: 2/27
Question 8.
\(\frac{3}{4}\) × \(\frac{2}{5}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Rules to find the simplest form of a fraction:
Let the given fraction be a/b and the HCF of a and b be h. Then, a/b = a ÷ h/b ÷ h is the simplest form.
The above-given equation:
3/4 x 2/5

Therefore, \(\frac{3}{4}\) × \(\frac{2}{5}\) = 3/10
Question 9.
\(\frac{1}{3}\) × \(\frac{2}{5}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Rules to find the simplest form of a fraction:
Let the given fraction be a/b and the HCF of a and b be h. Then, a/b = a ÷ h/b ÷ h is the simplest form.
The above-given equation:
1/3 x 2/5
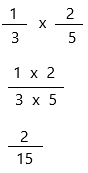
In order to simplify a fraction there must be:
1. A number that will divide evenly into both the numerator and denominator so it can be reduced. No such number exists for 2 and 15. (or)
2. The numerator must be greater than the denominator, (an improper fraction), so it can be converted to a mixed number. 2 is not greater than 15.
This fraction is in its simplest form: 2/15
Question 10.
\(\frac{3}{5}\) × \(\frac{5}{7}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Rules to find the simplest form of a fraction:
Let the given fraction be a/b and the HCF of a and b be h. Then, a/b = a ÷ h/b ÷ h is the simplest form.
The above-given equation:
3/5 x 5/7
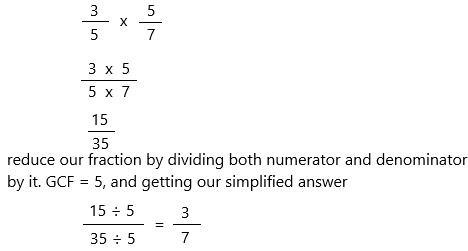
Therefore, \(\frac{3}{5}\) × \(\frac{5}{7}\) = 3/7
Algebra Find the unknown in each equation. Write in the simplest form.
Question 11.
\(\frac{6}{7}\) × \(\frac{3}{4}\) = x
x = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
Rules to find the simplest form of a fraction:
Let the given fraction be a/b and the HCF of a and b be h. Then, a/b = a ÷ h/b ÷ h is the simplest form.
The above-given equation:
x = 6/7 x 3/4
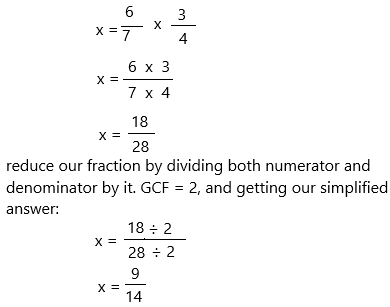
Therefore, \(\frac{6}{7}\) × \(\frac{3}{4}\) = 9/14
Question 12.
\(\frac{2}{3}\) × \(\frac{1}{4}\) = m
m = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
m = 2/3 x 1/4
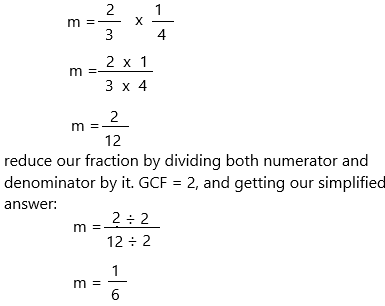
Therefore, m = 1/6.
Question 13.
\(\frac{5}{6}\) × \(\frac{2}{3}\) = p
p = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
p = 5/6 x 2/3

Therefore, \(\frac{5}{6}\) × \(\frac{2}{3}\) = 5/9.
Problem Solving
Question 14.
Algebra Find the area of the rectangle shown. Write an equation.
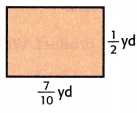
Answer:
The area of rectangle = length x breadth
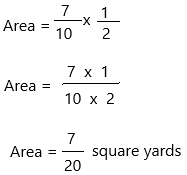
Therefore, the area of the rectangle is 7/20 square yards.
Question 15.
Mathematical PRACTICE 7 Identify Structure Refer to Example 1. Complete the steps to show how \(\frac{3}{4}\) × \(\frac{2}{3}\) can also be found using properties and equivalent fractions.
\(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{3 \times 2}{4 \times 3}\) Multiply numerators.
Multiply denominators.
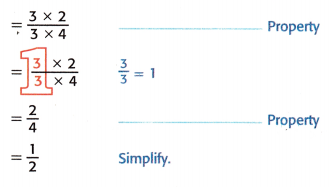
Answer:
Commutative property: The commutative property deals with the arithmetic operations of addition and multiplication. It means that changing the order or position of two numbers while adding or multiplying them does not change the end result.
Formula:
If two numbers A and B are given, then the formula of the commutative property of numbers is given as,
1. A + B = B + A
2. A x B = B x A
3. A – B ≠ B – A
4. A ÷ B ≠ B ÷ A
Identity property: An identity element is a number that, when used in an operation with another number, results in the same number. The additive and multiplicative identities are two of the earliest identity elements people typically come across; the additive identity is 0 and the multiplicative identity is 1.
HOT Problems
Question 16.
Mathematical PRACTICE 4 Model Math Write a real-world problem that describes the model.
Answer:
The real-world problem would be:
Neeru hiked a trail that is 1/4 mile each way. After hiking 1/4 of the trail, he stopped to rest. What fraction of a mile did Neeru hike before he stopped to rest?
To solve this we need to form an equation:
F = 1/4 x 1/4
F = 1/16
The model can be described as:
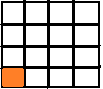
Therefore, out of 16 sections, 1 potion is shaded.
Question 17.
? Building on the Essential Question How can I multiply fractions?
Answer:
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
– Multiplying fractions is not like the addition or subtraction of fractions, where the denominators of both fractions should be the same. Two fractions can be multiplied easily, even if the denominators are different. While multiplying fractions, it should be kept in mind that the fractions can be in a proper fraction or improper fraction, but they cannot be mixed fractions.
Multiplying fractions is defined as the product of a fraction with a fraction or with an integer or with the variables. The procedure to multiply the fractions are:
– Multiply the numerator with the numerator
– Multiply the denominator with the denominator
– Simplify the fractions, if required
McGraw Hill My Math Grade 5 Chapter 10 Lesson 6 My Homework Answer Key
Practice
Multiply. Write in the simplest form.
Question 1.
\(\frac{4}{9}\) × \(\frac{3}{8}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
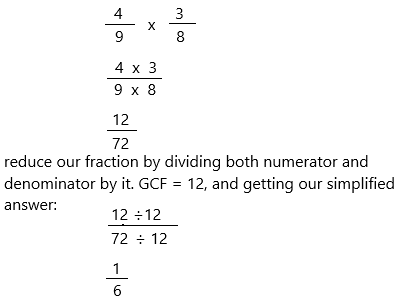
Question 2.
\(\frac{3}{4}\) × \(\frac{5}{8}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
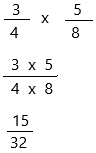
Question 3.
\(\frac{1}{8}\) × \(\frac{3}{4}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
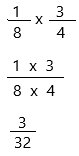
The fraction is in its simplest form: 3/32
Question 4.
\(\frac{3}{5}\) × \(\frac{1}{3}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:

Question 5.
\(\frac{5}{7}\) × \(\frac{1}{4}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:
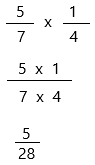
Question 6.
\(\frac{7}{8}\) × \(\frac{2}{9}\) = ____
Answer:
Finding the simplest form of any fraction is a simple process. We need to simplify the fraction’s numerator and denominator by dividing them both by the biggest common factor that divides them entirely. Both the numerator and denominator should be entire integers after division. This approach of fractional simplification is also known as reducing fractions.
The above-given equation:

Problem Solving
Algebra Write an equation to solve Exercises 7 and 8.
Question 7.
Carrie ate some of the oranges that her mother brought home from the grocery store. Of the
oranges her mother bought, \(\frac{1}{4}\) were left over. Shyla, Carrie’s sister, ate \(\frac{2}{5}\) of the oranges that were left over. What fraction of the oranges did Shyla eat?

Answer:
The number of oranges left over = 1/4
The number of oranges eaten = 2/5
The fraction of oranges = O
O = 1/4 x 2/5
O = 2/20
O = 1/10.
Therefore, the fraction of oranges Shyla eat is 1/10.
Question 8.
Find the area of the rectangle shown.
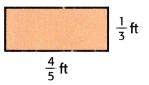
Answer:
The area of rectangle = length x breadth
A = 4/5 x 1/3
A = 4/15
Therefore, the area of a rectangle = 4/15 square ft.
Question 9.
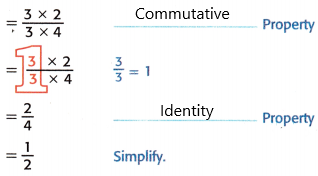
Mathematical PRACTICE 7 Identify Structure Complete the steps to show how \(\frac{4}{5}\) × \(\frac{5}{6}\) can also be found using properties and equivalent fractions.
\(\frac{4}{5}\) × \(\frac{5}{6}\) = \(\frac{4 \times 5}{5 \times 6}\) Multiply numerators.
Multiply denominators.
= \(\frac{5 \times 4}{5 \times 6}\) _____ Property
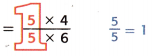
= \(\frac{4}{6}\) ____ Property
= \(\frac{2}{3}\) Simplify.
Answer:
Commutative property: The commutative property deals with the arithmetic operations of addition and multiplication. It means that changing the order or position of two numbers while adding or multiplying them does not change the end result.
Formula:
If two numbers A and B are given, then the formula of the commutative property of numbers is given as,
1. A + B = B + A
2. A x B = B x A
3. A – B ≠ B – A
4. A ÷ B ≠ B ÷ A
Identity property: An identity element is a number that, when used in an operation with another number, results in the same number. The additive and multiplicative identities are two of the earliest identity elements people typically come across; the additive identity is 0 and the multiplicative identity is 1.
5/4 x 5/6
= commutative property
5/5 = 1
It is an identity property.
Test Practice
Question 10.
James made flashcards for \(\frac{5}{6}\) of the vocabulary words. Lauretta made \(\frac{1}{2}\) of the number of cards that James made. What fraction of the vocabulary words did Lauretta make cards for?
A. \(\frac{5}{12}\)
B. \(\frac{1}{2}\)
C. \(\frac{7}{12}\)
D. \(\frac{3}{4}\)
Answer: Option A is correct.
The above-given:
The number of flashcards = 5/6
The number of flashcards Lauretta made = 1/2
The fraction of the vocabulary words = L
L = 5/6 x 1/2
L = 5/12
Therefore, the Lauretta make cards are 5/12