All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 5 Use Models to Multiply Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 5 Use Models to Multiply Fractions
Draw It
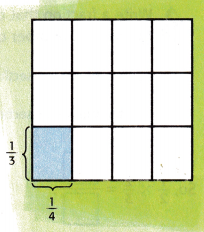
Find \(\frac{1}{3}\) × \(\frac{1}{4}\). Write in simplest form.
To find \(\frac{1}{3}\) × \(\frac{1}{4}\), find the area of a \(\frac{1}{3}\)– by \(\frac{1}{4}\)-unit rectangle
1. Divide the square into ____ equal rows since the denominator of the first fraction is 3.
Answer:
The above-given fractions:
1/3 and 1/4
already representation is given in the below square.
as per first fraction 1/3.
We divide the square into 3 equal rows since the denominator of the first fraction is 3.
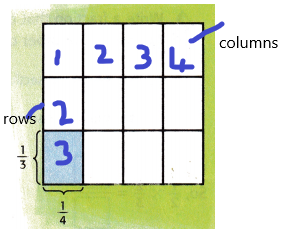
2. Divide the square into ___ equal columns since the denominator of the second fraction is 4
Answer:
According to the above-given square:
The fraction for the columns is 1/4.
So we divide the square into 4 equal columns since the denominator of the fraction is 4.
3. Shade the portion of the model where \(\frac{1}{3}\) and \(\frac{1}{4}\) intersect
How many sections of the model are shaded? ______
Answer:
There are 12 sections in the model.
We need to shade the single portion of the model.
The calculation of fraction is:
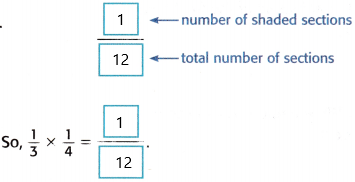
1/3 x 1/4 = 1/12
so out of 12 sections, we need to shade 1 portion of the model.
4. Write a fraction that compares the number of shaded sections to the total number of sections.
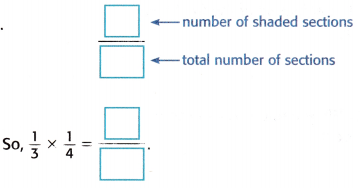
Answer:
The fraction that compares the number of shaded sections to the total number of sections.
Try It
Find \(\frac{1}{2}\) × \(\frac{2}{3}\). Write in simplest form.
To find \(\frac{1}{2}\) × \(\frac{2}{3}\), find the area of a \(\frac{1}{2}\)– by \(\frac{2}{3}\)-unit rectangle.
1. Divide the square into ____ equal rows since the denominator of the first fraction is 2.
Answer:
The above-given fractions:
1/2 and 2/3
already representation is given in the below square.
as per first fraction 1/2.
We divide the square into 2 equal rows since the denominator of the first fraction is 2.
2. Divide the square into ___ equal columns since the denominator of the second fraction is 3.
Answer:
According to the below-given square:
The fraction for the columns is 2/3.
So we divide the square into 3 equal columns since the denominator of the fraction is 3.
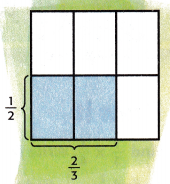
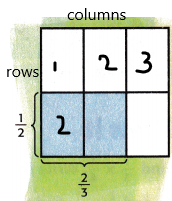
3. Shade the portion of the model where \(\frac{1}{2}\) and \(\frac{2}{3}\) intersect. How many sections of the model are shaded? _____
Answer:
The above-given fractions:
1/2 and 2/3
out of 6 sections, 2 portions were shaded.
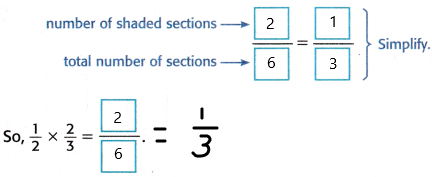
4. Write a fraction that compares the number of shaded sections to the total number of sections. Simplify the fraction.
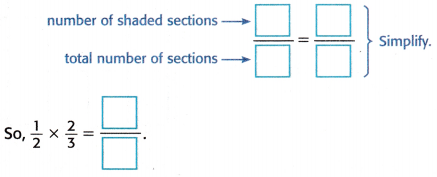
Answer:
the number of shaded sections to the total number of sections
Talk About It
Question 1.
In the second activity, how do the numerators of the fractions \(\frac{1}{2}\) and \(\frac{2}{3}\) relate to the total number of shaded sections, 2?
Answer:
If we calculate the fractions then we get to know that they are relatable.
Calculate the fractions and then we get the product. Let it be P
P = 1/2 x 2/3
P = 1 x 2/ 2 x 3
P = 2/6 {here out of 6 sections, 2 portions were shaded}
P = 1/3
Question 2.
In the second activity, how do the denominators of the fractions relate to the total number of sections, 6?
Answer:
The fractions, 1/2 and 2/3
1/2 x 2/3
then we get 2/6
since the value of the denominator is 6 we divide the square into 6 equal sections.
Question 3.
Mathematical PRACTICE 2 stop and Reflect Write a rule you can use to multiply fractions without using models.
Answer:
Multiplying fractions is defined as the product of a fraction with a fraction or with an integer or with the variables. The procedure to multiply the fractions are:
– Multiply the numerator with the numerator
– Multiply the denominator with the denominator
– Simplify the fractions, if required
Practice It
Mathematical PRACTICE 5 Use Math Tools Shade the models to find each product. Write in simplest form.
Question 4.
\(\frac{1}{6}\) × \(\frac{2}{3}\) = _____

Answer:
The above-given equation:
1/6 x 2/3
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 6 equal rows since the denominator of the first fraction is 6
Divide the square into 3 equal columns since the denominator of the second fraction is 3
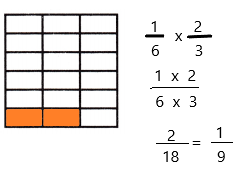
Therefore, out of 18 sections, 2 portions were shaded.
Question 5.
\(\frac{3}{5}\) × \(\frac{1}{3}\) = _____
Answer:
The above-given equation:
3/5 x 1/3
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 5 equal rows since the denominator of the first fraction is 5
Divide the square into 3 equal columns since the denominator of the second fraction is 3
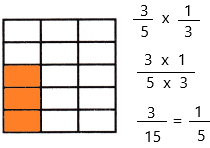
Therefore, out of 15 sections, 3 portions were shaded.
Question 6.
\(\frac{3}{4}\) × \(\frac{1}{6}\) = _____

Answer:
The above-given equation:
3/4 x 1/6
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 4 equal rows since the denominator of the first fraction is 4
Divide the square into 6 equal columns since the denominator of the second fraction is 6
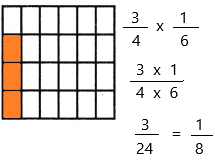
Therefore, out of 24 sections, we shaded 3 portions.
Question 7.
\(\frac{3}{5}\) × \(\frac{3}{4}\) = _____
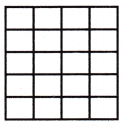
Answer:
The above-given equation:
3/5 x 3/4
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 5 equal rows since the denominator of the first fraction is 5
Divide the square into 4 equal columns since the denominator of the second fraction is 4
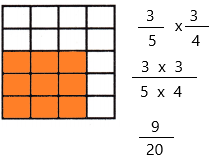
Therefore, out of 20 sections, we shaded 9 portions.
Question 8.
\(\frac{3}{5}\) × \(\frac{1}{5}\) = _____

Answer:
The above-given equation:
3/5 x 1/5
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 5 equal rows since the denominator of the first fraction is 5
Divide the square into 5 equal columns since the denominator of the second fraction is 5
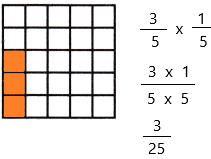
Therefore, out of 25 sections, we shaded 3 portions
Question 9.
\(\frac{1}{2}\) × \(\frac{3}{5}\) = _____

Answer:
The above-given equation:
1/2 x 3/5
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 2 equal rows since the denominator of the first fraction is 2
Divide the square into 5 equal columns since the denominator of the second fraction is 5
Therefore, out of 10 sections, we shaded 3 portions.
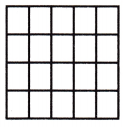
Question 11.
\(\frac{3}{4}\) × \(\frac{2}{5}\) = _____
Answer:
The above-given equation:
3/4 x 2/5
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 4 equal rows since the denominator of the first fraction is 4
Divide the square into 5 equal columns since the denominator of the second fraction is 5
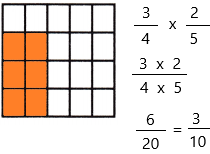
Therefore, out of 20 sections, we shaded 6 portions.
Question 12.
\(\frac{2}{3}\) × \(\frac{2}{3}\) = _____

Answer:
The above-given equation:
2/3 x 2/3
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 3 equal rows since the denominator of the first fraction is 3
Divide the square into 3 equal columns since the denominator of the second fraction is 3
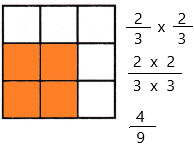
Therefore, out of 9 sections, we shaded 4 portions.
Apply It
Question 12.
Mathematical PRACTICE 5 Use Math Tools Ruby biked a trail that is \(\frac{3}{5}\) mile each way. After biking \(\frac{1}{4}\) of the trail, she stopped to rest. What fraction of a mile did Ruby bike before she stopped to rest? Use models to help you solve.
Answer:
The above-given:
The number of miles Ruby biked a trail = 3/5
The number of miles after she stopped for rest = 1/4
The number of miles she biked before she stopped for rest = M
M = 3/5 x 1/4
M = 3/20
The model can be represented as:

Divide the square into 5 equal rows since the denominator of the first fraction is 5
Divide the square into 4 equal columns since the denominator of the second fraction is 4.
Therefore, out of 20 sections, we shaded 3 portions.
Question 13.
On Saturday, Tom spent \(\frac{1}{3}\) of the day preparing snacks and decorating for a birthday party. Tom spent \(\frac{3}{8}\) of this time decorating the cake. What fraction of the day did Tom spend decorating the cake? Use models to help you solve.

Answer:
The day Tom spent preparing snacks and decorating = 1/3
The day Tom spent decorating the cake = 3/8
The fraction of the day Tom spend decorating the cake = D
D = 1/3 x 3/8
D = 3/24
D = 1/8
The model can be represented as:
Divide the model into 3 equal rows since the denominator of the first fraction is 3
Divide the square into 8 equal columns since the denominator of the second fraction is 8.
Therefore, out of 24 sections, we shaded 3 portions.
Question 14.
Mathematical PRACTICE 4 Model Math Write a real-world problem that could be represented by the model. Then solve.

Answer:
On Sunday, Neeru spent \(\frac{2}{3}\) of the day preparing snacks and decorating for a birthday party. Neeru spent \(\frac{3}{5}\) of this time decorating the cake. What fraction of the day did Tom spend decorating the cake?
If we solve the problem:
2/3 x 3/5
= 2 x 3/ 3 x 5
= 6/15 = 2/5
The above-given square also out of 15 sections, 6 portions are shaded.
Write About It
Question 15.
How can I use models to multiply fractions?
Answer:
1. Draw a big rectangle or square.
2. Divide it into as many equal horizontal strips as the denominator of the first fraction. Shade parts to represent the first fraction.
3. Next, divide the same model into as many equal vertical strips as the denominator of the second fraction. Shade parts to represent the second fraction.
4. Identify the overlapping part in the model. The fraction it represents is the product of the two fractions.
McGraw Hill My Math Grade 5 Chapter 10 Lesson 5 My Homework Answer Key
Practice
Shade the models to find each product. Write in simplest form.
Question 1.
\(\frac{1}{2}\) × \(\frac{1}{2}\) = _____

Answer:
The above-given equation:
1/2 x 1/2
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 2 equal rows since the denominator of the first fraction is 2
Divide the square into 2 equal columns since the denominator of the second fraction is 2
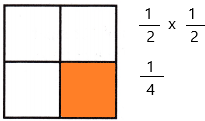
Therefore, out of 4 sections, 1 portion was shaded.
Question 2.
\(\frac{4}{5}\) × \(\frac{1}{2}\) = _____
Answer:
The above-given equation:
4/5 x 1/2
When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, that a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively.
Divide the square into 5 equal rows since the denominator of the first fraction is 5
Divide the square into 2 equal columns since the denominator of the second fraction is 2
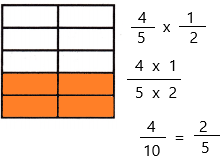
Therefore, out of 10 sections, 4 portions were shaded.
Problem Solving
Draw models to help you solve Exercises 3-7.
Question 3.
Charlotte spent \(\frac{1}{2}\)– of the day shopping at the mall. She spent \(\frac{1}{4}\) of this time trying on jeans. What fraction of the day did Charlotte spend trying on jeans?
Answer:
The above-given:
The day he spent shopping = 1/2
The time he spent trying on jeans = 1/4
The fraction of the day he spends trying on jeans = T
T = 1/2 x 1/4
T = 1/8
The model can be represented as:
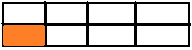
Divide the square into 2 equal rows since the denominator of the first fraction is 2
Divide the square into 4 equal columns since the denominator of the second fraction is 4
Question 4.
Ms. Hendricks is buying a rectangular piece of land that is \(\frac{2}{5}\) mile on one side and \(\frac{5}{6}\) mile on an adjacent side. What is the area of the piece of land?
Answer:
The above-given:
The mile on one side in a rectangular piece of land = 2/5
The mile on the adjacent side in a rectangular piece of land = 5/6
The area of the piece of land = A
A = 2/5 x 5/6
A = 2 x 5/ 5 x 6
A = 10/30
A = 1/3
The model can be represented as:
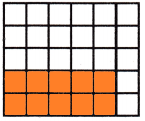
Divide the square into 5 equal rows since the denominator of the first fraction is 5
Divide the square into 6 equal columns since the denominator of the second fraction is 6
Therefore, out of 30, we shaded 10 portions.
Question 5.
Katenka cross country skied a trail that was \(\frac{3}{4}\) mile each way. After skiing \(\frac{2}{3}\) of the trail, she turned around. What fraction of a mile did Katenka ski before she turned around?
Answer:
The above-given:
The mile he skied a trail = 3/4
The mile after she turned around = 2/3
The fraction of the mile did Katenka ski before she turned around = S
S = 3/4 x 2/3
S = 6/12
S = 1/2
The model can be represented as:

Divide the square into 4 equal rows since the denominator of the first fraction is 4
Divide the square into 3 equal columns since the denominator of the second fraction is 3
Therefore, out of 12, we shaded 6 portions.
Question 6.
Mathematical PRACTICE 5 Use Math Tools Merriam spent \(\frac{3}{4}\) of her allowance at the mall. Of the money spent at the mall, \(\frac{1}{3}\) was spent on new earrings. What part of her allowance did Merriam spend on earrings?
Answer:
The above-given:
The amount spent on the mall = 3/4
The amount spent on new earrings = 1/3
The part of her allowance did Merriam spend on earrings = A
A = 3/4 x 1/3
A = 3/12
A = 1/4
Therefore, she spent 1/4 of her allowance.
The model can be represented as:
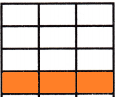
Divide the square into 4 equal rows since the denominator of the first fraction is 4
Divide the square into 3 equal columns since the denominator of the second fraction is 3
Therefore, out of 12, we shaded 3 portions.
Question 7.
Lexi ate some of the apples that her mother brought home from the farmer’s fair. One-half of the apples
were left over. Starr ate \(\frac{1}{6}\) of the apples that were

Answer:
The above-given:
The amount of apple left over = 1/2
The amount of apple = 1/6
1/2 x 1/6
= 1/12
The model can be represented as:
![]()
Divide the square into 2 equal rows since the denominator of the first fraction is 2
Divide the square into 6 equal columns since the denominator of the second fraction is 6
Therefore, out of 12, we shaded 1 portion.