All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 4 Multiply Whole Numbers and Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 4 Multiply Whole Numbers and Fractions
Math in My World
Example 1
Wild parrots spend \(\frac{1}{6}\) of the day looking for food. How many hours a day does a parrot spend looking for food?

Find \(\frac{1}{6}\) × 24. ← There are 24 hours in a
\(\frac{1}{6}\) × 24 = \(\frac{1}{6}\) × \(\frac{24}{1}\) Write 24 as a fraction.
\(\frac{1 \times 24}{6 \times 1}\) ← Multiply the numerators
← Multiply the denominators
= \(\frac{24}{6}\) or _____ Simplify
So, a wild parrot spends _____ hours a day looking for food.
Check \(\frac{1}{6}\) × 24 = 1 × 24 ÷ 6, or _____
Answer:
The day a wild parrot can spend looking for food = 1/6.
The number of hours in a day = 24.
We need to find out the time. Let it be H.
H = 1/6 x 24
Now write 24 as a fraction.
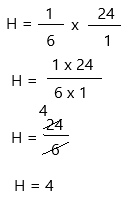
Therefore, a wild parrot spends 4 hours looking for food.
Key Concept Multiply Fractions
To multiply a whole number by a fraction, write the whole number as a fraction. Then multiply the numerators and multiply the denominators.
Example 2
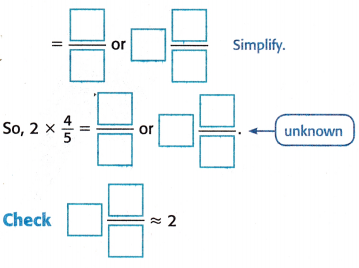
Find the unknown in 2 × \(\frac{4}{5}\) = ![]() .
.
Estimate 2 × 1 = ___2_
Helpful Hint
Multiplication is commutative.
2 × \(\frac{4}{5}\) = \(\frac{4}{5}\) × 2
2 × \(\frac{4}{5}\) = \(\frac{2}{1}\) × \(\frac{4}{5}\) write 2 as a fraction
= \(\frac{2 \times 4}{1 \times 5}\) ← Multiply the numerators
← Multiply the denominators
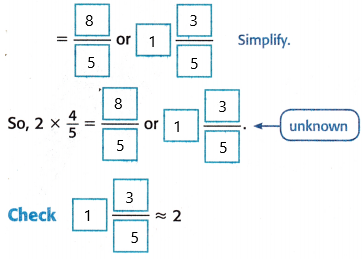
Answer:
The above-given equation:
2 x 4/5
Now we have to write 2 as a fraction.
2/1 x 4/5 =
Talk Math
Explain how you could find the product of 50 and \(\frac{2}{5}\) mentally.
Answer:
The above-given:
50 x 2/5
write 50 as a fraction
50/1 x 2/5
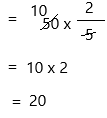

Guided Practice
Question 1.
Find \(\frac{1}{2}\) × 4. Write in simplest form.
\(\frac{1}{2}\) × 4 = \(\frac{1}{2}\) × \(\frac{4}{1}\) write 4 as \(\frac{4}{1}\)
= \(\frac{1 \times 4}{2 \times 1}\) Multiply
= ![]() or _____ simplify
or _____ simplify
So, \(\frac{1}{2}\) × 4 = ______.
Answer:
The above-given:
1/2 x 4
write 4 as a fraction.
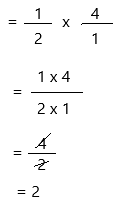
Therefore, \(\frac{1}{2}\) × 4 = 2.
Independent Practice
Multiply. Write in simplest form.
Question 2.
\(\frac{1}{3}\) × 12 = ____
Answer:
The above-given:
1/3 x 12
write 12 in fractions.
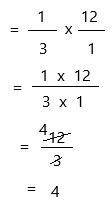
Therefore, \(\frac{1}{3}\) × 12 = 4.
Question 3.
\(\frac{1}{4}\) × 20 = ____
Answer:
The above-given equation:
1/4 x 20
write 20 as a fraction
= 1/4 x 20/1
= 1 x 20/ 4 x 1
= 20 / 4
= 5
Therefore, \(\frac{1}{4}\) × 20 = 5
Question 4.
\(\frac{5}{6}\) × 18 = ____
Answer:
The above-given equation:
5/6 x 18
write 18 as a fraction
= 5/6 x 18/1
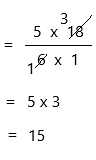
Therefore, \(\frac{5}{6}\) × 18 = 15
Question 5.
\(\frac{1}{5}\) × 7 = ____
Answer:
The above-given equation:
1/5 x 7
write 7 as a fraction
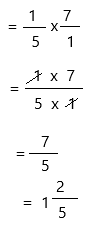
Therefore, \(\frac{1}{5}\) × 7 = 1 2/5.
Question 6.
\(\frac{2}{3}\) × 14 = ____
Answer:
The above-given equation:
2/3 x 14
write 14 as a fraction,
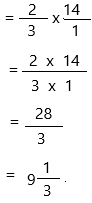
Therefore, \(\frac{2}{3}\) × 14 = 9 1/3.
Question 7.
\(\frac{2}{5}\) × 11 = ____
Answer:
The above-given equation:
2/5 x 11
write 11 as a fraction
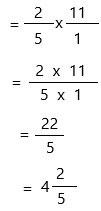
Therefore, \(\frac{2}{5}\) × 11 = 4 2/5
Question 8.
12 × \(\frac{1}{6}\) = ____
Answer:
The above-given equation:
12 x 1/6
write 12 as a fraction
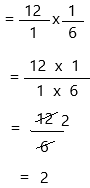
Therefore, 12 × \(\frac{1}{6}\) = 2
Question 9.
13 × \(\frac{2}{13}\) = ____
Answer:
The above-given equation:
13 x 2/13
write 13 as a fraction
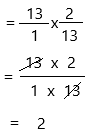
Therefore, 13 × \(\frac{2}{13}\) = 2
Question 10.
24 × \(\frac{3}{4}\) = ____
Answer:
The above-given equation:
24 x 3/4
write 24 as a fraction.
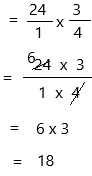
Therefore, 24 × \(\frac{3}{4}\) = 18
Mathematical Practice 2 Use Algebra Find the unknown in each equation. Write in simplest form.
Question 11.
5 × \(\frac{1}{4}\) = ![]()
![]() = ____
= ____
Answer:
The above-given equation:
5 x 1/4
write 5 as a fraction.
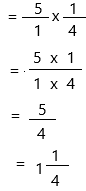
Therefore, 5 × \(\frac{1}{4}\) = 1 1/4.
Question 12.
15 × \(\frac{7}{10}\) = ![]()
![]() = ____
= ____
Answer:
The above-given:
15 x 7/10
write 15 as a fraction.
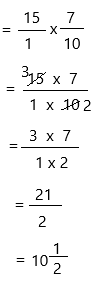
Therefore, 15 × \(\frac{7}{10}\) = 10 1/2
Question 13.
32 × \(\frac{5}{6}\) = ![]()
![]() = ____
= ____
Answer:
The above-given:
32 x 5/6
write 32 as a fraction.
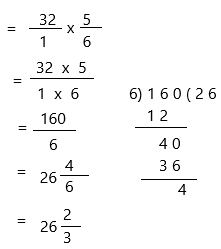
Therefore, 32 × \(\frac{5}{6}\) = 26 2/3
Problem Solving
Question 14.
Arleta is making nacho cheese dip for a party. She needs to make 5 batches. How much salsa will she need?

Answer:
The number of batches she needs to make = 5
The salsa she need = S
S = 5 x 1/2
S = 5/2
In mixed fraction, we can write 2 1/2
Therefore, she needs 2 1/2 cups of salsa.
Question 15.
Maria ate \(\frac{1}{4}\) of a pizza. If there were 20 slices of pizza, how many slices did Maria eat?
Answer:
The above-given:
The amount of pizza Maria ate = 1/4
The number of slices of pizza she has = 20
The number of slices she ate = P
P = 1/4 x 20
P = 5
Therefore, she ate 5 slices of pizza.
Question 16.
Mathematical PRACTICE 4 Model Math Write and solve a real-world problem that involves multiplying 8 × \(\frac{5}{8}\).
Answer:
Maria ate \(\frac{5}{8}\) of a pizza. If there were 8 slices of pizza, how many slices did Maria eat?
The equation is given:
8 x 5/8 = 5
8 and 8 get cancelled and the remaining number is 5
Therefore, she ate 5 slices of pizza.
HOT Problems
Question 17.
Mathematical PRACTICE 3 Which One Doesn’t Belong? Circle the expression that does not belong with the other three Explain.
\(\frac{1}{2}\) × 12 9 × \(\frac{2}{3}\) \(\frac{1}{4}\) × 20 \(\frac{1}{6}\) × 36
Answer:
The above-given equations:
1/2 x 12 = 6
2/3 x 9 = 6
1/4 x 20 = 5
1/6 x 36 = 6
\(\frac{1}{4}\) × 20 does not belong with the other three.
If I could change the 20 to 24 then the product would be 6.
Question 18.
? Building on the Essential Question Can all whole numbers be written as fractions? Explain.
Answer:
Yes, any whole number can be written as a fraction by placing the whole number over a denominator of 1.
Suppose we have a whole number 6 and we want to represent it as a fraction.
It needs to be of the form p/q.
So the numerator p will be 6 and the denominator q will be 1 to give 6/1.
Thus, we divide the whole number by 1 to represent it as a fraction.
McGraw Hill My Math Grade 5 Chapter 10 Lesson 4 My Homework Answer Key
Practice
Multiply. Write in the simplest form.
Question 1.
\(\frac{2}{3}\) × 12 = ____
Answer:
The above-given equation:
2/3 x 12
write 12 as a fraction
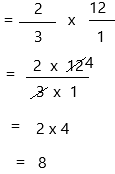
Therefore, \(\frac{2}{3}\) × 12 = 8
Question 2.
\(\frac{3}{10}\) × 8 = ____
Answer:
The above-given equation:
3/10 x 8
write 8 as a fraction
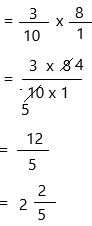
Therefore, \(\frac{3}{10}\) × 8 = 2 2/5.
Question 3.
8 × \(\frac{1}{5}\) = ____
Answer:
The above-given equation:
8 x 1/5
write 8 as a fraction.
= 8/1 x 1/5
= 8/5
In mixed fractions, we can write as 1 3/5.
Question 4.
13 × \(\frac{1}{2}\) = ____
Answer:
The above-given equation:
13 x 1/2
write 13 as a fraction
13/1 x 1/2
= 13/2
In mixed fractions, we can write 6 1/2.
Question 5.
20 × \(\frac{3}{5}\) = ____
Answer:
The above-given equation:
20 x 3/5
write 20 as a fraction
= 20/1 x 3/5
= 60/5
= 12
Therefore, 20 × \(\frac{3}{5}\) = 12
Question 6.
\(\frac{3}{10}\) × 7 = ____
Answer:
The above-given equation:
3/10 x 7
write 7 as a fraction
= 3/10 x 7/1
= 21/10
In mixed fractions, we can write as 2 1/10.
Problem Solving
Question 7.
The length of a popcorn machine is \(\frac{3}{4}\) of its height. What is the length of the machine?

Answer:
The above-given:
The length of popcorn = 3/4
The height of the machine = 24
The length of the machine = M
M = 24 x 3/4 [ 4 x 6 = 24]
M = 6 x 3
M = 18
Question 8.
Quinten is making bread and wants to triple the recipe. The recipe calls for \(\frac{2}{3}\) cup of sugar. How much sugar will he need?
Answer:
The above-given:
Quinten wants to triple the recipe means 3 times.
The equation can be written as:
2/3 x 3 = 2/3 + 2/3 + 2/3
If we solve the equation 2/3 x3
write 3 as a fraction.
2/3 x 3/1
= 2 x 3/ 3 x 1
= 6/3
= 2.
Therefore, he needs e cups of sugar.
Question 9.
Joaquin has $24. He used \(\frac{5}{8}\) of his money to buy a pair of jeans. How much money did Joaquin spend on jeans?
Answer:
The above-given:
The amount Joaquin has = 24
The amount of money he used = 5/8
The money he spends on jeans = J
J = 24 x 5/8 [ 8 x 3 = 24]
J = 3 x 5
J = 15
Therefore, he spends $15 on jeans.
Question 10.
Mathematical PRACTICE 2 Use Number Sense Write and solve a real-world problem involving the multiplication of a fraction and a whole number whose product is between 10 and 15.
Answer:
Jean is working in a pizza shop. She has 60 kg of flour. She has used one-sixth of it for making pizzas. How much flour does she need?
60 x 1/6 = 10
therefore, the product is 10.
If we replace 1/6 with 1/4
– Jean is working in a pizza shop. She has 60 kg of flour. She has used one-fourth of it for making pizzas. How much flour does she need?
60 x 1/4 = 15
Therefore, the product is 15.
Test Practice
Question 11.
Rico is making punch for 18 people. How much punch should Rico make if each person will drink \(\frac{1}{6}\) gallon of punch?
A. 2 gallons
B. 3 gallons
C. 4 gallons
D. 5 gallons
Answer: Option B is correct.
The above-given:
The number of people = 18
The gallon of punch = 1/6
The number of punch = P
P = 1/6 x 18
P = 3
Therefore, he can make 3 punches.