All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 3 Model Fraction Multiplication will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 3 Model Fraction Multiplication
Draw It
Find \(\frac{1}{3}\) × 3. Use repeated addition.
1. Since the denominator is 3, each model is divided into ___ equal sections.
Answer:
The above-given;
1/3 x 3
We need to divide three sections as the denominator is 3.
2. Shade \(\frac{1}{3}\) of each model.
How many sections of each model are shaded? ____
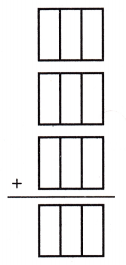
Add. How many total sections of the models are shaded? ____ ← Shade this number of sections on the last model.
Answer:
We need to shade each model.
The diagram can be represented as:
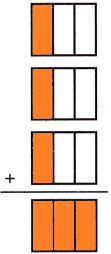
In each model, we shaded one.
Finally, 3 sections were shaded.
3. The last model shows the product of \(\frac{1}{3}\) × 3.

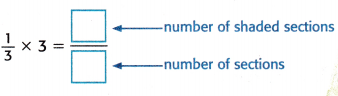
What is \(\frac{3}{3}\) equal to?
So, \(\frac{1}{3}\) × 3 = 3 ÷ 3, or ____
Answer:
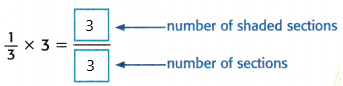
Thus, 3/3 = 1
Therefore, \(\frac{1}{3}\) × 3 = 3 ÷ 3, or 1.
Try It
Find the unknown in 2 × \(\frac{3}{4}\) = ![]() . Use models. Write in simplest form.
. Use models. Write in simplest form.
1. Divide each model below into ____ equal sections since the denominator is 4.
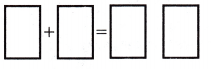
Answer:
as the denominator is 4 we divide the sections into 4 parts.
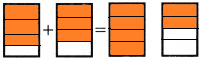
2. Shade \(\frac{3}{4}\)– of each of the first two models.
How many sections of each model are shaded? _____
Add. How many total sections of the models are shaded? ____ ← Shade this number of sections on the last two models.
Answer:
The above-given fraction: 3/4
3 sections are shaded in each model.
The total sections are 6.
3. The last two models show the product of 2 × \(\frac{3}{4}\).

What is \(\frac{6}{4}\) equal to? 
So, 2 × \(\frac{3}{4}\) =  ← unknown
← unknown
Answer:
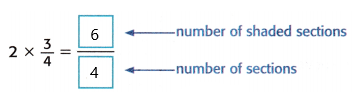
6/4 = 3/2
In mixed fractions, we can write as 1 1/2.
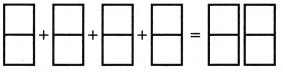
Therefore, 2 × \(\frac{3}{4}\) = 
Helpful Hint
2 × \(\frac{3}{4}\) is the same as 3 × 2 ÷ 4.
Talk About It
Question 1.
Explain why 2 × \(\frac{3}{4}\) is the same as 3 × 2 ÷ 4.
Answer:
Because if we calculate both equations we get the same fraction.
2 x 3/4 = 6/4 = 3/2
3 × 2 ÷ 4
= 6/4 = 3/2
2 x 3/4 = 3 × 2 ÷ 4
3/2 = 3/2
Therefore, LHS = RHS
Question 2.
Mathematical PRACTICE 2 Reason Explain how you could find 2 × \(\frac{3}{4}\) without using models.
Answer:
By calculating the equation we can solve the fraction without using the model.
– Generally, the fraction can be a portion of any quantity out of the whole thing and the whole can be any specific thing or value. The basics of fractions explain the top and bottom numbers of a fraction. The top number represents the number of selected or shaded parts of a whole whereas the bottom number represents the total number of parts.
– Suppose a number has to be divided into four parts, then it is represented as x/4. So the fraction here, x/4, defines 1/4th of the number x. Hence, 1/4 is the fraction here. It means one in four equal parts. It can be read as one-fourth or 1/4. This is known as a fraction.
2 x 3/4 = 6/4 = 3/2 = 1 1/2.
Practice It
Shade the models to find each product. Write in the simplest form.
Question 3.
4 × \(\frac{1}{2}\) = _____
Answer:
The above-given:
4 x 1/2
as the value of the denominator is 2.
so we have to divide the sections into 2 equal parts.
if we calculate the fraction, then we get 2.
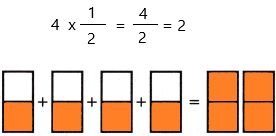
Question 4.
4 × \(\frac{1}{3}\) = _____
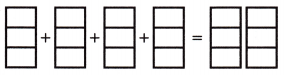
Answer:
The above-given:
4 x 1/3
as the denominator is 3 so we divide the sections into 3 equal parts.
if we calculate the fraction, then we get 4/3 and in mixed fractions, we get 1 1/3.
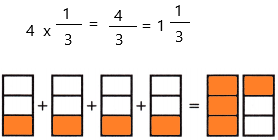
Question 5.
\(\frac{2}{3}\) × 5 = _____
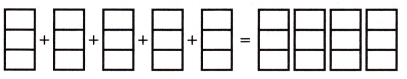
Answer:
The above-given:
2/3 x 5
as the value of the denominator is 3 so we divide the sections into 3 equal parts.
if we calculate the fraction then we get 10/3. In mixed fractions, we can write 3 1/3.
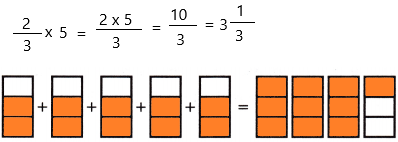
Question 6.
3 × \(\frac{2}{3}\) = _____
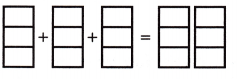
Answer:
The above-given:
3 x 2/3
as the value of the denominator is 3 so we divided the sections into 3 equal parts.
If we calculate the fraction then we get 6/3 which is 2.
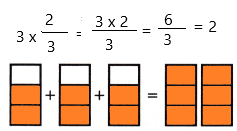
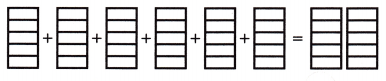
Algebra Find each unknown. Shade the models to find each product. Write in simplest form.
Question 7.
\(\frac{1}{5}\) × 6 = ![]()
![]() = ____
= ____
Answer:
The above-given:
1/5 x 6
as the value of the denominator is 5 so we divided the sections into 5 equal parts.
if we calculate the fraction then we get 6/5. In mixed fractions, we can write as 1 1/5
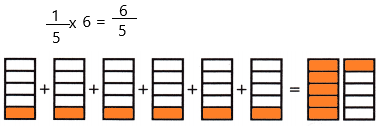
Question 8.
\(\frac{2}{5}\) × 6 = ![]()
![]() = ____
= ____

Answer:
The above-given:
2/5 x 6
as the value of the denominator is 5 so we divided the sections into 5 equal parts.
if we calculate the fraction then we get 12/5. In mixed fractions, we can write 2 2/5.
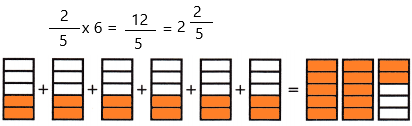
Apply It
Algebra Use models to help you solve Exercises 9 and 10. Then complete the equation.
Question 9.
Brandon saved 2 gigabytes of music on his MP3 player. Of the music saved, \(\frac{1}{4}\) is hip hop. What fraction of a gigabyte did Brandon use for his hip hop music?
Equation: 2 × \(\frac{1}{4}\) = 2 ÷ ____, or ![]()
Answer:
The above-given:
2 x 1/4 = 2 ÷ 4
as the value of the denominator is 4 then we divide the section into 4 equal parts.
if we solve the equation,
2 x 1/4 = 2/4 = 1/2.
Therefore, the fraction of a gigabyte did Brandon use for his hip hop music is 1/2.
Question 10.
Mathematical Practice 4 Model Math Over the past 6 hours, Natalie spent \(\frac{1}{5}\) of each hour kneading bread. How much time did she spend kneading bread in all?
Equation: 6 × \(\frac{1}{5}\) = 6 ÷ ___, or ![]()

Answer:
The above-given equation:
6 x 1/5 = 6 ÷ 5 = 6/5 = 1 1/5.
If we solve the equation then we get 6/5
therefore, the time she spends is 1 1/5 of the hour kneading bread.

Question 11.
Mathematical PRACTICE 1 Plan Your Solution Write and solve a real-world problem that could be represented by the model below.
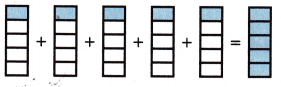
Answer:
The real-world problem would be Over the past 5 hours, Natalie spent \(\frac{1}{5}\) of each hour kneading bread. How much time did she spend kneading bread in all?
The equation would be:
5 x \(\frac{1}{5}\) = 5 ÷ 5
If we solve the equation:
5 x 1/5 = 5/5 = 1.
Therefore, she spends 1-hour kneading bread in all.
Write About It
Question 12.
Explain why \(\frac{2}{3}\) × 12 can be written as 2 × 12 ÷ 3.
Answer:
because both are equal but their representation is different.
2/3 x 12 = 24/3 = 8
2 × 12 ÷ 3
In this equation, first, we have to multiply and then divide.
There are certain rules for algebraic symbols to calculate.
In this case, we need to multiply first.
24 ÷ 3 = 8.
Therefore, both are equal.
McGraw Hill My Math Grade 5 Chapter 10 Lesson 3 My Homework Answer Key
Practice
Shade the models to find each product. Write in simplest form.
Question 1.
4 × \(\frac{2}{3}\) = _____
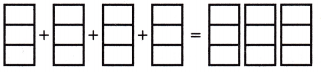
Answer:
The above-given:
4 x 2/3
as the value of the denominator is 3 so we divided the sections into 3 equal parts.
If we solve the equation then we get 8/3. In mixed fractions, we can write 2 2/3.
4 x 2/3 = 8/3 = 2 2/3.
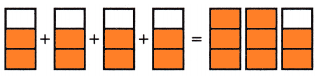
Question 2.
\(\frac{3}{4}\) × 2 = _____
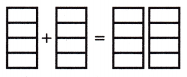
Answer:
The above-given:
3/4 x 2
as the value of the denominator is 4 so we divided the sections into 4 equal parts.
If we solve the equation then we get 6/4. In mixed fractions, we can write 1 1/2
3/4 x 2 = 6/4 = 3/2 = 1 1/2.
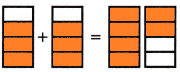
Problem Solving
Mathematical PRACTICE 4 Model Math Use models to help you solve Exercises 3-5. Then complete the equation.
Question 3.
Melinda spent 4 hours reviewing for her midterm exams. She spent \(\frac{1}{4}\) of the time studying for social studies. How many hours did she spend on social studies?
________________________________
Equation: 4 × \(\frac{1}{4}\) = 4 ÷ ____, or ![]()
Answer:
The above-given equation:
4 x 1/4 = 4 ÷ 4 = 1
If we calculate the fraction then we get the answer 1.
Therefore, she spends 1 hour on social studies.
The model can be represented as:
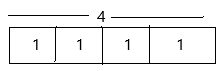
Question 4.
Cody wants to watch a new movie that is 3 hours long. He has watched \(\frac{1}{6}\) of the movie so far. What fraction of one hour did Cody spend watching the new movie?
Equation: 3 × \(\frac{1}{6}\) = 3 ÷ ____, or ![]()
Answer:
The above-given equation:
3 x 1/6 = 3 ÷ 6 = 1/2
Therefore, Cody spends 1/2 hour watching the new movie.
Question 5.
The distance from Paula’s house to school is 5 miles. There is a set of railroad tracks one-fourth of the distance away from her house. How many miles away are the railroad tracks from Paula’s house?
Equation: 5 × \(\frac{1}{4}\) = 5 ÷ ____, or ![]()

Answer:
The above-given equation:
5 x 1/4 = 5 ÷ 4 = 5/4
In mixed fractions, we can write as 1 1/4
Therefore, 1 1/4 miles away are the railroad tracks from Paula’s house.