All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 2 Estimate Products of Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 2 Estimate Products of Fractions
Math in My World
Example 1
About \(\frac{1}{3}\) of the containers of yogurt in a box are strawberry. If the box contains 17 containers. about how many containers are strawberry?

Estimate \(\frac{1}{3}\) × 17.
Use compatible numbers.
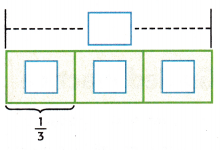
\(\frac{1}{3}\) × 17 ≈ \(\frac{1}{3}\) × ____ ← What number is close to 17 and also compatible with 3?
Complete the bar diagram to find the product of \(\frac{1}{3}\) × ____.
How many yoghurt containers are represented in each section of the bar diagram? ____
So, \(\frac{1}{3}\) × 18 = ____
About ____ yoghurt containers are strawberry.
Answer:
The above-given:
1/3 x 17
The number is close to 17 and compatible with 3.
The number is 18.
1/3 x 18 = 6
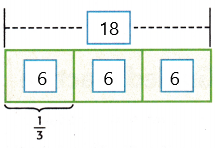
Therefore, 6 yoghurt containers are strawberry.
Helpful Hint
\(\frac{1}{3}\) × 18 is the same as 18 ÷ 3.
Example 2
Estimate \(\frac{2}{5}\) × \(\frac{6}{7}\).
Use a number line to round each fraction to 0, \(\frac{1}{2}\) or 1.
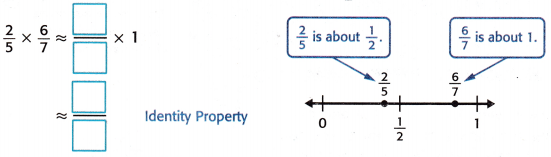
So, \(\frac{2}{5}\) × \(\frac{6}{7}\) is about ![]()
Answer:
The above-given:
2/5 is about 1.
6/7 is about to 1.
Now substituted the values.
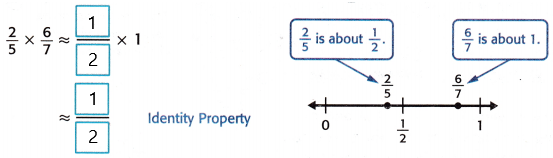
Therefore, 2/5 x 6/7 is about 1/2.
Example 3
Estimate 7\(\frac{2}{7}\) × 3\(\frac{7}{8}\).
Round each mixed number to the nearest whole number.
Round 7\(\frac{2}{7}\) down to ____ and round 3\(\frac{7}{8}\) up to ____
7\(\frac{2}{7}\) × 3\(\frac{7}{8}\) ≈ ____ × ____
≈ ____
So, 7\(\frac{2}{7}\) × 3\(\frac{7}{8}\) is about ____
Answer:
The above-given:
7 2/7 x 3 7/8
The given fractions are mixed fractions.
7 2/7 = 7 x 7/7 + 2/7 = 49/7 + 2/7 = 51/7 = 7.28 (the closest number is 7)
3 7/8 = 8 x 3/8 + 7/8 = 24/8 + 7/8 = 31/8 = 3.875 (the closest number is 4)
So, we can write,
7 2/7 + 3 7/8 = 7 x 4 = 28
Therefore, 7\(\frac{2}{7}\) × 3\(\frac{7}{8}\) is about 28.
Talk Math
Explain how you would estimate the product of \(\frac{4}{5}\) × \(\frac{5}{6}\).
Answer:
The above-given product:
4/5 x 5/6
The estimated value of 4/5 is 1
The estimated value of 5/6 is 1
Multiply the products.
The product = 1 x 1 = 1.
Therefore, the estimated product of \(\frac{4}{5}\) × \(\frac{5}{6}\) is 1.

Guided Practice
Question 1.
Estimate the product of \(\frac{1}{2}\) × 25. Use compatible numbers.
\(\frac{1}{2}\) × 25 ≈ \(\frac{1}{2}\) × ____ Think: What is half of 24?
So, \(\frac{1}{2}\) × 25 is about ____
Answer:
The above-given:
1/2 x 25 ≈ 1/2 x 24
Now calculate for 1/2 of 24
1/2 x 24 = 12
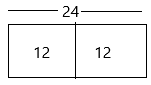
Therefore, \(\frac{1}{2}\) × 25 is about 12.
Independent Practice
Estimate each product. Draw a bar diagram if necessary.
Question 2.
\(\frac{1}{2}\) × 13
Answer:
The above-given
1/2 x 13
The estimated value would be 12
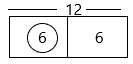
1/2 x 12 = 6
Therefore, the answer is 6.
Question 3.
\(\frac{1}{3}\) × 20
Answer:
The above-given:
1/3 x 20
Now round up the product 20 to 21.
Now the product is
1/3 x 21 = 7
Now draw the bar diagram:
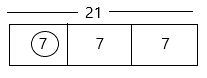
Therefore, the answer is 7.
Question 4.
\(\frac{1}{2}\) × 33
Answer:
The above-given:
1/2 x 33
Now we can round down the value from 33 to 32.
The estimated product:
1/2 x 32 = 16
The bar diagram is represented as:
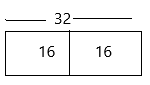
Therefore, the answer is 16.
Question 5.
17 × \(\frac{1}{4}\)
Answer:
The above-given:
17 x 1/4
Now we can round down the product from 17 to 16.
16 x 1/4 = 4
Now the bar diagram is represented as:
we have to divide the four sections as the denominator is having 4.
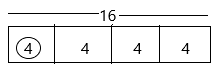
Therefore, the answer is 4.
Question 6.
\(\frac{7}{8}\) × \(\frac{1}{9}\)
Answer:
The above-given:
The estimated value of 7/8 = 0.875 (the closest value is 1)
The estimated value of 1/9 = 0.11 (the closest value is 0)
Now multiply both the estimated products.
The product = 1 x 0 = 0
Therefore, the answer is 0.
Question 7.
\(\frac{3}{5}\) × \(\frac{8}{9}\)
Answer:
The above-given:
3/5 x 8/9
Now we have to find out the estimated products.
The estimated value of 3/5:
3/5 ≈ 2/4 = 1/2
The estimated value of 8/9 = 1
Now multiply both the products.
The product = 1/2 x 1 = 1/2.
Question 6.
\(\frac{1}{6}\) × \(\frac{5}{7}\)
Answer:
The above-given:
1/6 x 5/7
Now we have to find out the estimated products.
The estimated value of 1/6 is 0.
The estimated value of 5/7 is 1
Now multiply the products.
The product: 1 x 0 = 0
Therefore, the estimated product of \(\frac{1}{6}\) × \(\frac{5}{7}\) is 0.
Question 7.
\(\frac{1}{4}\) × \(\frac{8}{9}\)
Answer:
The above-given:
1/4 x 8/9
Now we have to find out the estimated products.
The estimated value of 1/4 is 0
The estimated value of 8/9 is 1
Now multiply both the products
The product = 0 x 1 = 0
Therefore, the estimated product of \(\frac{1}{4}\) × \(\frac{8}{9}\) is 0.
Question 8.
\(\frac{1}{6}\) × \(\frac{5}{7}\)
Answer:
The above-given:
1/6 x 5/7
Now we have to find out the estimated products.
The estimated value of 1/6 is 0.
The estimated value of 5/7 is 1
Now multiply the products.
The product: 1 x 0 = 0
Therefore, the estimated product of \(\frac{1}{6}\) × \(\frac{5}{7}\) is 0.
Question 9.
\(\frac{1}{4}\) × \(\frac{8}{9}\)
Answer:
The above-given:
1/4 x 8/9
Now we have to find out the estimated products.
The estimated value of 1/4 is 0
The estimated value of 8/9 is 1
Now multiply both the products
The product = 0 x 1 = 0
Therefore, the estimated product of \(\frac{1}{4}\) × \(\frac{8}{9}\) is 0.
Question 10.
2\(\frac{2}{3}\) × 3\(\frac{1}{6}\)
Answer:
The above-given:
2 2/3 x 3 1/6
They are in mixed fractions, now convert them into proper fractions.
2 2/3 = 3 x 2/3 + 2/3 = 6/3 + 2/3 = 8/3.
3 1/6 = 6 x 3/6 + 1/6 = 18/6 + 1/6 = 19/6
The estimated value of 8/3 is 3
The estimated value of 19/6 is 3
Now multiply both the estimated values.
The product = 3 x 3 = 9
Therefore, the estimated product of 2\(\frac{2}{3}\) × 3\(\frac{1}{6}\) is about 9.
Question 11.
6\(\frac{4}{5}\) × 5\(\frac{7}{8}\)
Answer:
The above-given:
6 4/5 x 5 7/8
They are in mixed fractions, now convert them into proper fractions.
6 4/5 = 5 x 6/5 + 4/5 = 30/5 + 4/5 = 34/5
5 7/8 = 8 x 5/8 + 7/8 = 40/8 + 7/8 = 47/8
Now we have to find out the estimated products.
The estimated value of 34/5:
34/5 ≈ 35/5 = 7
The estimated value of 47/8
47/8 ≈ 48/8 = 6
Now multiply both the products.
The product = 7 x 6 = 42.
Therefore, the estimated product of 6\(\frac{4}{5}\) × 5\(\frac{7}{8}\) is about 42.
Question 12.
10\(\frac{1}{7}\) × 4\(\frac{4}{5}\)
Answer:
The above-given:
10 1/7 x 4 4/5
They are in mixed fractions, now convert them into proper fractions.
10 1/7 = 7 x 10/7 + 1/7 = 70/7 + 1/7 = 71/7
4 4/5 = 5 x 4/5 + 4/5 = 20/5 + 4/5 = 24/5
Now we have to find out the estimated products.
The estimated value of 71/7
71/7 ≈ 70/7 = 10
The estimated value of 24/5
24/5 ≈ 25/5 = 5
Now multiply both the products.
The product = 10 x 5 = 50
Therefore, the estimated product of 10\(\frac{1}{7}\) × 4\(\frac{4}{5}\) is about 50.
Question 13.
2\(\frac{6}{7}\) × 6\(\frac{2}{9}\)
Answer:
The above-given:
2 6/7 x 6 2/9
They are in mixed fractions, now convert them into proper fractions.
2 6/7 = 7 x 2/7 + 6/7 = 14/7 + 6/7 = 20/7
6 2/9 = 9 x 6/9 + 2/9 = 54/9 + 2/9 = 56/9
Now we have to find out the estimated products.
The estimated value of 20/7
20/7 ≈ 18/6 = 3
The estimated value of 56/9
56/9 ≈ 60/10 = 6
Now multiply both the products.
The product = 3 x 6 = 18
Therefore, the estimated product of 2\(\frac{6}{7}\) × 6\(\frac{2}{9}\) is about 18.
Problem Solving
Question 14.
A cup of chocolate chips weighs about 9 ounces. A recipe calls for 3\(\frac{3}{4}\) cups of chocolate chips. About how many ounces of chocolate chips are needed?
Answer:
The above-given:
The weight of a cup of chocolate chips = 9
The number of cups of chocolate chips a recipe calls = 3 3/4 = 15/4
The estimated value for 15/4:
15/4 ≈ 16/4 = 4.
Now we need to find out the number of ounces of chocolate chips needed. Let it be C.
C = 9 x 4
C = 36.
Therefore, 36 ounces of chocolate chips are needed.
Question 15.
Mathematical PRACTICE 5 Use Math Tools Isabella sent out 22 invitations to her birthday party. If about \(\frac{1}{4}\) of the invitations are for her school friends, how many invitations are for her school friends? Draw a bar diagram to help you solve.

Answer:
The above-given:
The number of invitationsIsabella sent to her birthday party = 22
The number of invitations for school friends = 1/4 (in fractions given)
Now we need to find out in number.
The number of invitations = S
S = 22 x 1/4
Now we can estimate the value of 22.
The estimated value of 22 is 24.
S = 24 x 1/4
S = 6
The bar diagram can be represented as:
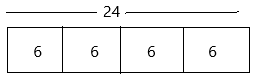
Therefore, she sent 6 invitations for her school friends.
HOT Problems
Question 16.
Mathematical PRACTICE 1 Make a Plan Write a real-world problem involving the multiplication of two mixed numbers whose product is about 14. Then solve the problem.
Answer:
Chelsie has 2 1/2 containers to put her special designer fabric that is 6 1/2 inches long. Chelsie currently has 2 copies. how many inches long is both fabric?
Solving the equation:
The equation: 2 1/2 x 6 1/2 = 14
2 1/2: it is in a mixed fraction, now convert it into a proper fraction.
2 1/2 = 2 x 2/2 + 1/2 = 4/2 + 1/2 = 5/2
6 1/2 = 2 x 6/2 + 1/2 = 12/2 + 1/2 = 13/2.
The estimated value of 5/2:
5/2 ≈ 4/2 = 2
The estimated value of 13/2
13/2 ≈ 14/2 = 7
Now multiply both the products.
The product = 2 x 7 = 14
Therefore, the answer is proved.
Question 17.
? Building on the Essential Question Explain when estimation would not be the best method for solving a problem.
Answer:
Even the most seasoned project management professionals can draft estimates that miss the mark. When they occur they’re usually off by just a little, though occasionally they’re off by miles. But because so much of the project management process relies on these estimates, even a minor flaw can have a large impact on the team’s ability to achieve success.
– Finally, in projects, we cannot use estimations that lead to calculation errors and miscommunications about the information received from the external partner.
McGraw Hill My Math Grade 5 Chapter 10 Lesson 2 My Homework Answer Key
Practice
Estimate each product. Draw a bar diagram if necessary.
Question 1.
\(\frac{2}{3}\) × 26
Answer:
The above-given:
2/3 x 26
We can estimate 26 as 27.
2/3 x 27 = 2 x 9 = 18
The bar diagram can be represented as:
– we need to divide 3 sections as the value of the denominator is 3.
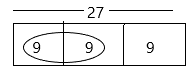
The fraction is 2/3 so we rounded two 9’s.
The answer is 18.
Therefore, the estimated product of \(\frac{2}{3}\) × 26 is about 18.
Question 2.
\(\frac{7}{8}\) × \(\frac{5}{6}\)
Answer:
The above-given:
7/8 x 5/6
The estimated value of 7/8 is 1
The estimated value of 5/6 is 1
Now multiply both the estimated products.
The product = 1 x 1 = 1
Therefore, the estimated product of \(\frac{7}{8}\) × \(\frac{5}{6}\) is about 1.
Question 3.
5\(\frac{1}{5}\) × 8\(\frac{5}{6}\)
Answer:
The above-given:
5 1/5 x 8 5/6
They are in mixed fractions, now convert them into proper fractions.
5 1/5 = 5 x 5/5 +1/5 = 25/5 + 1/5 = 26/5
8 5/6 = 6 x 8/6 + 5/6 = 48/6 + 5/6 = 53/6
Now we have to find out the estimated product.
The estimated value of 26/5:
26/5 ≈ 25/5 = 5
The estimated value of 53/6:
53/6 ≈ 54/6 = 9
Now multiply both the estimated products
The product = 5 x 9 = 45
Therefore, the estimated product of 5\(\frac{1}{5}\) × 8\(\frac{5}{6}\) is about 45.
Problem Solving
Use the table to answer Exercises 4 and 5.
Question 4.
Mathematical PRACTICE 3 Justify Conclusions The table shows the results of a class survey about pets. Suppose 53 students were surveyed. About how many students have one pet? Justify your answer.
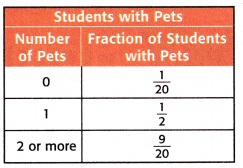
Answer:
The number of students was surveyed = 53
The number of students has one pet = P
P = 1/2 x 53
We can estimate the number 53 as 50.
P = 1/2 x 50
P = 25
Therefore, 25 students have one pet.
Question 5.
If 100 students are surveyed, about how many students own 2 or more pets? Explain.
Answer:
The number of students surveyed = 100
The number of students who own 2 or more pets = P1
P1 = 9/20 x 100
P1 = 9 x 5
P1 = 45
Therefore, 45 student owns 2 or more pets.
Question 6.
A rectangular floor measures 10\(\frac{1}{8}\) feet by 13\(\frac{3}{4}\) feet. If Mary buys 150 square feet of carpet, will she have enough carpet to cover the floor?
Answer:
The number of square feet of carpet Mary buys = 150
The given measurements of the floor:
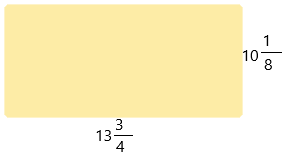
The given mixed fractions are:
10 1/8 and 13 3/4
Convert them into proper fractions.
10 1/8 = 81/8; 13 3/4 = 55/4
The estimated value of 81/8:
81/8 ≈ 80/8 = 10
The estimated value of 55/4
55/4 ≈ 52/4 = 13
Now multiply both the products:
The product = 10 x 13 = 130.
Yes, she has enough carpet to cover the floor.
Test Practice
Question 7.
A cup of water holds about 8 ounces. If a recipe calls for \(\frac{1}{3}\) cup of water, which is the best estimate of the number of ounces that are needed? Draw a bar diagram if necessary.
A. 1 ounce
B. 3 ounces
C. 6 ounces
D. 8 ounces
Answer: Option B is correct.
Explanation:
The above-given:
The number of ounces of water a cup can hold = 8
The cup of water a recipe calls = 1/3
The best estimation. Let it be O.
O = 8 x 1/3
We can estimate 8 as 9.
O = 9 x 1/3
O = 3
Therefore, 3 ounces are needed.
The bar diagram can be represented as: