All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 1 Lesson 4 Represent Decimals will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 1 Lesson 4 Represent Decimals
Math in My World
Example 1
A bee hummingbird weighs only about \(\frac{56}{1,000}\) of an ounce. Represent this fraction as a decimal. Then write it in word form.

Question 1.
The model represents thousandths by showing one thousand small cubes.
Shade ____ of the small cubes.
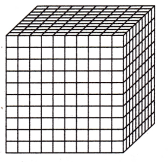
Answer:
The above-given model represents the thousandths
We need to shade 56 small cubes
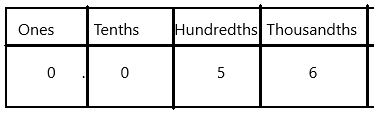
Question 2.
The fraction names thousandths, so there should be three digits to the right of the decimal point.
\(\frac{56}{1,000}\) = 0 ![]()
Answer:
In fractions, we can write as 56/1000
In decimals, we can write as 0.056
Question 3.
Write \(\frac{56}{1,000}\) in word form. 
So, \(\frac{56}{1,000}\) is __________
Answer:
In word form, we can write as fifty-six thousandths
Example 2
Model \(\frac{35}{100}\). Then write it ¡n word form and as a decimal.
Question 1.
Shade ___ of the small squares.

Answer:
In fractions, we can write as 35/100
we have to shade 35 small squares

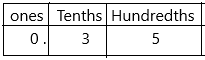
Question 2.
The fraction names thirty-five ____, so there should be two digits to the right of the decimal point.
So, \(\frac{35}{100}\) is thirty-five hundredths and 0. ![]()
Answer:
The fraction names are thirty-five hundredths.
In decimals, we can write them as 0.35
Guided Practice
Shade the model. Then write each fraction as a decimal.
Question 1.
\(\frac{2}{10}\)

Decimal: ____
Answer:
The above-given model is tenth cube
The given fraction is 2/10
In decimals, we can write it as 0.2

Talk Math
Describe a rule for writing fractions like \(\frac{8}{100}\) and \(\frac{32}{1,000}\) as decimals.

Answer:
Well, they are pretty much the same thing. They are both composed of one or more numerators and denominators.
– Fraction is divided into two parts, one is the numerator and the other is a denominator. According to the structure of the fraction, \frac command has been created in Latex, where you can pass two arguments.
\frac{numerator}{denominator}
– Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
The above-given fractions are 8/100; 32/1000
In decimals, we can write as 0.08 and 0.032
Question 2.
\(\frac{58}{100}\)

Decimal: ____
Answer:
The given model is hunderdths cube.
The above-given fraction 58/100
In decimals, we can write it as 0.58

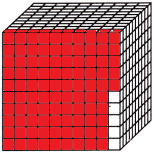
Question 3.
\(\frac{95}{1,000}\)

Decimal: ____
Answer:
The above-given model is the cube of the thousandth.
The above-given fraction 95/1000
In decimals, we can write it as0.095
Independent Practice
Shade the model. Then write each fraction ¡n word form and as a decimal.
Question 4.
\(\frac{3}{10}\)

Word form: ______
Decimal: ____
Answer:
The above-given model is the tenth cube
In decimal form, we can write it as0.3
In word form, we can write it as three-tenths.

Question 5.
\(\frac{86}{100}\)

Word form: ______
Decimal: ____
Answer:
The given model is a hundredths cube
The fraction is 86/100
In word form, we can write it as eighty-six hundredths.
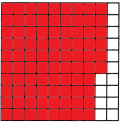
Question 6.
\(\frac{99}{100}\)

Word form: ______
Decimal: ____
Answer:
The given model is a hundredths cube
The fraction is 99/100
In word form, we can write it as ninety-nine hundredths.
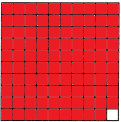
Question 7.
\(\frac{51}{1,000}\)
Word form: ______
Decimal: ____
Answer:
The above-given model is the cube of the thousandth.
The above-given fraction 51/1000
In decimals, we can write it as 0.051
In word form, we can write it as fifty-one thousandths.
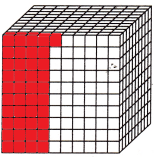
Question 8.
\(\frac{22}{1,000}\)

Word form: ______
Decimal: ____
Answer:
The above-given model is the cube of the thousandth.
The above-given fraction 22/1000
In decimals, we can write it as 0.022
In word form, we can write it as twenty-two thousandths.
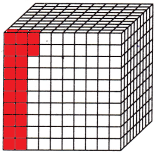
Question 9.
\(\frac{1}{1,000}\)

Word form: ______
Decimal: ____
Answer:
The above-given model is the cube of the thousandth.
The above-given fraction of 1/1000
In decimals, we can write it as 0.001
In word form, we can write it as one-thousandth.

Problem Solving
Question 10.
A runner decreased his time by \(\frac{5}{100}\) second. Express the decrease as a decimal.

Answer:
The above-given fraction of 5/100
In decimals, we can write them as 0.05

In word form, we can write as five hundredths.
Question 11.
Mathematical PRACTICE 2 Use Number Sense About \(\frac{7}{10}\) of a person’s body weight is water. Write this fraction in word form and as a decimal.
Answer:
The above-given fraction is 7/10
We need to write the given fraction in word form and decimal form.
In word form, we can write it as seven-tenths.
In decimal form, we can write it as 0.7
Write the customary measure for each metric measure as a decimal.
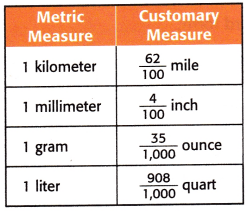
Question 12.
1 kilometer = _______
Answer:
In the above-given box,
1 km = 62/100
In decimals, we can write as 0.62
Question 13.
1 millimeter = _____
Answer:
In the above-given box,
1 mm = 4/100
In decimals, we can write them as 0.04
Question 14.
1 gram = ____
Answer:
In the above-given box,
1 gram = 35/1000
In decimals, we can write it as 0.035
Question 15.
1 liter = ______
Answer:
In the above-given box,
1 litre= 908/1000
In decimals, we can write them as 0.908
Hot Problems
Question 16.
Mathematical PRACTICE 3 Find the Error Dylan is writing \(\frac{95}{1,000}\) as a decimal. Find his mistake and correct it.
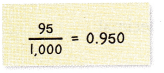
Answer:
The above-given fraction is 95/1000
There are certain rules:
Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
According to the above steps.
95/1000 in decimal is 0.095
Question 17.
? Building on the Essential Question How can the word form of a fraction help you write the fraction as a decimal?
Answer:
– A Fraction or a Mixed Number in which the Denominator is a power of 10 such as 10, 100, 1000. etc. usually expressed by the use of the Decimal point is termed as Decimal Fraction Math.
– In general, the word form of a fraction tells you what you can divide to generate the equivalent fraction. For instance, three-fourths can be converted to a decimal by completing the problem “three divided by four.”
– If the denominator is a multiple of ten, the word form of a fraction can tell you how many places are to the right of a decimal, as in case 47/100 = “forty-seven hundredths” = 0.47. Since the denominator is hundredths, you know that the decimal has two places to its right.
McGraw Hill My Math Grade 5 Chapter 1 Lesson 4 My Homework Answer Key
Practice
Shade the model. Then write each fraction in word form and as a decimal.
Question 1.
\(\frac{7}{10}\)

Answer:
The above-given model is the tenth cube.
The given fraction is 7/10
In decimal, we can write it as 0.7
In word form, we can write as seven-tenths.

Question 2.
\(\frac{62}{100}\)

Answer:
The above-given model is the hundredth cube.
The given fraction is 62/100
In word form, we can write as sixty-two hundredths
In decimal form, we can write it as 0.62

Question 3.
\(\frac{91}{1,000}\)
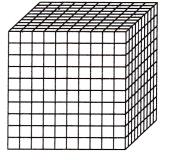
Answer:
The given model is the cube of thousandths
The above-given fraction 91/1000
In decimals, we can write it as 0.091
In word form, we can write as ninety-one thousandths.
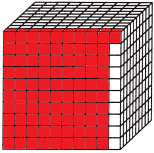
Question 4.
\(\frac{75}{1,000}\)
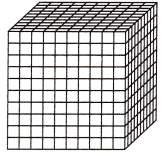
Answer:
The given model is the cube of thousandths
The above-given fraction 75/1000
In decimals, we can write it as 0.075
In word form, we can write as seventy-five thousandths.
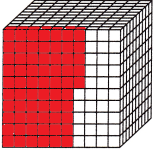
Write each fraction as a decimal.
Question 5.
\(\frac{15}{100}\) = ______
Answer:
The given fraction is 15/100
Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
In decimals, we can write as 0.15
Question 6.
\(\frac{129}{1,000}\) = ______
Answer:
The above-given fraction is 129/1000
Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
In decimals, we can write it as 0.129
Question 7.
\(\frac{17}{100}\) = ______
Answer:
The above-given fraction is 17/100
Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
In decimals, we can write it as 0.17
Question 8.
\(\frac{8}{10}\) = ______
Answer:
Th given fraction is 8/10
Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
In decimals, we can write as 0.8
Question 9.
\(\frac{815}{1,000}\) = ______
Answer:
The above-given fraction is 815/1000
Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
In decimals, we can write it as 0.815
Question 10.
\(\frac{2}{10}\) = ______
Answer:
The above-given fraction 2/10
Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
In decimals, we can write it as 0.2
Problem Solving
Question 11.
Mathematical PRACTICE 2 Reason Trudy is making a picture frame and needs nails that measure 0.375 inch. At the hardware store, nails are measured in fractions of an inch: \(\frac{125}{1,000}\) inch, \(\frac{25}{100}\) inch, and \(\frac{375}{1,000}\) inch. Which of these nails should she buy?
Answer:
The measure Trudy needs = 0.375
The inches in the hardware store measures nails = 125/1000; 25/100; 375/1000
Actually, the inches Trudy needs are given in the decimal form.
So that we need to find out the fraction form.
The fraction form is 375/1000
Therefore, Trudy should buy 375/1000.
Question 12.
It rained 16 hundredths of an inch on Tuesday. Write this amount as a decimal and a fraction.

Answer:
Actually, the word form is given
16 hundredths can be written as 16/100
In decimals, we can write it as 0.16
Therefore, 0.16 of an inch rained on Tuesday.
Question 13.
At Richardson Elementary, \(\frac{35}{100}\) of the buses were late because of a snowstorm. Write the fraction as a decimal.
Answer:
The above-given fraction is 35/100
Step 1: Find a number you can multiply by the bottom of the fraction to make it 10, 100, 1000, or any 1 followed by 0s.
– Step 2: Multiply both top and bottom by that number.
– Step 3. Then write down just the top number, putting the decimal point in the correct spot (one space from the right-hand side for every zero in the bottom number)
In decimals, we can write them as 0.35
Test Practice
Question 14.
Which of the following does not represent the number given by the model?

A. \(\frac{4}{10}\)
B. forty tenths
C. 0.4
D. four tenths
Answer: Option B is correct
It does not represent the above-given model.
The given model is the tenth cube
In fractions, we can write as 4/10
In decimals, we can write it as 0.4
In word form, we can write as four tenths.