All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 1 Lesson 2 Compare and Order Whole Number Through Millions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 1 Lesson 2 Compare and Order Whole Number Through Millions
Example 1
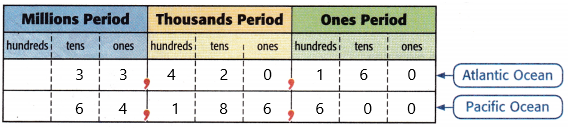
The table shows the two largest oceans in the world. Which ocean has a greater area?


Question 1.
Write the numbers in the place-value chart.
Answer:
Place value describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
Question 2.
Begin at the greatest place. Compare the digits.
6 ![]() 3
3
Since 6 is ______ than 3, then 64,186,600> 33,420,160.
So, the _____ has a greater area.
Answer:
Now compare the values.
Here asked which ocean has the greatest area.
6 > 3
Therefore, 64,186,600 > 33,420,160
Hence, the pacific ocean is greater than the Atlantic ocean.
Finally, the Pacific ocean has the greater area.
Example 2
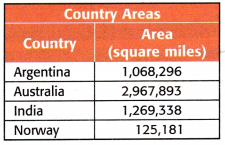
The table shows the area in square miles in different countries. Use place value to order the countries from greatest area to least area.
Answer:
The above-given country areas and their miles
The area of Argentina = 1,068,296
The area of Australia = 2,967,893
The area of India = 1,269,338
The area of Norway = 125,181
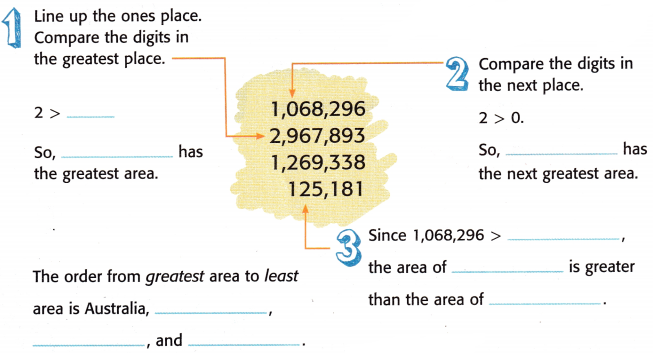
Now we need to order them in a greatest area to least area
compare the numbers
The greatest number is 2,967,893
The least number is 125,181
Now compare the 1,269,338 and 1,068,296
The first digit is same for both the numbers. Now check for the next left-most digit
2 > 0
After sorting all the numbers, the result will be:
2,967,893; 1,269,338; 1,068,296; 125,181
The countries are Australia; India; Argentina; Norway.
Talk Math
When ordering whole numbers, explain what to do when the digits in the same place have the same value.

Answer:
If the first two or three digits are the same, compare the next to determine the value of the numbers.
Guided Practice
Write <, >, or = in each ![]() to make a true sentence.
to make a true sentence.
Question 1.
655,543 ![]() 556,543
556,543
Answer: >
Explanation:
since both, the numbers are having the same number of digits
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
according to rule 2 compare the numbers
6 > 5
Hence we use the symbol greater than
655,543 > 556,543
Question 2.
10,027,301 ![]() 10,207,301
10,207,301
Answer: <
Explanation:
since both, the numbers are having the same number of digits
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
according to rule 2 compare the numbers
0 < 2
Hence, we use the symbol less than
10,027,301 < 10,207,301
Question 3.
Order the numbers 145,099; 154,032; 145,004; and 159,023 from greatest to least.
Answer:
For ordering the numbers from the greatest to lowest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
now compare the numbers. The first digit is the same in all the numbers.
5 > 4 and 9 > 4
The result will be:
159,023; 154,032; 145,099; 145,004
Independent Practice
Write <, >, or = in each ![]() to make a true sentence.
to make a true sentence.
Question 4.
462,211 ![]() 426,222
426,222
Answer:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
We go for rule 2.
The first digit is the same for both numbers. So check for the next left-most digits
6 > 2
So the first number is greater than the second number
Here, we use > symbol.
Therefore, 462,211 > 426,222
Question 5.
42,235,909 ![]() 42,324,909
42,324,909
Answer:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
We go for rule 2.
The first two digits are the same for both numbers. So check for the next left-most digits
2 < 3
So the first number is less than the second number
Here, we use < symbol
Therefore, 42,235,909 < 42,324,909
Question 6.
20,318,523 ![]() 21,318,724
21,318,724
Answer:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
We go for rule 2.
The first digit is the same for both numbers. So check for the next left-most digits
0 < 1
So the first number is less than the second number
Here, we use < symbol
Therefore, 20,318,523 < 21,318,724
Question 7.
96,042,317 ![]() 96,042,317
96,042,317
Answer:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
all the numbers are equal on both sides
96,042,317 = 96,042,317
The “equal to” symbol is used to represent two equal numbers or quantities.
Question 8.
132,721,424 ![]() 132,721
132,721
Answer:
In this problem, we are going to use rule 1:
When we compare numbers, then check if both the numbers are having the same number of digits or not. If a number has more digits, then it is greater than the other number.
Here, the first number is greater than second number
132,721,42 > 132,721
Question 9.
152,388,000 ![]() 152,388,010
152,388,010
Answer:
In this problem, we are going to use rule 2
This rule is applicable when two numbers are having the same number of digits. In such cases, we need to check the digit at the leftmost place, whichever is greater. Therefore, the number with a greater digit at the leftmost place of the number is greater than the other number.
The first seven digits are the same. So check for the next left-most digit
0 < 1
Hence, the first number is less than the second number
152,388,000 < 152,388,010
Question 10.
113,222,523 ![]() 113,333,523
113,333,523
Answer:
In this problem, we are going to use rule 2
This rule is applicable when two numbers are having the same number of digits. In such cases, we need to check the digit at the leftmost place, whichever is greater. Therefore, the number with a greater digit at the leftmost place of the number is greater than the other number.
The first three digits are the same. So check for the next left-most digit
2 < 3
Hence, the first number is less than the second number
Therefore, 113,222,523 < 113,333,523
Question 11.
767,676,767 ![]() 676,767,676
676,767,676
Answer:
In this problem, we are going to use rule 2
This rule is applicable when two numbers are having the same number of digits. In such cases, we need to check the digit at the leftmost place, whichever is greater. Therefore, the number with a greater digit at the leftmost place of the number is greater than the other number.
Check for the digits whose number is greater and lesser
7 > 6
Hence, the first number is greater than the second number.
Therefore, 767,676,767 > 676,767,676
Order the numbers from greatest to least.
Question 12.
138,023; 138,032; 139,006; 183,487
_____________________
Answer:
For ordering the numbers from the greatest to lowest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
The first digit is the same for all the numbers
Now check for the next left-most digit
8 < 9; 3 < 8
after sorting the numbers, the result will be:
183487, 139006, 138032, 138023
Question 13.
3,452,034; 4,935,002; 34,035,952; 34,530,953
_____________________
Answer:
since the numbers are having the same digits so check for the next left-most digit as per rule 2.
We can easily identify the greatest number
4 > 3
The greatest one is 4,935,002
now check for the first and third numbers: 5 > 0
now check for the first and final numbers: 3 > 2
after sorting the numbers, the result will be:
34530953, 34035952, 4935002, 3452034
Question 14.
731,364,898; 731,643,898; 73,264,898; 731,643,989
_____________________
Answer:
since the 731,364,898; 731,643,898 and 731,643,989 are having the same digits so check for the next left-most digit as per rule 2.
The number 73,264,898 is less compared to all the numbers
Now check for the above three numbers
The first three digits are the same so check for the next left-most digit
6 > 3
and check for the second and fourth numbers: 9 > 8
after sorting the numbers, the result will be:
731643989, 731643898, 731364898, 73264898
Question 15.
395,024,814; 593,801,021; 395,021,814; 39,021,814
_____________________
Answer:
We can find out the greatest number easily
compare the numbers
5 > 3
The greatest number is 593,801,021
The least number is 39,021,814
Now compare the first and third numbers
4 > 1
After sorting the numbers, the result will be:
593,801,021; 395,024,814; 395,021,814; 39,021,814
Order the numbers from least to greatest.
Question 16.
85289688; 85,290,700; 85,285,671; 85,301,001
_____________________
Answer:
For ordering the numbers from least to greatest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
The first two digits are the same. So compare the next left-most digit.
3 > 2
The greatest one is 85,301,001
Now compare the next left-most digit
9 > 8
The second greatest one is 85,290,700
after sorting the numbers the result will be:
85285671, 85289688, 85290700, 85301001
Question 17.
32,356,800; 33,353,800; 32,937,458; 33,489,251
_____________________
Answer:
For ordering the numbers from least to greatest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
The first digit is the same now check for the next left-most digit
After sorting the numbers the result will be:
32356800, 32937458, 33353800, 33489251
Question 18.
2,009,146; 2,037,579; 2,006,981; 2,011,840
_____________________
Answer:
For ordering the numbers from least to greatest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
The first two digits are the same now check for the next left-most digit.
0 < 3; likewise, check all the digits
In the first and third numbers, check for the fourth digit: 9 > 6
after sorting the numbers:
2006981, 2009146, 2011840, 2037579
Question 19.
854,236,100; 855,963,250; 855,903,675; 854,114,370
_____________________
Answer:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
The first two digits are the same now check for the next left-most digit.
In the first and last numbers, check the fourth digit: 2 < 1
For the second and third numbers, check the fifth digit: 6 > 0
after sorting the numbers, the result will be:
854114370, 854236100, 855903675, 855963250
Problem Solving
Question 20.
Rank the following states from least to greatest population.
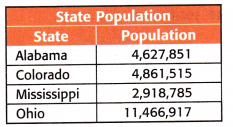
Answer:
The population of Alabama = 4,627,851
The population of Colorado = 4,861,515
The population of Mississippi = 2,918,785
The population of Ohio = 11,466,917
Now compare all the numbers.
The least one is 2,918,785
The greater one is 11,466,917
Now we need to compare the 4,627,851 and 4,861,515
The first digit is the same and needs to check the next left-most digit
6 < 8
After the sorting of numbers, the result will be:
2,918,785; 4,627,851; 4,861,515; 11,466,917
Question 21.
Order the cars from most expensive to least expensive.
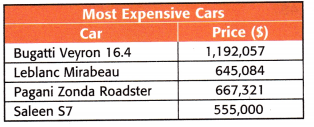
Answer:
The expensive Bugatti Veyron 16.4 = 1,192,057
The expensive Leblanc Mirabeau = 645,084
The expensive Pagani Zonda Roadster = 667,321
The expensive Saleen S7 = 555,000
The most expensive car is 1,192,057 according to rule 1.
The least expensive car is 555,000
Now compare the 645,084 and 667,321
The first digit is the same and now check the next left-most digit
4 < 6
After sorting the numbers the result will be:
1,192,057; 667,321; 645,084; 555,000
Hot Problems
Question 22.
Mathematical PRACTICE 2 Reason Write three numbers that are greater than 75,300,000 but less than 75,400,000.
Answer:
75300100, 75300200, 75300900
we can compare the above numbers with the above-given numbers by using certain rules.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
Rule 1: Numbers with more digits
When we compare numbers, then check if both the numbers are having the same number of digits or not. If a number has more digits, then it is greater than the other number.
Rule 2: Numbers starting with a larger digit
This rule is applicable when two numbers are having the same number of digits. In such cases, we need to check the digit at the leftmost place, whichever is greater. Therefore, the number with a greater digit at the leftmost place of the number is greater than the other number.
Question 23.
? Building on the Essential Question How do you compare whole numbers through the millions?
Answer:
A positive number is greater than a negative number. If both numbers are positive, the longer number – the one with more digits – is larger. If both have the same number of digits, compare the digits from the left, one at a time until you find one that is different. The one with the larger digit in this last comparison is the larger number.
or
You can compare numbers through the millions by looking at the value of each digit starting at the millions place of each number.
McGraw Hill My Math Grade 5 Chapter 1 Lesson 2 My Homework Answer Key
Practice
Write <, >, or = in ![]() to make a true sentence.
to make a true sentence.
Question 1.
67,982,001 ![]() 67,892,001
67,892,001
Answer: >
Explanation:
We need to compare the numbers.
we go for rule 2
since both, numbers are having the same number of digits. We will compare the next left-most digits.
Here, the first two digits are the same then check for the next left-most digit.
9 > 8
So we use a symbol greater than.
Therefore, 67982001 > 67892001
Question 2.
100,542,089 ![]() 105,042,098
105,042,098
Answer: <
Explanation:
We need to compare the numbers.
we go for rule 2
since both, numbers are having the same number of digits. We will compare the next left-most digits.
Here, the first two digits are the same then check for the next left-most digit.
0 < 5
So we use a symbol less than.
Therefore, 100542089 < 105042098
Question 3.
1,986,034 ![]() 1,896,075
1,896,075
Answer: >
We need to compare the numbers.
we go for rule 2
since both, numbers are having the same number of digits. We will compare the next left-most digits.
Here, the first digit is the same then check for the next left-most digit.
9 > 8
so we use a symbol greater than.
Therefore, 1986034 > 1896075
Question 4.
12,165,982 ![]() 12,178,983
12,178,983
Answer: <
Explanation
We need to compare the numbers.
we go for rule 2
since both, numbers are having the same number of digits. We will compare the next left-most digits.
Here, the first three digits are the same then check for the next left-most digit.
6 < 7
So we use a symbol less than.
Therefore, 12165982 < 12178983
Question 5.
239,742,005 ![]() 289,650,010
289,650,010
Answer: <
Explanation:
We need to compare the numbers.
we go for rule 2
since both, numbers are having the same number of digits. We will compare the next left-most digits.
Here, the first digit is the same then check for the next left-most digit.
3 < 8
So we use a symbol less than
Therefore, 239742005 < 289650010
Question 6.
1,652,985 ![]() 1,563,218
1,563,218
Answer: >
Explanation
We need to compare the numbers.
we go for rule 2
since both, numbers are having the same number of digits. We will compare the next left-most digits.
Here, the first digit is the same then check for the next left-most digit.
6 > 5
so we use a symbol greater than
Therefore, 1652985 > 1563218
Order the numbers from greatest to least
Question 7.
3,356,000; 2,359,412; 2,937,158; 3,368,742
Answer:
For ordering the numbers from the greatest to lowest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
3 > 2
The first two numbers are starting with 3.
3356000, 3368742
Now find the greatest one in that two numbers.
The third digits are 6 and 5
6 > 5
So here, the greatest number is: 3368742
Now check for the least number:
2359412, 2937158
The first two digits are the same. Now check for the second left-most digit
3 < 9
So the least number is 2359412
After sorting the numbers, the result will be:
3368742, 3356000, 2937158, 2359412
Question 8.
2,009,832; 2,103,425; 2,009,604; 2,112,300
Answer:
For ordering the numbers from the greatest to lowest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
0 < 1
The two greatest numbers are 2103425, 2112300
Now find the greatest number:
1 > 0
2112300 is the greatest number and the second greatest number is 2103425
And the remaining two numbers are 2009832, 2009604
The first four numbers are the same, now compare the next left-most digit
8 > 6
After sorting all the numbers the result will be:
2112300, 2103425, 2009832, 2009604
Order the numbers from least to greatest.
Question 9.
14,258,123; 14,259,688; 14,256,001; 14,258,252
Answer:
For ordering the numbers from least to greatest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
The first four digits are the same. So compare the next left-most digit.
8 < 9 < 6 > 8
After sorting the numbers 14258123, 14259688, 14256001, and 14258252 from Least to Greatest, the result will be
14256001,14258123,14258252,14259688.
Question 10.
574,210,033; 574,211,874; 574,198,852; 874,210,089
Answer:
For ordering the numbers from least to greatest we need to compare.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
All the numbers having the same number of digits
The first four digits are the same. So compare the next left-most digit.
5 = 5 = 5 > 8
So the greatest number is 874,210,089
The next two digits are equal in all numbers.
Now compare the next left-most digits.
2 = 2 = 2 < 1
The smallest digit is 574198852
After sorting the numbers, the result will be:
574198852, 574210033, 574211874, 874210089
Problem Solving
Question 11.
Madison wants to know which sports are most popular. The list below shows how many kids play each sport. Order the sports from most players to least players to help show Madison which sports are most popular.
Soccer: 3,875,026 Surfing: 250,982
Bašeball: 900,765 Basketball: 2,025,351

Answer:
Above-given:
The kids play Soccer = 3,875,026
The kids play Surfing = 250,982
The kids play Baseball = 900,765
The kids play Basketball = 2,025,351
We need to order them in more to fewer
For that, we need to compare the numbers
3875026 and 2025351 are having the same number of digits. The number of digits is 7.
250982 and 900765 are having the same number of digits. The number of digits is 6.
The order will be:
3875026, 2025351, 900765, 250982
The most popular sport is Soccer because it is having the highest number of players.
Question 12.
Andrea wants to live in the city with the most people. She read that New York City has 8,008,278 people and that Seoul, South Korea has 10,231,217 people. In which city does Andrea want to live?
Answer:
The number of people in New York City = 8,008,278
The number of people in South Korea = 10,231,217
Andrea will live in the city which is having the highest population.
Now we compare the numbers.
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
We go for rule 1 because 8,008,278 has 7 digits and 10,231,217 has 8 digits.
– therefore, according to rule 1, the number with more digits is greater than the number with fewer digits.
Hence, South Korea is having the highest population. Therefore, Andrea lives in South Korea.
Question 13.
The Denver Mint made 2,638,800 nickels. The Philadelphia Mint made 2,806,000 nickels. Which mint made more nickels?
Answer:
Above-given:
The nickels made by Denver mint = 2,638,000
The nickels made by Philadelphia mint = 2,806,000
We need to find out the number of more nickels made by mints.
Now we need to compare the numbers.
Since, both the numbers, 2638000 and 2806000 are having 7 digits, thus we will compare the left-most digit of both numbers.
– the first digits are the same in both numbers. So we will compare the next left-most digit
6 < 8
so, the Denver mint made fewer nickels than the Philadelphia mint.
Finally, the Philadelphia mint made more nickels.
Question 14.
Mathematical PRACTICE 3 Draw a Conclusion In 1950, bike stores sold about 205,850 bikes per year per store. In 2000, bike stores sold about 185,000 bikes per year per store. Is the number of bikes being sold getting larger or smaller?
Answer:
The bikes sold in 1950 = 205,850
The bikes sold in 2000 = 185,000
The bikes sold getting smaller
185,000 < 205,850
as year is increasing, bikes sold are decreasing.
Test Practice
Question 15.
Which set of numbers is in order from greatest to least?
A. 74,859,623; 74,759,458; 74,905,140; 73,569,991
B. 74,905,140; 74,859,623; 74,759,458; 73,569,991
C. 73,569,991; 74,759,458; 74,859,623; 74,905,140
D. 74,905,140; 74,759,458; 74,859,623; 73,569,991
Answer: Option B is correct
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
If we take the set of numbers in option A,
The first two numbers are the same so we will compare the next left-most digits
8 < 7 > 9 there is no certain order.
coming to option B:
the least number is in the last position. Now check for the first three numbers.
The first two numbers are the same so we will compare the next left-most digits
9 < 8 < 7
Therefore, option B is having correct order.