All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 1 Place Value will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 1 Place Value
Essential Question
How does the position of a digit in a number relate to its value?
Answer:
The position of each digit in a number determines the value. Except for 0, which has a zero value in any position in the number, when a digit changes its position, its place value also changes, therefore changing the value of the number.
Example:
Take the numbers 1, 2, 3, 4
In number 1234, the place value of 3 is tens place.
In the number 1324, the place of 3 in a hundred place.
Am I Ready?
Write each number in word form.
Question 1.
8 ________
Answer: Eight
How to write numbers in words:
There are certain rules to writing the numbers in words. To write any number in the form of words, we have to check the place value. Let us learn this by observing the below steps.
– The place value of one’s, a number from 1 to 9 is written in words as, one, two, three, four, five, six, seven, eight and nine.
– The least number which is at tens place is 10, which is written in words as ten.
The above-given question was in one’s number and the number was 8.
– Then it will be written as eight.
Question 2.
23 _____
Answer:
By following the below steps we can write 23 as:
Twenty-three
Explanation:
There are certain rules to writing the numbers in words. To write any number in the form of words, we have to check the place value. Let us learn this by observing the below steps.
– The place value of one’s, a number from 1 to 9 is written in words as, one, two, three, four, five, six, seven, eight and nine.
– The least number which is at tens place is 10, which is written in words as ten.
– The numbers 11 to 19 are written in words as, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen and nineteen. And the next number is twenty.
– After twenty, the numbers follow the pattern in such a way that they are written in words such as thirty, forty, fifty, sixty, seventy, eighty, ninety and so on.
– The preceding numbers are linked with these words and mentioned from one to nine. For example, twenty-one, twenty-two, etc.
Question 3.
15 ________
Answer: fifteen
Explanation:
There are certain rules to writing the numbers in words. To write any number in the form of words, we have to check the place value. Let us learn this by observing the below steps.
– The numbers 11 to 19 are written in words as, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen and nineteen. And the next number is twenty.
Question 4.
160 _____
Answer:
The above-given number is 160.
According to the rules, 160 can be written as one hundred and sixty.
In the number 160, 0 is in one’s place so there is no one’s place.
6 is in the ten’s place so there are 6 tens (60)
and 1 is in the hundreds place so there are 1 hundred.
Write the number that represents each point on the number line.

Question 5.
Q _____
Answer:
A number line can be defined as a straight line with numbers placed at equal intervals or segments along its length. A number line can be extended infinitely in any direction and is usually represented horizontally. The numbers on the number line increase as one moves from left to right and decrease on moving from right to left.
In the number line, the point Q represents the number 2.
Question 6.
S _____
Answer:
A number line can be defined as a straight line with numbers placed at equal intervals or segments along its length. A number line can be extended infinitely in any direction and is usually represented horizontally. The numbers on the number line increase as one moves from left to right and decrease on moving from right to left.
In the number line, the point S represents the number 8.
Question 7.
R _____
Answer:
A number line can be defined as a straight line with numbers placed at equal intervals or segments along its length. A number line can be extended infinitely in any direction and is usually represented horizontally. The numbers on the number line increase as one moves from left to right and decrease on moving from right to left.
In the number line, the point R represents the number 5.
Question 8.
T _____
Answer:
A number line can be defined as a straight line with numbers placed at equal intervals or segments along its length. A number line can be extended infinitely in any direction and is usually represented horizontally. The numbers on the number line increase as one moves from left to right and decrease on moving from right to left.
In the number line, the point T represents the number 12.
Question 9.
V _____
Answer:
A number line can be defined as a straight line with numbers placed at equal intervals or segments along its length. A number line can be extended infinitely in any direction and is usually represented horizontally. The numbers on the number line increase as one moves from left to right and decrease on moving from right to left.
In the number line, the point V represents the number 1.
Question 10.
W _____
Answer:
A number line can be defined as a straight line with numbers placed at equal intervals or segments along its length. A number line can be extended infinitely in any direction and is usually represented horizontally. The numbers on the number line increase as one moves from left to right and decrease on moving from right to left.
In the number line, the point W represents the number 15.
Write each sentence using the symbols <, >, or =.
Question 11.
8 is less than 12.
__________
Answer:
According to the given question, the sentence will be:
8 < 12
The “less than” symbol is used when a number or a quantity is less than the other.
A smaller number less than a greater number is represented as:
Smaller Number < Greater Number
Question 12.
24 is greater than 10.
Answer:
According to the given question, the sentence will be:
24 > 10
The “greater than” symbol is used to show if a number is greater than the other number.
A bigger number greater than a smaller number is represented as:
Bigger Number > Smaller Number
Question 13.
The high-temperature yesterday was 64°F. The high-temperature today is 70°F. Write 64 is less than 70 using the symbols <>, or =.
Answer:
The above-given question:
The temperature recorded yesterday = 64°F
The temperature recorded today = 70°F
Now we need to compare both the values using the comparison symbols.
64 < 70
The “less than” symbol is used when a number or a quantity is less than the other.
A smaller number less than a greater number is represented as:
Smaller Number < Greater Number
How Did I Do?
Shade the boxes to show the problems you answered correctly.
![]()
My Math Words
Review Vocabulary
comma hundreds hundred thousand ones
tens ten thousand thousand
Making Connections
Use the review words to complete each section of the bubble map.
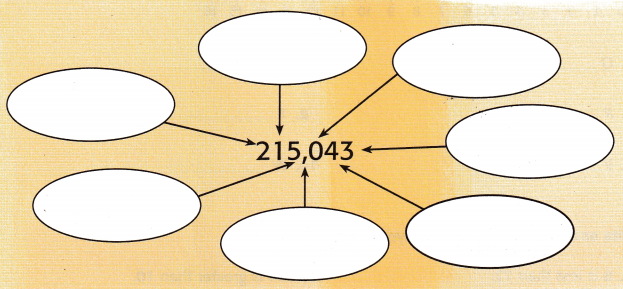
Describe how commas are used in writing greater numbers.
_____________________
_____________________
_____________________
_____________________
Answer:
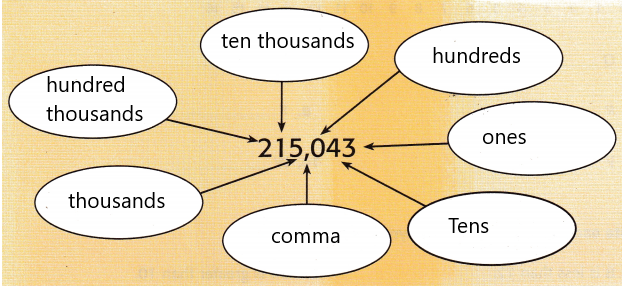
“Use of Commas” when the numbers are large. When we write or read large numbers, then commas are used. But we do not use commas while writing the names of numbers.
Rules of using commas:
There are certain rules for using commas between the digits of large numbers. They are:
– For a large number, the first comma has to be placed after hundreds place (that means three digits from the right of the given number). This comma marks thousands.
– The second comma will come after the next two digits (that means five digits from the right of the given number). This comma comes past ten thousand places and marks lakh.
– The third comma will come after the next two digits (that means seven digits from the right of the given number). This comma comes after ten lakh places and marks crore.
My Vocabulary Cards
Mathematical Practice
Ideas for Use
- Design a crossword puzzle. Use the definition for each word as the clues.
- Work with a partner to name the part of speech of each word. Consult a dictionary to check your answers.
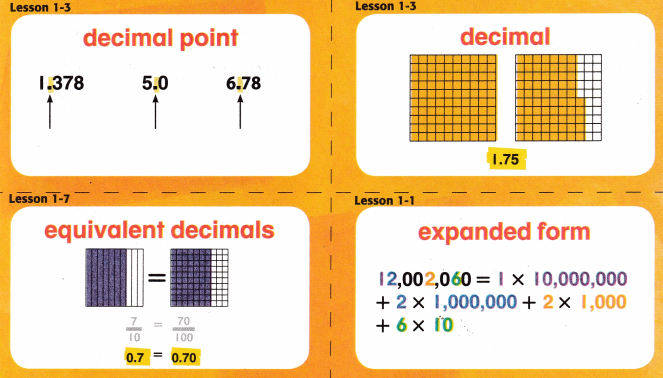
A number that has a digit in the tenths place, hundredths place, and/or beyond.
Erin ate \(\frac{3}{4}\) of a sandwich. Write the amount eaten as a decimal.
Answer:
The amount of sandwich Erin ate = 3/4
3/4th can be written as 0.75
If we refer to the decimal place value chart, then 0 is in the one place. So 0 x 1 = 0
Now, let us check the place value of 7. We can see that 7 comes under the tenths column. Therefore, the place value of 7 is 7 tenths, which means 7/10, or, 0.7
Now, we check for the place value of 5. We see that 5 comes under the hundredths column, therefore, the place value of 5 is 5 hundredths, or 5/100 = 0.05
A period separating the ones and the tenths in a decimal number.
How does a number with a decimal point differ from a number without one?
Answer:
True, a decimal number is made up of a whole number and a fractional part that is separated by a dot called the decimal point.
The decimal place value chart is a chart that shows the place values of all the digits in a given decimal number. The digits to the left of the decimal points represent the place values starting from ones, followed by tens, hundreds, thousands, and so on. The digits to the right of the decimal points represent the place values starting from tenths, followed by hundredths, thousandths, and so on.
A way of writing a number as the sum of the values of its digits.
Expand can mean “to stretch or unfold.” How can this definition help you remember this definition?
Answer: Expanded form.
The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Go through the below steps to write the numbers in expanded form:
Step 1: Get the standard form of the number.
Step 2:Identify the place value of the given number using the place value chart.
Step 3: Multiply the given digit by its place value and represent the number in the form of (digit × place value).
Step 4: Finally, represent all the numbers as the sum of (digit × place value) form, which is the expanded form of the number.
Decimals that have the same value.
Name two topics in math that can be described as equivalent.
Answer:
Two decimals are equivalent when they have the same value. For example, by showing that 0.3, 0.30, and 0.300 covers the same space, we can see that these two decimals have the same value. Hence, these are equivalent decimals. If we add zeros at the end of a decimal number, the value of a decimal number will not change.
Rules to identify equivalent decimals:
– checking the place value of the digits of the decimal numbers.
– converting the decimal numbers into fractions
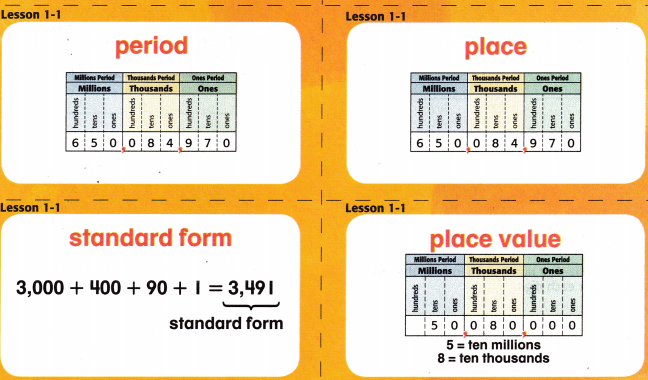
The position of a digit in a number.
What is ä synonym for place?
Answer:
Place value describes the position of a digit in a given number and the value it has. The value of a digit changes when the place or position of the digit changes. Every digit in a number has a value.
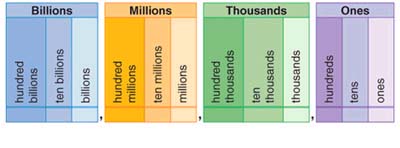
The name was given to each group of three digits in a place-value chart.
What is the meaning of period in language arts?
Answer: Periods
Each digit in a given number has a place value.
When a number is written in standard form, each group of digits separated by a comma is called a period. The number 5,913,603,800 has four periods. Each period is shown by a different colour in the place value chart.
The period (also known as a full stop, especially in British English) is a punctuation mark ( . ) primarily used to indicate the end of a sentence. It appears as a single dot on the bottom line of the text, and it comes immediately after the last word of the sentence without a space.
The value is given to a digit by its place in a number.
Write a six-digit number. Then write the place value for each digit.
Answer: Place value.
Place value is the value of each digit in a number. The value of every digit in a number is different based on its position. A number might have two similar digits but different values, which is decided by the position that the digit holds in the number.
For example, if we take the 6-digit number
The six-digit number is 123456
6 is in the one’s place; 5 is in the tens place
4 is in the hundreds place; 3 is in the thousands place
2 is in the ten thousand places; 1 is in the hundred thousand places.
The usual way of ng a number that shows only its digits, no words.
Write a different meaning of the word standard.
Answer:
Standard form
A standard form of a number in Maths is basically mentioned for the representation of large numbers or small numbers. We use exponents to represent such numbers in standard form.
We can say standard means commonplace.
My Vocabulary Cards
Mathematical Practices

Ideas for Use
- Use a blank card to write this chapter’s essential question. Use the back of the card to write or draw examples that help you answer the question.
- Use blank cards to review key concepts from the chapter. Write a few study tips on the back of each card.


My Foldable.
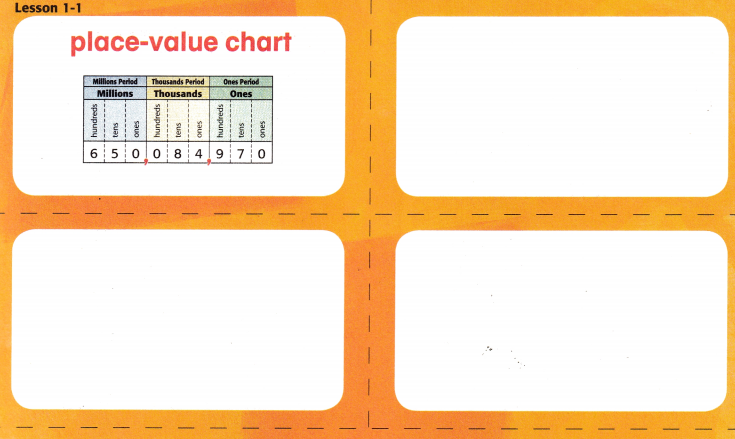
Answer:
The above-given number: 7,932,035
Place value describes the value of every digit in a number depending on its position. These positions start from the unit’s place (one’s place). The order of the place value of digits in a number from right to left is expressed as ones/units, tens, hundreds, thousands, ten thousand, and so on.
– The chart has the number 7,932,035 on it. Each digit in the number 7,932,035 will have a different value.
– The digit 5 is in the place and it has a value of 5 × 1 = 5
– The digit 3 is in the tens place and it has a value of 3 × 10 = 30
– The digit 0 is in the hundreds place and it has a value of 0 × 100 = 0
– The digit 2 is in the thousands place and it has a value of 2 × 1000 = 2000
– The digit 3 is in the ten thousand places and it has a value of 3 × 10000 = 30000
– The digit 9 is in the one hundred thousand places and it has a value of 9 × 100000 = 900000
– The digit 7 is in the millions place and it has a value of 7 × 1000000 = 7000000
Foldables
Follow the steps on the back to make your Foldable.
9 ___ ___, ___ ___ ___, ___ ___ ___
hundred
millions
Answer:
9 hundred million can be written as:
900,000,000
8 ___, ___ ___ ___, ___ ___ ___
ten
millions
Answer:
8 ten million can be written as:
80,000,000
7, ___ ___ __‚ ___ ___ ___
millions
Answer:
7 million can be written as:
7,000,000
6 ___ ___, ___ ___ ___
hundreds
thousands
Answer:
6 hundred thousand can be written as:
600,000
5 ___, ___ ___ ___
ten
thousands
Answer:
5 ten thousand can be written as:
50,000
Foldables
Study Organizer
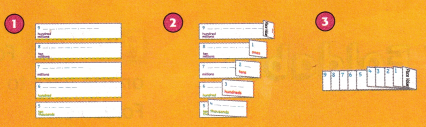
Place Value
1
ones
2 _____
tens
3 ___ ____
hundreds
4, ____ ___ ___
thousands
Answer:
The above-given numbers 1, 2, 3, 4
The number we can write as:
4321
4 is in the thousands place [4,000]
3 is in the hundreds place [300]
2 is in the tens place [20]
1 is in the one’s/units place. [1]