All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 9 Lesson 2 Add Like Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 9 Lesson 2 Add Like Fractions
Think of adding like fractions as joining parts that refer to the same whole. To add like fractions, add the numerators and keep the same denominator.
\(\frac{1}{5}\) + \(\frac{2}{5}\) = \(\frac{3}{5}\)
\(\frac{3}{10}\) + \(\frac{4}{10}\) = \(\frac{7}{10}\)
Math in My World
Example 1
Pablo spent \(\frac{2}{6}\) of an hour on a jigsaw puzzle. Conrad spent \(\frac{1}{6}\) of an hour on the puzzle. How much time did they spend working on the puzzle in all?

Find \(\frac{2}{6}\) + \(\frac{1}{6}\).
1. Add the numerators. Keep the same denominator.
\(\frac{2}{6}\) + \(\frac{1}{6}\) = \(\frac{2+1}{6}\)
= \(\frac{3}{6}\)
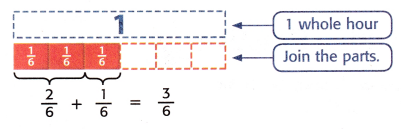
2. Write the sum in the simplest form.

So, they spent ![]() hour on the puzzle.
hour on the puzzle.
Answer:
Number of hours they spend working on the puzzle in all = \(\frac{1}{2}\) 
Explanation:
Number of hours Pablo spent on a jigsaw puzzle = \(\frac{2}{6}\)
Number of hours Conrad spent on the puzzle = \(\frac{1}{6}\)
Number of hours they spend working on the puzzle in all = Number of hours Pablo spent on a jigsaw puzzle + Number of hours Conrad spent on the puzzle
= \(\frac{2}{6}\) + \(\frac{1}{6}\)
= [(2 + 1) ÷ 6]
= \(\frac{3}{6}\) ÷ \(\frac{3}{3}\)
= \(\frac{1}{2}\)
Example 2
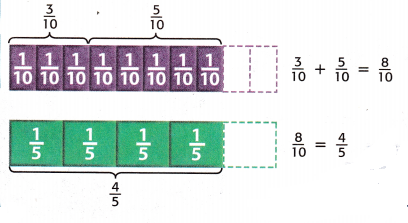
Find \(\frac{3}{10}\) + \(\frac{5}{10}\).
Helpful Hint
To simplify a fraction, divide the numerator and denominator by the greatest common factor.
1. Add
\(\frac{3}{10}\) + \(\frac{5}{10}\). = \(\frac{3+5}{10}\)
= \(\frac{8}{10}\)
2. Simplify
![]()
So, \(\frac{3}{10}\) + \(\frac{5}{10}\) = ![]() .
.
Check: Use models to check.
Answer:
Sum of \(\frac{3}{10}\) and \(\frac{5}{10}\) = \(\frac{4}{5}\)
Explanation:
\(\frac{3}{10}\) + \(\frac{5}{10}\) = ??
Sum of \(\frac{3}{10}\) + \(\frac{5}{10}\) = [(3 + 5) ÷ 10]
= \(\frac{8}{10}\) ÷ \(\frac{2}{2}\)
= \(\frac{4}{5}\)

Talk Math
Describe two ways to decompose \(\frac{4}{5}\) into a sum.

Answer:
Decomposition of \(\frac{4}{5}\) into a sum:
One way:
\(\frac{4}{5}\) = \(\frac{3}{5}\) + \(\frac{1}{5}\)
Second way:
\(\frac{4}{5}\) = \(\frac{2}{5}\) + \(\frac{2}{5}\)
Explanation:
Two ways to decompose \(\frac{4}{5}\) into a sum:
One way:
\(\frac{4}{5}\) = \(\frac{3}{5}\) + \(\frac{1}{5}\)
= [(3 + 1) ÷ 5]
= \(\frac{4}{5}\)
Second way:
\(\frac{4}{5}\) = \(\frac{2}{5}\) + \(\frac{2}{5}\)
= [(2 + 2) ÷ 5]
= \(\frac{4}{5}\)
Guided Practice
Find each sum. Write in simplest form.
Question 1.
\(\frac{1}{6}\) + \(\frac{2}{6}\) = ![]()
Answer:
\(\frac{1}{6}\) + \(\frac{2}{6}\) = 
Explanation:
Sum of \(\frac{1}{6}\) + \(\frac{2}{6}\):
= [(1 + 2) ÷ 6]
= \(\frac{3}{6}\) ÷ \(\frac{3}{3}\)
= \(\frac{1}{2}\)
Question 2.
\(\frac{2}{5}\) + \(\frac{2}{5}\) = ![]()
Answer:
\(\frac{2}{5}\) + \(\frac{2}{5}\) = 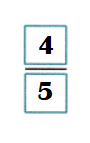
Explanation:
Sum of \(\frac{2}{5}\) + \(\frac{2}{5}\):
= [(2 + 2) ÷ 5]
= \(\frac{4}{5}\)
Independent Practice
Find each sum. Write in simplest form.
Question 3.
\(\frac{1}{3}\) + \(\frac{1}{3}\) = _________________
Answer:
\(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\)
Explanation:
Sum of \(\frac{1}{3}\) and \(\frac{1}{3}\):
=> \(\frac{1}{3}\) + \(\frac{1}{3}\)
=> [(1 + 1) ÷ 3]
=> \(\frac{2}{3}\)
Question 4.
\(\frac{2}{6}\) + \(\frac{3}{6}\) = _________________
Answer:
\(\frac{2}{6}\) + \(\frac{3}{6}\) = \(\frac{5}{6}\)
Explanation:
Sum of \(\frac{2}{6}\) and \(\frac{3}{6}\):
=> \(\frac{2}{6}\) + \(\frac{3}{6}\) =
=> [(2 + 3) ÷ 6]
=> \(\frac{5}{6}\)
Question 5.
\(\frac{3}{8}\) + \(\frac{1}{8}\) = _________________
Answer:
\(\frac{3}{8}\) + \(\frac{1}{8}\) = \(\frac{1}{2}\)
Explanation:
Sum of \(\frac{3}{8}\) and \(\frac{1}{8}\):
=> \(\frac{3}{8}\) + \(\frac{1}{8}\) =
=> [(3 + 1) ÷ 8]
=> \(\frac{4}{8}\) ÷ \(\frac{4}{4}\)
=> \(\frac{1}{2}\)
Question 6.
\(\frac{5}{8}\) + \(\frac{2}{8}\) = _________________
Answer:
\(\frac{5}{8}\) + \(\frac{2}{8}\) = \(\frac{7}{8}\)
Explanation:
Sum of \(\frac{5}{8}\) and \(\frac{2}{8}\):
=> \(\frac{5}{8}\) + \(\frac{2}{8}\) =
=> [(5 + 2) ÷ 8]
=> \(\frac{7}{8}\)
Question 7.
\(\frac{3}{10}\) + \(\frac{7}{10}\) = _________________
Answer:
\(\frac{3}{10}\) + \(\frac{7}{10}\) = 1.
Explanation:
Sum of \(\frac{3}{10}\) and \(\frac{7}{10}\):
=> \(\frac{3}{10}\) + \(\frac{7}{10}\)
=> [(3 + 7) ÷ 10]
=> \(\frac{10}{10}\) ÷ \(\frac{10}{10}\)
=> 1.
Question 8.
\(\frac{2}{5}\) + \(\frac{1}{5}\) = _________________
Answer:
\(\frac{2}{5}\) + \(\frac{1}{5}\) = \(\frac{3}{5}\)
Explanation:
Sum of \(\frac{2}{5}\) and \(\frac{1}{5}\):
=> \(\frac{2}{5}\) + \(\frac{1}{5}\)
=> [(2 + 1) ÷ 5]
=> \(\frac{3}{5}\)
Question 9.
\(\frac{2}{12}\) + \(\frac{5}{12}\) = _________________
Answer:
\(\frac{2}{12}\) + \(\frac{5}{12}\) = \(\frac{7}{12}\)
Explanation:
Sum of \(\frac{2}{12}\) and \(\frac{5}{12}\):
=> \(\frac{2}{12}\) + \(\frac{5}{12}\)
=> [(2 + 5) ÷ 12]
=> \(\frac{7}{12}\)
Question 10.
\(\frac{1}{4}\) + \(\frac{2}{4}\) = _________________
Answer:
\(\frac{1}{4}\) + \(\frac{2}{4}\) = \(\frac{3}{4}\)
Explanation:
Sum of \(\frac{1}{4}\) and \(\frac{2}{4}\):
=> \(\frac{1}{4}\) + \(\frac{2}{4}\)
=> [(1 + 2) ÷ 4]
=> \(\frac{3}{4}\)
Question 11.
\(\frac{1}{6}\) + \(\frac{2}{6}\) = _________________
Answer:
\(\frac{1}{6}\) + \(\frac{2}{6}\) = \(\frac{1}{2}\)
Explanation:
Sum of \(\frac{1}{6}\) and \(\frac{2}{6}\):
=> \(\frac{1}{6}\) + \(\frac{2}{6}\)
=> [(1 + 2) ÷ 6]
=> \(\frac{3}{6}\) ÷ \(\frac{3}{3}\)
=> \(\frac{1}{2}\)
Algebra Write each fraction as a sum of unit fractions. Then write an equation to decompose the fraction in a different way.
Question 12.
\(\frac{4}{5}\)
Answer:
\(\frac{4}{5}\) = \(\frac{1}{5}\)+ \(\frac{1}{5}\)+ \(\frac{1}{5}\)+ \(\frac{1}{5}\) = \(\frac{2}{5}\) + \(\frac{2}{5}\)
Explanation:
Fraction as a sum of unit fractions:
\(\frac{4}{5}\) = \(\frac{1}{5}\)+ \(\frac{1}{5}\)+ \(\frac{1}{5}\)+ \(\frac{1}{5}\)
Decomposition of \(\frac{4}{5}\) = \(\frac{2}{5}\) + \(\frac{2}{5}\)
Question 13.
\(\frac{3}{4}\)
Answer:
\(\frac{3}{4}\) = \(\frac{1}{4}\)+ \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\) + \(\frac{1}{4}\)
Explanation:
Fraction as a sum of unit fractions:
\(\frac{3}{4}\)= \(\frac{1}{4}\)+ \(\frac{1}{4}\) + \(\frac{1}{4}\)
Decomposition of \(\frac{3}{4}\) = \(\frac{2}{4}\) + \(\frac{1}{4}\)
Question 14.
\(\frac{3}{8}\)
Answer:
\(\frac{3}{8}\) = \(\frac{1}{8}\)+ \(\frac{1}{8}\)+ \(\frac{1}{8}\) = \(\frac{1}{8}\) + \(\frac{2}{8}\)
Explanation:
Fraction as a sum of unit fractions:
\(\frac{3}{8}\) = \(\frac{1}{8}\)+ \(\frac{1}{8}\)+ \(\frac{1}{8}\)
Decomposition of \(\frac{3}{8}\) = \(\frac{1}{8}\) + \(\frac{2}{8}\)
Problem Solving
Question 15.
Marcela ate \(\frac{4}{10}\) of a box of crackers last week. Then she ate \(\frac{2}{10}\) of the box of crackers this week. What fraction of the box of crackers did Marcela eat altogether? Write in simplest form.

Answer:
Fraction of the box of crackers Marcela eat altogether = \(\frac{3}{5}\)
Explanation:
Quantity of a box of crackers last week Marcela ate = \(\frac{4}{10}\)
Quantity of a box of crackers this week Marcela ate = \(\frac{2}{10}\)
Fraction of the box of crackers Marcela eat altogether = Quantity of a box of crackers last week Marcela ate + Quantity of a box of crackers this week Marcela ate
= \(\frac{4}{10}\) + \(\frac{2}{10}\)
= [(4 + 2) ÷ 10]
= \(\frac{6}{10}\) ÷ \(\frac{2}{2}\)
= \(\frac{3}{5}\)
Question 16.
Greyson’s mom used 4 out of 12 eggs to make pancakes. Then she used 3 out of 12 eggs to make cupcakes. What fraction of a dozen eggs did she use in all? (Hint: 1 dozen = 12)
Answer:
Fraction of a dozen eggs did she use in all = \(\frac{7}{12}\)
Explanation:
Number of eggs Greyson’s mom used to make pancakes = 4.
Total number of eggs to make pancakes = 12.
Number of eggs later Greyson’s mom used to make pancakes = 3.
Fraction of a dozen eggs did she use in all = (Number of eggs Greyson’s mom used to make pancakes + Number of eggs later Greyson’s mom used to make pancakes) ÷ Total number of eggs to make pancakes
= (4 + 3) ÷ 12
= 7 ÷ 12 or \(\frac{7}{12}\)
Question 17.
Mathematical PRACTICE Model Math Bryce has to complete 100 minutes of writing every ten days. He writes for 10 minutes each day. What fraction of his writing requirement does Bryce complete in five days? Write in simplest form.
Answer:
Fraction of his writing requirement Bryce complete in five days = \(\frac{1}{2}\)
Explanation:
Number of minutes of writing every ten days Bryce has to complete = 100 .
Number of minutes each day he writes = 10.
Fraction of his writing requirement Bryce complete in five days = (5 × Number of minutes each day he writes) ÷ Number of minutes of writing every ten days Bryce has to complete
= (5 × 10) ÷ 100
= 50 ÷ 100 or \(\frac{50}{100}\)
= \(\frac{50}{100}\) ÷ \(\frac{10}{10}\)
= \(\frac{5}{10}\) ÷ \(\frac{5}{5}\)
= \(\frac{1}{2}\)
HOT Problems
Question 18.
Mathematical PRACTICE Stop and Reflect Write two fractions whose sum is greater than 1.
Answer:
Two fractions whose sum is greater than 1:
1. \(\frac{3}{2}\) + \(\frac{1}{2}\) = 2.
2. \(\frac{5}{6}\) + \(\frac{19}{6}\) = 4.
Explanation:
Two fractions whose sum is greater than 1:
1. \(\frac{3}{2}\) + \(\frac{1}{2}\) = [(3 + 1) ÷ 2]
= \(\frac{4}{2}\) ÷ \(\frac{2}{2}\)
= \(\frac{2}{1}\)
= 2.
2. \(\frac{5}{6}\) + \(\frac{19}{6}\) = [(5 + 19) ÷ 6]
= \(\frac{24}{6}\) ÷ \(\frac{6}{6}\)
= \(\frac{4}{1}\)
= 4.
Question 19.
Building on the Essential Question How can I add like fractions?
Answer:
Adding like fractions there are Three Simple Steps:
Step 1: Make sure the bottom numbers (the denominators) are the same.
Step 2: Add the top numbers (the numerators), put that answer over the denominator.
Step 3: Simplify the fraction (if possible)
Explanation:
Adding like fractions there are:
Make sure the bottom numbers (the denominators) are the same. Add the top numbers (the numerators), put that answer over the denominator. Simplify the fraction (if possible)
McGraw Hill My Math Grade 4 Chapter 9 Lesson 2 My Homework Answer Key
Practice
Find each sum. Write in simplest form.
Question 1.
\(\frac{2}{6}\) + \(\frac{3}{6}\) = ________________
Answer:
\(\frac{2}{6}\) + \(\frac{3}{6}\) = \(\frac{5}{6}\)
Explanation:
Sum of \(\frac{2}{6}\) and \(\frac{3}{6}\):
=> \(\frac{2}{6}\) + \(\frac{3}{6}\)
=> [(2 + 3) ÷ 6]
=> \(\frac{5}{6}\)
Question 2.
\(\frac{3}{8}\) + \(\frac{3}{8}\) = ________________
Answer:
\(\frac{3}{8}\) + \(\frac{3}{8}\) = \(\frac{3}{4}\)
Explanation:
Sum of \(\frac{3}{8}\) and \(\frac{3}{8}\):
=> \(\frac{3}{8}\) + \(\frac{3}{8}\)
=> [(3 + 3) ÷ 8]
=> \(\frac{6}{8}\) ÷ \(\frac{2}{2}\)
=> \(\frac{3}{4}\)
Question 3.
\(\frac{1}{4}\) + \(\frac{1}{4}\) = ________________
Answer:
\(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{1}{2}\)
Explanation:
Sum of \(\frac{1}{4}\) and \(\frac{1}{4}\):
=> \(\frac{1}{4}\) + \(\frac{1}{4}\)
=> [(1 + 1) ÷ 4]
=> \(\frac{2}{4}\) ÷ \(\frac{2}{2}\)
=> \(\frac{1}{2}\)
Question 4.
\(\frac{5}{12}\) + \(\frac{3}{12}\) = ________________
Answer:
\(\frac{5}{12}\) + \(\frac{3}{12}\) = \(\frac{2}{3}\)
Explanation:
Sum of \(\frac{5}{12}\) and \(\frac{3}{12}\):
=> \(\frac{5}{12}\) + \(\frac{3}{12}\)
=> [(5 + 3) ÷ 12]
=>\(\frac{8}{12}\) ÷ \(\frac{4}{4}\)
=> \(\frac{2}{3}\)
Find each sum. Write in simplest form.
Question 5.
\(\frac{3}{5}\) + \(\frac{1}{5}\) = ________________
Answer:
\(\frac{3}{5}\) + \(\frac{1}{5}\) = \(\frac{4}{5}\)
Explanation:
Sum of \(\frac{3}{5}\) and \(\frac{1}{5}\):
=> \(\frac{3}{5}\) + \(\frac{1}{5}\)
=> [(3 + 1) ÷ 5]
=> \(\frac{4}{5}\)
Question 6.
\(\frac{4}{10}\) + \(\frac{1}{10}\) = ________________
Answer:
\(\frac{4}{10}\) + \(\frac{1}{10}\) = \(\frac{1}{2}\)
Explanation:
Sum of \(\frac{4}{10}\) and \(\frac{1}{10}\):
=> \(\frac{4}{10}\) + \(\frac{1}{10}\)
=> [(4 + 1) ÷ 10]
=> \(\frac{5}{10}\) ÷ \(\frac{5}{5}\)
= \(\frac{1}{2}\)
Question 7.
\(\frac{1}{6}\) + \(\frac{3}{6}\) = ________________
Answer:
\(\frac{1}{6}\) + \(\frac{3}{6}\) = \(\frac{2}{3}\)
Explanation:
Sum of \(\frac{1}{6}\) and \(\frac{3}{6}\):
=> \(\frac{1}{6}\) + \(\frac{3}{6}\)
=> [(1 + 3) ÷ 6]
=> \(\frac{4}{6}\) ÷ \(\frac{2}{2}\)
=> \(\frac{2}{3}\)
Question 8.
\(\frac{50}{100}\) + \(\frac{30}{100}\) = ________________
Answer:
\(\frac{50}{100}\) + \(\frac{30}{100}\) = \(\frac{4}{5}\)
Explanation:
Sum of \(\frac{50}{100}\) and \(\frac{30}{100}\):
=> \(\frac{50}{100}\) + \(\frac{30}{100}\) =
=> [(50 + 30) ÷ 100]
= \(\frac{80}{100}\) ÷ \(\frac{10}{10}\)
=> \(\frac{8}{10}\) ÷ \(\frac{2}{2}\)
=> \(\frac{4}{5}\)
Problem Solving
Solve. Write the answer in simplest form.
Question 9.
Mathematical PRACTICE Use Number Sense It took Yuki \(\frac{1}{6}\) of an hour to water her flowers and \(\frac{4}{6}\) of an hour to weed her garden. What fraction of an hour did Yuki work in her yard?
Answer:
Fraction of an hour did Yuki work in her yard = \(\frac{5}{6}\)
Explanation:
Number of hours Yuki took to water her flowers = \(\frac{1}{6}\)
Number of hours Yuki took to weed her garden = \(\frac{4}{6}\)
Fraction of an hour did Yuki work in her yard = Number of hours Yuki took to water her flowers + Number of hours Yuki took to weed her garden
= \(\frac{1}{6}\) + \(\frac{4}{6}\)
= [(1 + 4) ÷ 6]
= \(\frac{5}{6}\)
Question 10.
Yesterday it rained \(\frac{5}{8}\) inch. Today it rained \(\frac{1}{8}\) inch. What is the total amount of rain for the two days?
Answer:
Total amount of rain for the two days = \(\frac{3}{4}\) inches.
Explanation:
Number of inches it rained Yesterday = \(\frac{5}{8}\)
Number of inches it rained Today = \(\frac{1}{8}\)
Total amount of rain for the two days = Number of inches it rained Yesterday + Number of inches it rained Today
= \(\frac{5}{8}\) + \(\frac{1}{8}\)
= [(5 + 1) ÷ 8]
= \(\frac{6}{8}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{4}\) inches.
Question 11.
Claudio walked \(\frac{3}{10}\) mile in the morning. He walked the same distance in the afternoon. How far did Claudio walk altogether?
Answer:
Number of miles Claudio walk altogether = \(\frac{3}{5}\)
Explanation:
Number of miles Claudio walked in the morning = \(\frac{3}{10}\)
He walked the same distance in the afternoon.
=> Number of miles Claudio walked in the afternoon = \(\frac{3}{10}\)
Number of miles Claudio walk altogether = Number of miles Claudio walked in the morning + Number of miles Claudio walked in the afternoon
= \(\frac{3}{10}\) + \(\frac{3}{10}\)
= [(3 + 3) ÷ 10]
= \(\frac{6}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{5}\)
Test Practice
Question 12.
Pierre has 12 packages to send. He sent 2 packages on Monday and 2 more packages on Tuesday. What fraction of the packages has Pierre sent so far?
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{8}{12}\)
(D) \(\frac{2}{3}\)
Answer:
Fraction of the packages has Pierre sent so far = \(\frac{1}{3}\)
(B) \(\frac{1}{3}\)
Explanation:
Number of packages to send Pierre has = 12.
Number of packages he sent on Monday = 2.
Number of packages he sent on Tuesday = 2.
Fraction of the packages has Pierre sent so far = (Number of packages he sent on Monday + Number of packages he sent on Tuesday) ÷ Number of packages to send Pierre has
= (2 + 2) ÷ 12
= 4 ÷ 12 or \(\frac{4}{12}\)
= \(\frac{4}{12}\) ÷ \(\frac{4}{4}\) = \(\frac{1}{3}\)