All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 9 Lesson 1 Use Models to Add Like Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 9 Lesson 1 Use Models to Add Like Fractions
A unit fraction has a numerator of 1. It is one of the equal parts of the whole. Fractions that have the same denominators are called like fractions. You can use models to add like fractions.
Build It
Abigail is playing a board game with her friends. There are 5 game pieces. There is a red piece, a blue piece, a yellow piece, a green piece, and a purple piece. What is the total fraction of the pieces that are yellow, green, or purple?
Find \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\).
1. Model three \(\frac{1}{5}\) fraction tiles.
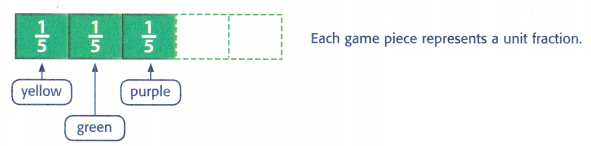

2. Add the like fractions.
There are three \(\frac{1}{5}\)-fraction tiles altogether.
So, \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) = \(\frac{3}{5}\). \(\frac{3}{5}\) is the sum of three unit fractions of \(\frac{1}{5}\).
So, the total fraction of game pieces that are yellow, green, or purple is ![]() .
.
Answer:
Total fraction of the pieces that are yellow, green, or purple = \(\frac{3}{5}\) 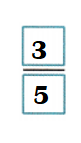
Explanation:
Total number of game pieces = 5.
Number of red pieces = 1.
Number of blue pieces = 1.
Number of yellow pieces = 1.
Fraction of yellow pieces = Number of yellow pieces ÷ Total number of game pieces
= 1 ÷ 5 or \(\frac{1}{5}\)
Number of green pieces = 1.
Fraction of green pieces = Number of green pieces ÷ Total number of game pieces
= 1 ÷ 5 or \(\frac{1}{5}\)
Number of purple pieces = 1.
Fraction of purple pieces = Number of purple pieces ÷ Total number of game pieces
= 1 ÷ 5 or \(\frac{1}{5}\)
Total fraction of the pieces that are yellow, green, or purple = Fraction of yellow pieces + Fraction of green pieces + Fraction of purple pieces
= \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
= [(1 + 1) ÷ 5] + \(\frac{1}{5}\)
= \(\frac{2}{5}\) + \(\frac{1}{5}\)
= [(2 + 1) ÷ 5]
= \(\frac{3}{5}\)
Not all fractions are unit fractions. You can decompose, or break down, a fraction into a sum of unit fractions.

Try It
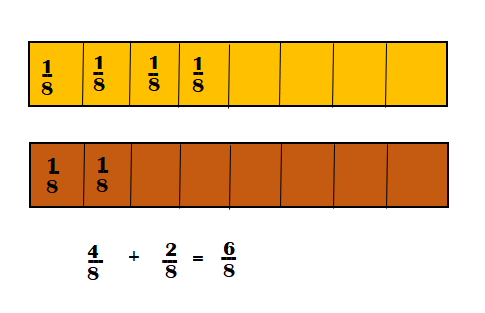
Find \(\frac{3}{8}\) + \(\frac{2}{8}\).
1. Model \(\frac{3}{8}\).

2. Model \(\frac{2}{8}\).

3. Add.
Count the total number of \(\frac{1}{8}\)-tiles. Notice that the parts being joined are part of the same whole, and each unit fraction is the same size.
There are ______________ \(\frac{1}{8}\)-tiles.
So, \(\frac{3}{8}\) + \(\frac{2}{8}\) = ![]() .
.
Answer:
Sum of \(\frac{3}{8}\) and \(\frac{2}{8}\) = 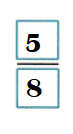
Explanation:
\(\frac{3}{8}\) = 
\(\frac{2}{8}\) = 
Total number of \(\frac{1}{8}\)-tiles = 8.
Sum of \(\frac{3}{8}\) + \(\frac{2}{8}\) = {(3 + 2) ÷ 8]
= \(\frac{5}{8}\)
Talk About It
Question 1.
Mathematical PRACTICE Identify Structure The fraction \(\frac{5}{8}\) can be considered as the sum of \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\). It can also be considered as the sum of \(\frac{3}{8}\) + \(\frac{2}{8}\). Write two other ways to think of \(\frac{5}{8}\) as a sum.
Answer:
One Way:
\(\frac{5}{8}\) = \(\frac{4}{8}\) + \(\frac{1}{8}\)
Second Way:
\(\frac{5}{8}\) = \(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{1}{8}\)
Explanation:
\(\frac{5}{8}\) = \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)
One Way:
\(\frac{5}{8}\) = \(\frac{4}{8}\) + \(\frac{1}{8}\)
= (4 + 1) ÷ 8
= \(\frac{5}{8}\)
Second Way:
\(\frac{5}{8}\) = \(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{1}{8}\)
= [(2 + 2) ÷ 8] + \(\frac{1}{8}\)
= \(\frac{4}{8}\) + \(\frac{1}{8}\)
= [(4 + 1) ÷ 8]
= \(\frac{5}{8}\)
Practice It
Model the sum using fraction tiles. Draw the model. Then add.
Question 2.
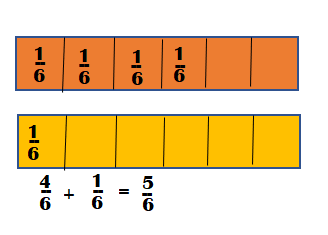
\(\frac{1}{6}\) + \(\frac{4}{6}\) = _________________
Answer:
Sum of \(\frac{1}{6}\) and \(\frac{4}{6}\) = \(\frac{5}{6}\)
Explanation:
Sum of \(\frac{1}{6}\) + \(\frac{4}{6}\) = (1 + 4) ÷ 6
= \(\frac{5}{6}\)
Question 3.
\(\frac{4}{8}\) + \(\frac{2}{8}\) = __________________
Answer:
Sum of \(\frac{4}{8}\) and \(\frac{2}{8}\) = \(\frac{6}{8}\)
Explanation:
Sum of \(\frac{4}{8}\) + \(\frac{2}{8}\) = (4 + 2) ÷ 8
= \(\frac{6}{8}\)
Use the table to answer Exercises 4 and 5.
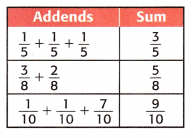
Question 4.
The table shows the sums of several like fractions. Study the pattern in the table.
Write a rule that you can use to add like fractions without using models.
Answer:
A rule that can be used to add like fractions without using models is that to add or subtract fractions they must have the same denominator (the bottom value).
Explanation:
To add or subtract fractions they must have the same denominator (the bottom value). If the denominators are already the same then it is just a matter of either adding or subtracting the numerators (the top value).
Question 5.
Use your rule from Exercise 4 to find \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\).
Answer:
Sum of \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)
Explanation:
Sum of \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
= [(1 + 1) ÷ 4] + \(\frac{1}{4}\)
= \(\frac{2}{4}\) + \(\frac{1}{4}\)
= [(2 + 1) ÷ 4
= \(\frac{3}{4}\)
Algebra Write each fraction as a sum of unit fractions. Then write an equation to decompose the fraction in a different way.
Question 6.
\(\frac{7}{8}\)
Answer:
\(\frac{7}{8}\) = \(\frac{4}{8}\) + \(\frac{3}{8}\) = \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{7}{8}\)
Explanation:
\(\frac{7}{8}\) = \(\frac{4}{8}\) + \(\frac{3}{8}\)
Decomposition:
\(\frac{7}{8}\) = \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{7}{8}\)
Question 7.
\(\frac{5}{10}\)
Answer:
\(\frac{5}{10}\) = \(\frac{3}{10}\) + \(\frac{2}{10}\) = \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)
Explanation:
\(\frac{5}{10}\) = \(\frac{3}{10}\) + \(\frac{2}{10}\)
Decomposition:
\(\frac{5}{10}\) = \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)
Apply It
Question 8.
Mathematical PRACTICE Use Number Sense Claire walked \(\frac{1}{3}\) mile on Saturday and \(\frac{1}{3}\) mile on Sunday. How many miles did she walk in all?
Answer:
Number of miles Claire walked in all = \(\frac{2}{3}\)
Explanation:
Number of miles Claire walked on Saturday = \(\frac{1}{3}\)
Number of miles Claire walked on Sunday = \(\frac{1}{3}\)
Number of miles Claire walked in all = Number of miles Claire walked on Saturday + Number of miles Claire walked on Sunday
= \(\frac{1}{3}\) + \(\frac{1}{3}\)
= (1 + 1) ÷ 3
= \(\frac{2}{3}\)
Question 9.
Miguel cut a cantaloupe into 8 slices. He ate 1 slice and his friends ate 4 slices. What fraction of the cantaloupe did they eat?
Answer:
Fraction of the cantaloupe did they eat = \(\frac{5}{8}\)
Explanation:
Number of slices Miguel cut a cantaloupe = 8.
Number of slices he ate = 1.
Number of slices his friends ate = 4.
Total number of slices they ate = Number of slices he ate + Number of slices his friends ate
= 1 + 4
= 5.
Fraction of the cantaloupe did they eat = Total number of slices they ate ÷ Number of slices Miguel cut a cantaloupe
= 5 ÷ 8 or \(\frac{5}{8}\)
Question 10.
There are 12 children at lunch. Six children are eating apples, four children are eating grapes, and two children are eating celery. What fraction of the children are eating fruit?
Answer:
Fraction of the children are eating fruit = \(\frac{10}{12}\)
Explanation:
Number of children at lunch = 12.
Number of children eating apples = 6.
Number of children eating grapes = 4.
Number of children eating celery = 2.
Total number of children eating fruits = Number of children eating apples + Number of children eating grapes
= 6 + 4
= 10.
Fraction of the children are eating fruit = Total number of children eating fruits ÷ Number of children at lunch
= 10 ÷ 12 or \(\frac{10}{12}\)
Question 11.
Mathematical PRACTICE Model Math Write three different ways to decompose \(\frac{9}{10}\) into a sum.
Answer:
Three different ways to decompose \(\frac{9}{10}\) into a sum:
\(\frac{9}{10}\) = \(\frac{5}{10}\) + \(\frac{4}{10}\)
\(\frac{9}{10}\) = \(\frac{3}{10}\) + \(\frac{5}{10}\) + \(\frac{1}{10}\)
\(\frac{9}{10}\) = \(\frac{7}{10}\) + \(\frac{2}{10}\)
Explanation:
Three different ways to decompose \(\frac{9}{10}\) into a sum:
\(\frac{9}{10}\) = \(\frac{5}{10}\) + \(\frac{4}{10}\)
\(\frac{9}{10}\) = \(\frac{3}{10}\) + \(\frac{5}{10}\) + \(\frac{1}{10}\)
= [(3 + 5) ÷ 10] + \(\frac{1}{10}\)
= + \(\frac{8}{10}\) + \(\frac{1}{10}\)
= (8 + 1) ÷ 10
= \(\frac{9}{10}\)
\(\frac{9}{10}\) = \(\frac{7}{10}\) + \(\frac{2}{10}\)
Write About It
Question 12.
When adding like fractions, why is the numerator the only part of the fraction that changes?
Answer:
When adding like fractions, the numerator is the only part of the fraction that changes because we add only numerators as denominators will be same.
Explanation:
Fractions with the same denominators are called like fractions.
To add two or more like fractions we simplify add their numerators. The denominator remains same. To subtract two or more like fractions we simply subtract their numerators and keep the same denominator.
McGraw Hill My Math Grade 4 Chapter 9 Lesson 1 My Homework Answer Key
Practice
Add.
Question 1.
\(\frac{1}{3}\) + \(\frac{1}{3}\) = ________________
Answer:
Sum of \(\frac{1}{3}\) and \(\frac{1}{3}\) = \(\frac{2}{3}\)
Explanation:
\(\frac{1}{3}\) + \(\frac{1}{3}\)
= (1 + 1) ÷ 3
= \(\frac{2}{3}\)
Question 2.
\(\frac{2}{12}\) + \(\frac{6}{12}\) = ________________
Answer:
Sum of \(\frac{2}{12}\) and \(\frac{6}{12}\) = \(\frac{8}{12}\)
Explanation:
\(\frac{2}{12}\) + \(\frac{6}{12}\)
= (2 + 6) ÷ 12
= \(\frac{8}{12}\)
Question 3.
\(\frac{3}{10}\) + \(\frac{4}{10}\) = ________________
Answer:
Sum of \(\frac{3}{10}\) and \(\frac{4}{10}\) = \(\frac{7}{10}\)
Explanation:
\(\frac{3}{10}\) + \(\frac{4}{10}\)
= (3 + 4) ÷ 10
= \(\frac{7}{10}\)
Question 4.
\(\frac{5}{8}\) + \(\frac{1}{8}\) = ________________
Answer:
Sum of \(\frac{5}{8}\) and \(\frac{1}{8}\) = \(\frac{6}{8}\)
Explanation:
\(\frac{5}{8}\) + \(\frac{1}{8}\)
= (5 + 1) ÷ 8
= \(\frac{6}{8}\)
Write an addition sentence for each model. Then find the sum.
Question 5.
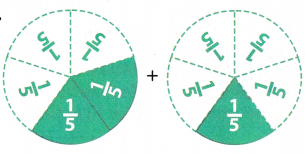
Answer:
Total number of shaded parts of the models = \(\frac{3}{5}\)
Explanation:
Number of shaded in first model = \(\frac{2}{5}\)
Number of shaded in second model = \(\frac{1}{5}\)
Total number of shaded parts of the models = Number of shaded in first model + Number of shaded in second model
= \(\frac{2}{5}\) + \(\frac{1}{5}\)
= (2 + 1) ÷ 5
= \(\frac{3}{5}\)
Question 6.
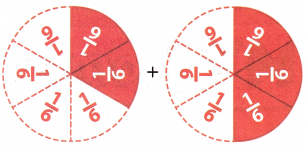
Answer:
Total number of shaded parts of the models = \(\frac{5}{6}\)
Explanation:
Number of shaded in first model = \(\frac{2}{6}\)
Number of shaded in second model = \(\frac{3}{6}\)
Total number of shaded parts of the models = Number of shaded in first model + Number of shaded in second model
= \(\frac{2}{6}\)+ \(\frac{3}{6}\)
= (2 + 3) ÷ 6
= \(\frac{5}{6}\)
Question 7.
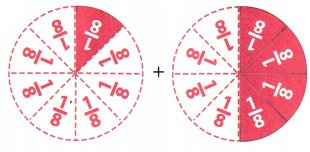
Answer:
Total number of shaded parts of the models = \(\frac{5}{8}\)
Explanation:
Number of shaded in first model = \(\frac{1}{8}\)
Number of shaded in second model = \(\frac{4}{8}\)
Total number of shaded parts of the models = Number of shaded in first model + Number of shaded in second model
= \(\frac{1}{8}\)+ \(\frac{4}{8}\)
= (1 + 4) ÷ 8
= \(\frac{5}{8}\)
Question 8.
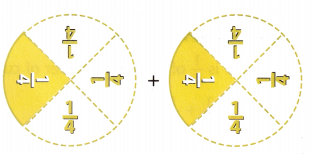
Answer:
Total number of shaded parts of the models = \(\frac{2}{4}\)
Explanation:
Number of shaded in first model = \(\frac{1}{4}\)
Number of shaded in second model = \(\frac{1}{4}\)
Total number of shaded parts of the models = Number of shaded in first model + Number of shaded in second model
= \(\frac{1}{4}\)+ \(\frac{1}{4}\)
= (1 + 1) ÷ 4
= \(\frac{2}{4}\)
Problem Solving
Question 9.
Mathematical PRACTICE Make Sense of Problems Nelson got a pack of 12 pencils. He took 3 pencils to put in his desk at school and 2 pencils to put in his locker at school. What is the fraction of total pencils that Nelson took to school?
Answer:
Fraction of total pencils that Nelson took to school = \(\frac{5}{12}\)
Explanation:
Number of pencils Nelson got a pack = 12.
Number of pencils Nelson took to put in his desk at school = 3.
Number of pencils Nelson took to put in his locker at school = 2.
Total number of pencils Nelson took = Number of pencils Nelson took to put in his desk at school + Number of pencils Nelson took to put in his locker at school
= 3 + 2
= 5.
Fraction of total pencils that Nelson took to school = Total number of pencils Nelson took ÷ Number of pencils Nelson got a pack
= 5 ÷ 12 or \(\frac{5}{12}\)
Question 10.
There are 10 chicks on Ginger’s farm. She has 2 chicks in one outdoor pen and 5 chicks in another. The rest of the chicks are in the barn. What is the fraction of total chicks in outdoor pens?
Answer:
Fraction of total chicks in outdoor pens = \(\frac{7}{10}\)
Explanation:
Number of chicks on Ginger’s farm = 10.
Number of chicks in one outdoor pen she has = 2.
Number of chicks in another she has = 5.
Number of chicks are in the barn = Number of chicks on Ginger’s farm – (Number of chicks in one outdoor pen she has + Number of chicks in another she has)
= 10 – (2 + 5)
= 10 – 7
= 3.
Total number of chicks in outdoor pens = Number of chicks in one outdoor pen she has + Number of chicks in another she has
= 2 + 5
= 7.
Fraction of total chicks in outdoor pens = Total number of chicks in outdoor pens ÷ Number of chicks on Ginger’s farm
= 7 ÷ 10 or \(\frac{7}{10}\)
Vocabulary Check
Question 11.
Explain what is the same about two fractions that are like fractions.
Answer:
Like fractions are the group of two or more fractions having the same denominator.
Explanation:
The group of two or more fractions that have exactly the same denominator are called like fractions. In these fractions, the whole is divided into a fixed number of equal portions. For example, 5/6 and 4/6 are like fractions. Here, we have divided the whole into 6 equal parts.