McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions

/ By

All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 9 Operations with Fractions will give you a clear idea of the concepts.

McGraw-Hill My Math Grade 4 Answer Key Chapter 9 Operations with Fractions

Essential Question
How can I use operations to model real-world fractions?
Answer:
I use operations to model real-world fractions for splitting a bill and calculating the discounted price of a object.

Explanation:
I use operations to model real-world fractions like:
Splitting a bill while eating at a restaurant.
Calculating the discounted price of an object on sale.

Am I Ready
Compare. Use <, >, or =.
Question 1.
\(\frac{1}{3}\) McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 1 \(\frac{1}{6}\)
Answer:
\(\frac{1}{3}\) < \(\frac{1}{6}\)

Explanation:
\(\frac{1}{3}\) = 1 out of 3.
\(\frac{1}{6}\) = 1 out of 6.
=> \(\frac{1}{3}\) is lesser than \(\frac{1}{6}\).

Question 2.
\(\frac{4}{5}\) McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 1 \(\frac{8}{10}\)
Answer:
\(\frac{4}{5}\) = \(\frac{8}{10}\)

Explanation:
\(\frac{4}{5}\) = 4 out of 5.
\(\frac{8}{10}\) =  \(\frac{8}{10}\) ÷  \(\frac{2}{2}\) =  \(\frac{4}{5}\)
=> \(\frac{4}{5}\) is same to \(\frac{8}{10}\).

Question 3.
\(\frac{2}{5}\) McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 1 \(\frac{2}{3}\)
Answer:
\(\frac{2}{5}\) < \(\frac{2}{3}\)

Explanation:
\(\frac{2}{5}\) = 2 out of 5.
\(\frac{2}{3}\) = 2 out of 3.
=> \(\frac{2}{5}\) is lesser than \(\frac{2}{3}\)

Question 4.
\(\frac{2}{10}\) McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 1 \(\frac{10}{100}\)
Answer:
\(\frac{2}{10}\) > \(\frac{10}{100}\)

Explanation:
\(\frac{2}{10}\) = \(\frac{2}{10}\) ÷ \(\frac{2}{2}\)  = \(\frac{1}{5}\) = 1 out of 5.
\(\frac{10}{100}\) = \(\frac{10}{100}\) ÷ \(\frac{10}{10}\)  = \(\frac{1}{10}\) = 1 out of 10.
=> \(\frac{2}{10}\) is greater than \(\frac{10}{100}\)

Question 5.
\(\frac{3}{5}\) McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 1 \(\frac{2}{8}\)
Answer:
\(\frac{3}{5}\) > \(\frac{2}{8}\)

Explanation:
\(\frac{3}{5}\) = 3 out of 5.
\(\frac{2}{8}\) = \(\frac{2}{8}\) ÷ \(\frac{2}{2}\)  = \(\frac{1}{4}\) = 1 out of 4.
\(\frac{3}{5}\) is greater than \(\frac{2}{8}\)

Question 6.
\(\frac{1}{4}\) McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 1 \(\frac{2}{8}\)
Answer:
\(\frac{1}{4}\) = \(\frac{2}{8}\)

Explanation:
\(\frac{1}{4}\) = 1 out of 4.
\(\frac{2}{8}\) = \(\frac{2}{8}\)  ÷ \(\frac{2}{2}\)  = \(\frac{1}{4}\) = 1 out of 4.
\(\frac{1}{4}\) is equal to \(\frac{2}{8}\).

Write each fraction in simplest form.
Question 7.
\(\frac{4}{6}\) _________________
Answer:
Simplest form of \(\frac{4}{6}\) = \(\frac{2}{3}\)

Explanation:
Simplest form:
\(\frac{4}{6}\) = \(\frac{4}{6}\) ÷ \(\frac{2}{2}\)  = \(\frac{2}{3}\)

Question 8.
\(\frac{6}{10}\) _________________
Answer:
Simplest form of \(\frac{6}{10}\) = \(\frac{3}{5}\)

Explanation:
Simplest form:
\(\frac{6}{10}\) = \(\frac{6}{10}\) ÷ \(\frac{2}{2}\)  = \(\frac{3}{5}\)

Question 9.
\(\frac{3}{12}\) _________________
Answer:
Simplest form of \(\frac{3}{12}\) = \(\frac{1}{4}\)

Explanation:
Simplest form:
\(\frac{3}{12}\) = \(\frac{3}{12}\) ÷ \(\frac{3}{3}\) = \(\frac{1}{4}\)

Question 10.
\(\frac{60}{100}\) _________________
Answer:
Simplest form of \(\frac{60}{100}\) = \(\frac{3}{5}\)

Explanation:
Simplest form:
\(\frac{60}{100}\) = \(\frac{60}{100}\) ÷ \(\frac{10}{10}\) = \(\frac{6}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{5}\)

Question 11.
\(\frac{5}{10}\) _________________
Answer:
Simplest form of \(\frac{5}{10}\) = \(\frac{1}{2}\)

Explanation:
Simplest form:
\(\frac{5}{10}\) = \(\frac{5}{10}\) ÷ \(\frac{5}{5}\) = \(\frac{1}{2}\)

Question 12.
\(\frac{4}{12}\) _________________
Answer:
Simplest form of \(\frac{4}{12}\) = \(\frac{1}{3}\)

Explanation:
Simplest form:
\(\frac{4}{12}\) = \(\frac{4}{12}\) ÷ \(\frac{4}{4}\) = \(\frac{1}{3}\)

Write an equivalent fraction.
Question 13.
\(\frac{1}{3}\) _________________
Answer:
Equivalent fraction of \(\frac{1}{3}\) = \(\frac{3}{9}\)

Explanation:
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{3}{3}\)  = \(\frac{3}{9}\)

Question 14.
\(\frac{3}{4}\) _________________
Answer:
Equivalent fraction of \(\frac{3}{4}\) = \(\frac{15}{20}\)

Explanation:
\(\frac{3}{4}\) = \(\frac{3}{4}\) × \(\frac{5}{5}\)  = \(\frac{15}{20}\)

Question 15.
\(\frac{7}{10}\) _________________
Answer:
Equivalent fraction of \(\frac{7}{10}\) = \(\frac{21}{30}\)

Explanation:
\(\frac{7}{10}\) = \(\frac{7}{10}\) × \(\frac{3}{3}\)  = \(\frac{21}{30}\)

Question 16.
\(\frac{3}{5}\) _________________
Answer:
Equivalent fraction of \(\frac{3}{5}\) = \(\frac{6}{10}\)

Explanation:
\(\frac{3}{5}\) = \(\frac{3}{5}\) × \(\frac{2{2}\) = \(\frac{6}{10}\)

Question 17.
\(\frac{2}{10}\) _________________
Answer:
Equivalent fraction of \(\frac{2}{10}\) = \(\frac{6}{30}\)

Explanation:
\(\frac{2}{10}\) = \(\frac{2}{10}\) ×\(\frac{3}{3}\) = \(\frac{6}{30}\)

Question 18.
\(\frac{90}{100}\) _________________
Answer:
Equivalent fraction of \(\frac{90}{100}\) = \(\frac{9}{10}\)

Explanation:
\(\frac{90}{100}\) = \(\frac{90}{100}\) × \(\frac{10}{10}\) = \(\frac{9}{10}\)

Question 19.
Hannah has a garden with basil, rosemary, and parsley. One sixth of her garden has basil. One half of her garden has rosemary. One-third of her garden has parsley. “Draw and label a picture of Hannah’s garden.
Answer:
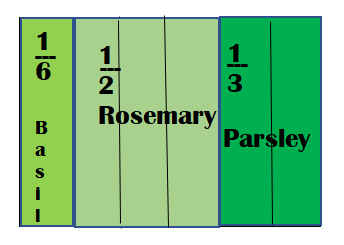
McGraw-Hill-My-Math-Grade-4-Answer-Key-Chapter-9-Operations-with-Fractions-19

Explanation:
Portion of her garden has basil = One sixth = \(\frac{1}{6}\)
Portion of her garden has rosemary = One half = \(\frac{1}{2}\)
Portion of her garden has parsley = One-third = \(\frac{1}{3}\)
Total parts = 6.

My Math Words
Review Vocabulary
denominator
mixed number
numerator simplest form

Making Connections
Write or draw an example and a non-example of each review vocabulary.
McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 2
Answer:
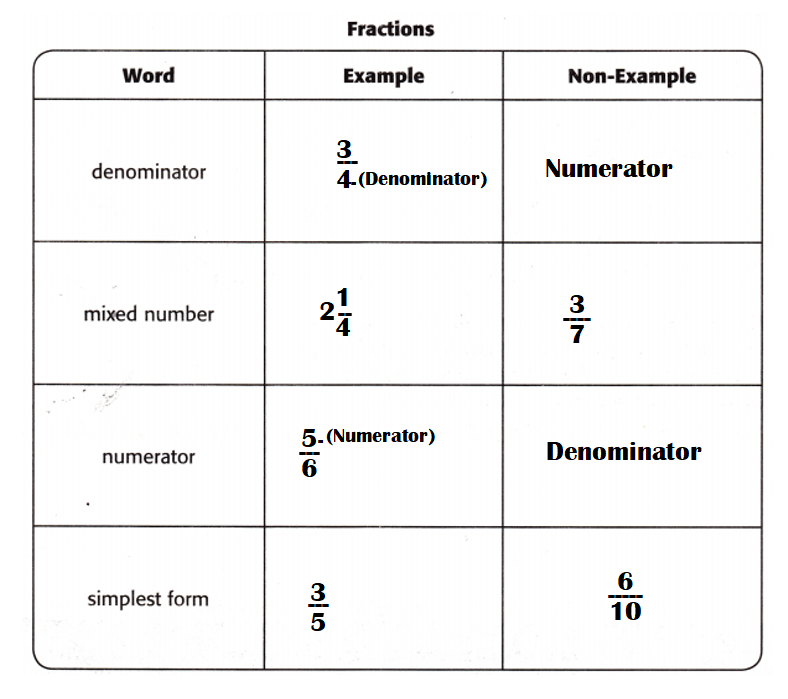
McGraw-Hill-My-Math-Grade-4-Answer-Key-Chapter-9-Operations-with-Fractions-Making Connections

Explanation:
Example of denominator = \(\frac{3}{4}\) – 4 is denominator.
Non-Example of denominator = Numerator.
Example of Mixed fraction = 2\(\frac{1}{4}\)
Non-Example of Mixed fraction = \(\frac{3}{7}\)
Example of Numerator = \(\frac{5}{6}\) – 5 is numerator.
Non-Example of Numerator = Denominator.
Example of Simplest form = \(\frac{3}{5}\)
Non-Example of Simplest form =\(\frac{6}{10}\)

My Vocabulary Cards

McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 3

Ideas for Use

  • Write a tally mark on each card every time you read the word in this chapter or use it in your writing. Challenge yourself to use at least 5 tally marks.
  • Ask students to use the blank cards to draw or write phrases or examples that will help them with concepts like adding like fractions and subtracting mixed numbers.

Fractions that have the same denominator. Like can mean “of the same form or kind.” How does this help you remember the meaning of like fractions.
Answer:
Fractions that have the same denominator are called like fractions.

Explanation:
Fractions with the same denominator are called like fractions.
Example: \(\frac{2}{5}\) \(\frac{3}{5}\) \(\frac{7}{5}\)

My Foldable
Follow the steps on the back to make your Foldable.
McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 4
McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 5
McGraw Hill My Math Grade 4 Chapter 9 Answer Key Operations with Fractions 6
Answer:
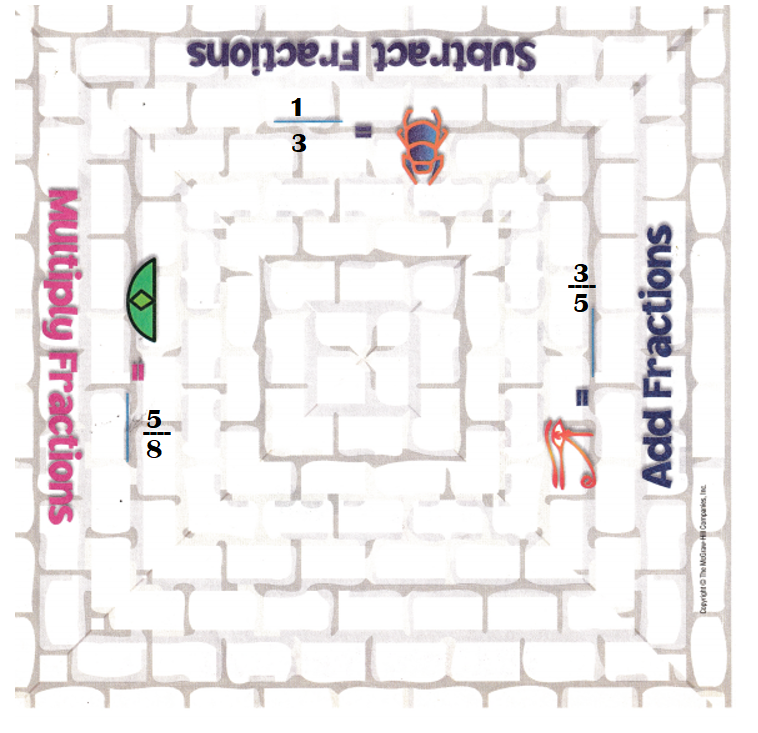
McGraw-Hill-My-Math-Grade-4-Answer-Key-Chapter-9-Operations-with-Fractions-My Foldable

Explanation:
Multiplication fraction = 5 × \(\frac{1}{8}\) = \(\frac{5}{8}\)
Addition fraction = \(\frac{1}{5}\) + \(\frac{2}{5}\) = (1 + 2) ÷ 5 = \(\frac{3}{5}\)
Subtraction fraction = \(\frac{5}{6}\) – \(\frac{3}{6}\) = (5 – 3) ÷ 6 = \(\frac{2}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{3}\)

Leave a Comment

Scroll to Top
Scroll to Top