All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 8 Review will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Chapter 8 Review Answer Key
Vocabulary Check
Question 1.
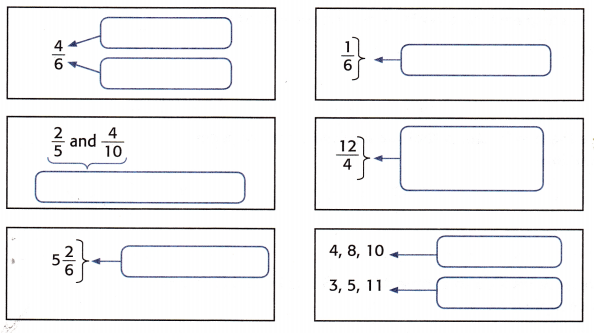
Use the words in the word bank to label each card.
composite
denominator
equivalent fractions
improper fraction
mixed number
numerator
prime
simplest form
Answer:
Explanation:
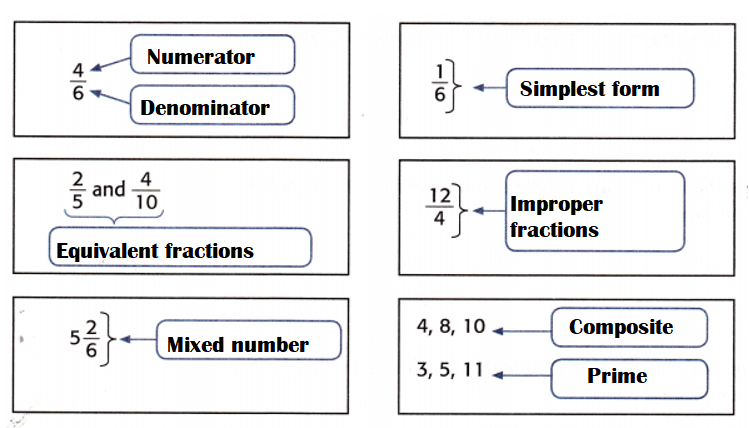
Composite – In Mathematics, composite are numbers that have more than two factors.
Denominator – The denominator of a fraction tells you how many parts a whole is broken into.
Equivalent fractions – Equivalent fractions are the fractions that have different numerators and denominators but are equal to the same value.
Improper fraction – An improper fraction is a fraction whose numerator is equal to or greater than its denominator.
Mixed number – A mixed number is a combination of a whole number and a fraction.
Numerator – The value placed above the horizontal line in a fraction is called a numerator.
Prime – A prime number is a whole number greater than 1 whose only factors are 1 and itself.
Simplest form – A fraction is in simplest form if the top and bottom have no common factors other than 1.
Write an example of each of the following words.
Question 2.
factor pairs __________________
Answer:
Examples for factor pairs:
6 × 3 = 18.
11 × 10 = 110.
Explanation:
Factors are often given as pairs of numbers, which multiply together to give the original number. These are called factor pairs.
Examples: 6 × 3 = 18.
11 × 10 = 110.
Question 3.
greatest common factor __________________
Answer:
The greatest common factor of 12 and 24 = 4.
Explanation:
The greatest common factor (GCF) of a set of numbers is the largest factor that all the numbers share.
Examples:
12 and 20.
Factors of 12:
1,2,3,4,6,12.
Factors of 20.:
1,2,4,5,10,20.
Question 4.
least common multiple __________________
Answer:
Least common multiple of 16 and 20 = 80.
Explanation:
LCM denotes the least common factor or multiple of any two or more given integers.
For example, L.C.M of 16 and 20
16 = 2 × 2 × 2 × 2
20 = 2 × 2 × 5
LCM of 16 and 20 = 2 x 2 x 2 x 2 x 5 = 80, where 80 is the smallest common multiple for numbers 16 and 20.
Question 5.
benchmark fractions __________________
Answer:
Benchmark numbers are numbers against which other numbers or quantities can be estimated and compared.
Explanation:
In math, benchmark fractions can be defined as common fractions that we can measure or judge against, when measuring, comparing, or ordering other fractions.
Concept Check
Find the factor pairs of each number.
Question 6.
52
_____________ and _______________
_____________ and _______________
_____________ and _______________
Answer:
Factor pairs of 52 are:
1 and 52.
2 and 26.
4 and 13.
Explanation:
Factor pairs of 52:
1 × 52 = 52.
2 × 26 = 52.
4 × 13 = 52.
Question 7.
36
_____________ and _______________
_____________ and _______________
_____________ and _______________
_____________ and _______________
_____________ and _______________
Answer:
Factor pairs of 36 are:
1 and 36.
2 and 18.
3 and 12.
4 and 9.
6 and 6.
Explanation:
Factors of 36:
1 × 36 = 36.
2 × 18 = 36.
3 × 12 = 36.
4 × 9 = 36.
6 × 6 = 36.
Question 8.
23
_____________ and _______________
Answer:
Factor pairs of 23 are:
1 and 23.
Explanation:
Factors of 23:
1 × 23 = 23.
Tell whether each number is prime, composite, or neither.
Question 9.
0 ________________
Answer:
0 is not a prime or composite number.
Explanation:
0 does not have a repeating decimal, it is a rational number.
Question 10.
31 ________________
Answer:
31 is a prime number.
Explanation:
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers.
Factors of 31:
1 × 31 = 31.
Question 11.
62 _________________
Answer:
62 is a composite number.
Explanation:
A composite number is a positive integer that can be formed by multiplying two smaller positive integers.
Factors of 62:
1 × 62 = 62.
2 × 31 = 62.
Circle the two fractions that are equivalent for each set of fractions.
Question 12.
\(\frac{3}{4}\) \(\frac{9}{12}\) \(\frac{2}{6}\)
Answer:
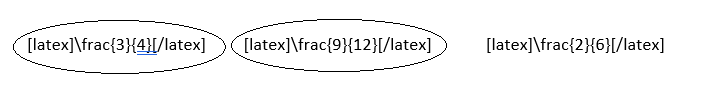
Explanation:
Simplest form:
\(\frac{3}{4}\) = \(\frac{3}{4}\)
\(\frac{9}{12}\) = \(\frac{9}{12}\) ÷ \(\frac{3}{3}\) = \(\frac{3}{4}\)
\(\frac{2}{6}\) = \(\frac{2}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{3}\)
The two fractions that are equivalent for each set of fractions:
\(\frac{3}{4}\) and \(\frac{9}{12}\)
Question 13.
\(\frac{4}{10}\) \(\frac{4}{100}\) \(\frac{40}{100}\)
Answer:
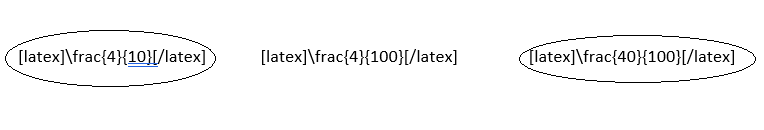
Explanation:
Simplest form:
\(\frac{4}{10}\) = \(\frac{4}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{5}\)
\(\frac{4}{100}\) = \(\frac{4}{100}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{50}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{25}\)
\(\frac{40}{100}\) = \(\frac{40}{100}\) ÷ \(\frac{10}{10}\) = \(\frac{4}{10}\)÷ \(\frac{2}{2}\) = \(\frac{2}{5}\)
The two fractions that are equivalent for each set of fractions:
\(\frac{4}{10}\) and \(\frac{40}{100}\)
Question 14.
\(\frac{3}{5}\) \(\frac{1}{4}\) \(\frac{6}{10}\)
Answer:
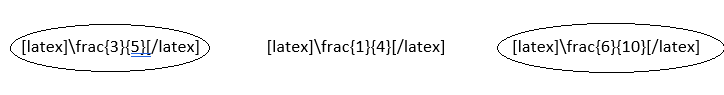
Explanation:
Simplest form:
\(\frac{3}{5}\) = \(\frac{3}{5}\)
\(\frac{1}{4}\) = \(\frac{1}{4}\)
\(\frac{6}{10}\) = \(\frac{6}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{5}\)
The two fractions that are equivalent for each set of fractions:
\(\frac{3}{5}\) and \(\frac{6}{10}\)
Write each fraction in simplest form. If it is in simplest form, write simplest form.
Question 15.
\(\frac{4}{10}\)
Answer:
Simplest form of \(\frac{4}{10}\) = \(\frac{2}{5}\)
Explanation:
Simplest form:
\(\frac{4}{10}\) = \(\frac{4}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{5}\)
Question 16.
\(\frac{3}{9}\)
Answer:
Simplest form of \(\frac{3}{9}\) = \(\frac{1}{3}\)
Explanation:
Simplest form:
\(\frac{3}{9}\) = \(\frac{3}{9}\) ÷ \(\frac{3}{3}\) = \(\frac{1}{3}\)
Question 17.
\(\frac{3}{10}\)
Answer:
Simplest form of \(\frac{3}{10}\) = \(\frac{3}{10}\) because its already in its simplest form.
Explanation:
Simplest form:
\(\frac{3}{10}\) = \(\frac{3}{10}\)
Compare. Use >, <, or =. Check your answer using fraction tiles or number lines.
Question 18.
\(\frac{5}{8}\) ![]() \(\frac{1}{3}\)
\(\frac{1}{3}\)
Answer:
\(\frac{5}{8}\) > \(\frac{1}{3}\)
Explanation:
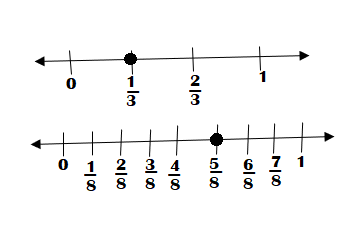
\(\frac{5}{8}\) is greater than \(\frac{1}{3}\)
Question 19.
\(\frac{1}{5}\) ![]() \(\frac{4}{6}\)
\(\frac{4}{6}\)
Answer:
\(\frac{1}{5}\) < \(\frac{4}{6}\).
Explanation:
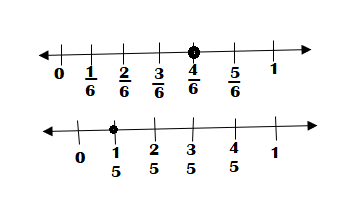
\(\frac{1}{5}\) is lesser than \(\frac{4}{6}\)
Question 20.
\(\frac{2}{3}\) ![]() \(\frac{8}{12}\)
\(\frac{8}{12}\)
Answer:
\(\frac{2}{3}\) < \(\frac{8}{12}\)
Explanation:
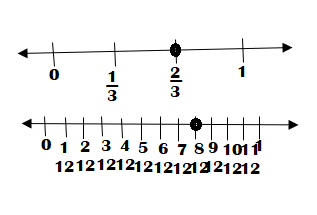
\(\frac{2}{3}\) is lesser than \(\frac{8}{12}\)
Problem Solving
Question 21.
Mrs. Evans has 13 pictures to hang on a wall. Is there any way she can arrange the pictures in rows other than 1 × 13 or 13 × 1, so that the same number of pictures is in each row? Tell whether 13 is a composite or prime number. Explain.
Answer:
No, Mrs. Evans cannot arrange the pictures in rows other than 1 × 13 or 13 × 1 because 13 is prime number.
Explanation:
Number of pictures to hang on a wall Mrs. Evans has = 13.
Factors of 13:
1 × 13 = 13.
Question 22.
There are \(\frac{2}{8}\) cup of peanuts and \(\frac{1}{4}\) cup of walnuts. Is there a greater amount of peanuts or walnuts? Explain.
Answer:
Both the amount of peanuts or walnuts are same.
Explanation:
Number of cup of peanuts = \(\frac{2}{8}\)
Number of cup of walnuts = \(\frac{1}{4}\)
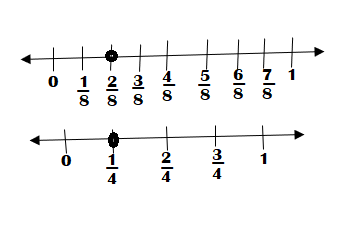
Both are same. They are equivalent fractions.
Question 23.
Mia has two whole bananas and one-fifth of another banana. Write a mixed number that represents the amount of bananas she has.
Answer:
Mixed number that represents the amount of bananas she has = 2\(\frac{1}{5}\)
Explanation:
Mia has two whole bananas and one-fifth of another banana.
Mixed number that represents the amount of bananas she has = 2 wholes + one-fifth
= 1 + 1 + \(\frac{1}{5}\)
= 2 + \(\frac{1}{5}\)
= 2\(\frac{1}{5}\)
Question 24.
Write a real-world problem to compare fractions.
Answer:
A real-world problem to compare fractions are a slice of watermelon and piece of pizza.
Explanation:
In real life, we will many examples of fractions, such as:
If a pizza is divided into two equal parts, then each part is equal to half of the whole pizza.
If we divide a slice of watermelon into three equal parts then each part is equal 1/3rd of the whole.
Test Practice
Question 25.
Which equation is true?

(A) 2\(\frac{2}{3}\) = 2 + 2 + 3
(B) 2\(\frac{2}{3}\) = 1 + 1 + 2 + 3
(C) 2\(\frac{2}{3}\) = 1 + 1 + \(\frac{1}{3}\) + \(\frac{1}{3}\)
(D) 2\(\frac{2}{3}\) = 1 + 1 + \(\frac{1}{3}\)
Answer:
Equation is true:
(C) 2\(\frac{2}{3}\) = 1 + 1 + \(\frac{1}{3}\) + \(\frac{1}{3}\)
Explanation:
(A) 2\(\frac{2}{3}\) = 2 + 2 + 3 (False)
(B) 2\(\frac{2}{3}\) = 1 + 1 + 2 + 3 (False)
(C) 2\(\frac{2}{3}\) = 1 + 1 + \(\frac{1}{3}\) + \(\frac{1}{3}\) (True)
(D) 2\(\frac{2}{3}\) = 1 + 1 + \(\frac{1}{3}\) (False)
=> 2\(\frac{2}{3}\) = 1 + 1 + \(\frac{1}{3}\) + \(\frac{1}{3}\)
Reflect
Use what you learned about fractions to complete the graphic organizer.
Reflect on the ESSENTIAL QUESTION Write your answer below.
Answer:
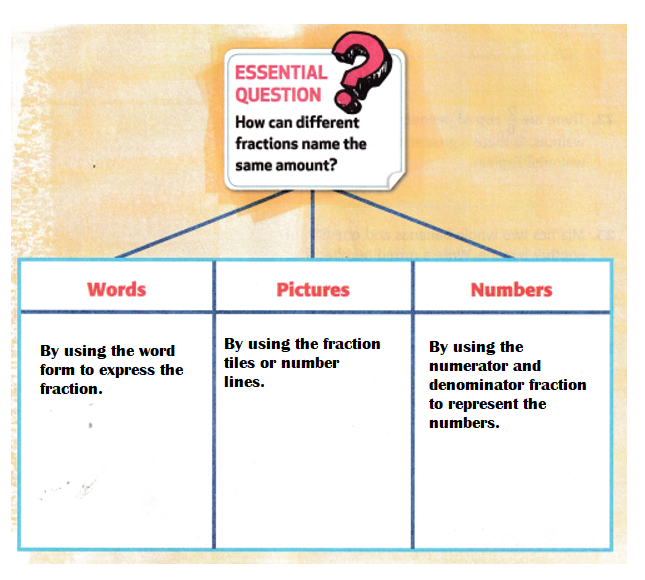
Explanation:
We can different fractions name the same amount by Equivalent fractions. They can be defined as fractions that may have different numerators and denominators but they represent the same value.