All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 8 Lesson 9 Mixed Numbers will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 8 Lesson 9 Mixed Numbers
A mixed number has a whole number part and a fraction part. It represents an amount greater than one whole.
There is more than 1 sandwich.
There are 1\(\frac{1}{2}\) sandwiches.
1 + \(\frac{1}{2}\) = 1\(\frac{1}{2}\)
The line is more than 2 inches long.
The line is 2\(\frac{1}{2}\) inches long.
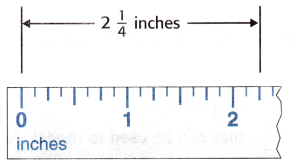
1 + 1 + \(\frac{1}{4}\) = 2\(\frac{1}{4}\)
Answer:
Total length of sandwiches = 2\(\frac{1}{4}\) inches.
Explanation:
A mixed number has a whole number part and a fraction part.
There is more than 1 sandwich.
There are 1\(\frac{1}{2}\) sandwiches.
=> 1 + \(\frac{1}{2}\) = 1\(\frac{1}{2}\)
The Length of sandwich is more than 2 inches long.
The line is 2\(\frac{1}{2}\) inches long.
=> 1 + 1 + \(\frac{1}{4}\) = 2\(\frac{1}{4}\)
Math in My World
Example 1
Caden had 3 apples. He cut off half of an apple to eat. What mixed number represents the amount of apples left?
Count the wholes. Then count the parts.
There are 2 whole apples and \(\frac{1}{2}\) of an apple left.
1 + 1 + \(\frac{1}{2}\) = 2\(\frac{1}{2}\)
So,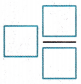 
of the apples are left.
Answer:
Amount of apples left = \(\frac{5}{2}\) or 2\(\frac{1}{2}\)
So,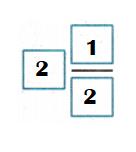
of the apples are left.
Explanation:
Number of apples Caden had = 3.
He cut off half of an apple to eat.
=>Amount of apples he cuts = \(\frac{1}{2}\)
Amount of apples left = Number of apples Caden had – Amount of apples he cuts
= 3 – \(\frac{1}{2}\)
= [(3 × 2) – 1] ÷ 2
= (6 – 1) ÷ 2
= \(\frac{5}{2}\) or 2\(\frac{1}{2}\)
OR
Amount of apples left = 1 + 1 + \(\frac{1}{2}\)
= 2 + \(\frac{1}{2}\)
= 2\(\frac{1}{2}\)
You can decompose a mixed number into a sum of whole numbers and unit fractions. Recall that a unit fraction is a fraction with a numerator of 1.
Example 2
Write the length of this leaf as a mixed number. Write an equation to show the mixed number.
1. Count the parts
The leaf is of an inch longer than 3 inches.
2. Count of parts.
The leaf is \(\frac{3}{4}\) of an inch longer than 3 inches.
3. Write the mixed number.
The leaf is 3\(\frac{3}{4}\) inches long.
4. Write the equation.
Three \(\frac{1}{4}\) – tiles can be used to model \(\frac{3}{4}\).
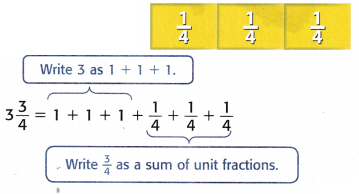
So, 3\(\frac{3}{4}\) = 1 + ____________ + 1 + \(\frac{1}{4}\) + \(\frac{1}{4}\) + _____________.
Answer:
Mixed fraction of length of leaf = 3\(\frac{3}{4}\) = 1 + 1 + 1 + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
Explanation:
Length of the leaf = 3\(\frac{3}{4}\)
Equation:
Mixed fraction:
Length of the leaf = 1 + 1 + 1 + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
= 2 + 1 + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
= 3 + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
= 3\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
= 3\(\frac{1}{2}\) + \(\frac{1}{4}\)
= 3\(\frac{3}{4}\) inches
Talk Math
How are fractions and mixed numbers alike? How are they different?
Answer:
Fractions and mixed numbers are alike as represent amounts that are greater than 1 and are different because a fraction is represented with its quotient and the remainder is a mixed fraction.
Explanation:
Improper fractions and mixed numbers are alike because both represent amounts that are greater than 1.
Improper fractions and mixed numbers are different because a fraction is represented with its quotient and remainder is a mixed fraction.
Guided Practice
Question 1.
Write a mixed number for the shaded model.
Answer:
Mixed fraction of shaded parts in the model = 2\(\frac{5}{6}\)
Explanation:
Total number of parts in a model = 6.
Number of shaded parts in the model = 1 + 1 + \(\frac{5}{6}\).
= 1 + 1 + \(\frac{5}{6}\)
= 2 + \(\frac{5}{6}\)
= 2\(\frac{5}{6}\)
Independent Practice
Write a mixed number for each shaded model.
Question 2.
Answer:
Mixed fraction of shaded parts in the model = 1\(\frac{2}{5}\)
Explanation:
Total number of parts = 5.
Number of shaded parts in the model = 1 + \(\frac{2}{5}\)
= 1\(\frac{2}{5}\)
Question 3.
Answer:
Mixed fraction of shaded parts in the model = 2\(\frac{5}{6}\)
Explanation:
Total number of parts = 6.
Number of shaded parts in the model = 1 + 1 + \(\frac{5}{6}\)
= 2 + \(\frac{5}{6}\)
= 2\(\frac{5}{6}\)
Question 4.
Answer:
Mixed fraction of shaded parts in the model = 2\(\frac{4}{8}\)
Explanation:
Total number of parts = 8.
Number of shaded parts in the model = 1 + 1 + \(\frac{4}{8}\)
= 2 + \(\frac{4}{8}\)
= 2\(\frac{4}{8}\)
Question 5.
Answer:
Mixed fraction of shaded parts in the model = 2\(\frac{11}{12}\)
Explanation:
Total number of parts = 12.
Number of shaded parts in the model = 1 + 1 + \(\frac{11}{12}\)
= 2 + \(\frac{11}{12}\)
= 2\(\frac{11}{12}\)
Question 6.
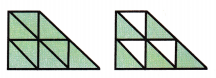
Answer:
Mixed fraction of shaded parts in the model = 1\(\frac{5}{8}\)
Explanation:
Total number of parts = 8.
Number of shaded parts in the model = 1 + \(\frac{5}{8}\)
= 1\(\frac{5}{8}\)
Question 7.
Answer:
Mixed fraction of shaded parts in the model = 2\(\frac{3}{4}\)
Explanation:
Total number of parts = 4.
Number of shaded parts in the model = 1 + 1 + \(\frac{3}{4}\)
= 2 + \(\frac{3}{4}\)
= 2\(\frac{3}{4}\)
Algebra Write an equation that represents each mixed number as a sum of whole numbers and unit fractions.
Question 8.
3\(\frac{1}{4}\) = ____________ + _____________ + _____________ + _______________
Answer:
Equation of 3\(\frac{1}{4}\) = 1 + 1 + 1 + \(\frac{1}{4}\)
Explanation:
Fraction given = 3\(\frac{1}{4}\):
= 3 wholes + \(\frac{1}{4}\)
= 1 + 1 + 1 + \(\frac{1}{4}\)
Question 9.
5\(\frac{1}{2}\) = _____________ + _____________ + _____________ + _____________ + _____________ + _____________
Answer:
Equation of 5\(\frac{1}{2}\) = 1 + 1 + 1 + 1 + 1 + \(\frac{1}{2}\)
Explanation:
Fraction given = 5\(\frac{1}{2}\):
= 5 wholes + \(\frac{1}{2}\)
= 1 + 1 + 1 + 1 + 1 + \(\frac{1}{2}\)
Question 10.
2\(\frac{2}{3}\) = ____________ + _____________ + _____________ + _______________
Answer:
Equation of 2\(\frac{2}{3}\) = 1 + 1 + \(\frac{2}{3}\)
Explanation:
Fraction given = 2\(\frac{2}{3}\):
= 2 wholes + \(\frac{2}{3}\)
= 1 + 1 + \(\frac{2}{3}\)
Question 11.
4\(\frac{3}{8}\) = ____________ + ____________ + ____________ + ____________ + ____________ + ____________ + ____________
Answer:
Equation of 4\(\frac{3}{8}\) = 1 + 1 + 1 + 1 + \(\frac{3}{8}\)
Explanation:
Fraction given = 4\(\frac{3}{8}\)
= 4 wholes + \(\frac{3}{8}\)
= 1 + 1 + 1 + 1 + \(\frac{3}{8}\)
Problem Solving
Question 12.
Mathematical PRACTICE Model Math Alex has one whole orange and one-fourth of a second orange. Write a mixed number that represents the amount of oranges he has.
Answer:
Mixed fraction that represents the amount of oranges he has = 1\(\frac{1}{4}\)
Explanation:
Alex has one whole orange and one-fourth of a second orange.
Mixed fraction that represents the amount of oranges he has = 1 whole + \(\frac{1}{4}\)
=> 1 + \(\frac{1}{4}\)
=> 1\(\frac{1}{4}\)
Question 13.
Brooke gave her dog two whole dog biscuits and a half of a third dog biscuit. Write a mixed number that represents the amount of dog biscuits she gave her dog.
Answer:
Mixed number that represents the amount of dog biscuits she gave her dog = 2\(\frac{2}{3}\)
Explanation:
Brooke gave her dog two whole dog biscuits and a half of a third dog biscuit.
Amount of dog biscuits she gave her dog = 2 wholes + half of a third
= 1 + 1 + \(\frac{2}{3}\)
= 2 + \(\frac{2}{3}\)
= 2\(\frac{2}{3}\)
Question 14.
There are three cans of Juice in the refrigerator and three-fourths of a fourth can. Write a mixed number that represents the amount of juice in the refrigerator.
Write an equation that represents this mixed number as a sum of whole numbers and unit fractions.
Answer:
Mixed number that represents the amount of juice in the refrigerator = 3\(\frac{3}{4}\)
Equation = 1 + 1 + 1 + \(\frac{3}{4}\) = 3\(\frac{3}{4}\)
Explanation:
There are three cans of Juice in the refrigerator and three-fourths of a fourth can.
Amount of juice in the refrigerator = 3 whole + three-fourths
= 1 + 1 + 1 + \(\frac{3}{4}\)
= 2 + 1 + \(\frac{3}{4}\)
= 3 + \(\frac{3}{4}\)
= 3\(\frac{3}{4}\)
HOT Problem
Question 15.
Mathematical PRACTICE Reason Write a mixed number that is greater than 3 and less than 4.
Answer:
Mixed number that is greater than 3 and less than 4 = 3\(\frac{1}{4}\)
Explanation:
Mixed number that is greater than 3 and less than 4:
=> 3 wholes + \(\frac{1}{4}\)
=> 3\(\frac{1}{4}\)
Question 16.
Building on the Essential Question How are mixed numbers used in the real world?
Answer:
Mixed numbers used in the real world is that serving a pizza.
Explanation:
Mixed numbers are used in the real world by expressing the parts of a whole as mixed fractions while serving a pizza or a pie at home.